Периодическая система машинного обучения

В MIT создали первую “периодическую таблицу” методов машинного обучения ^[1], при которых в исходных данных не задаются конкретные признаки (representation learning). Оказывается, многие (а может оказаться, что и все) методы, даже совсем друг на друга не похожие, сводятся по существу к одной и той же формуле. Причем не слишком сложной по своей форме. Работу ^[2]представили в конце апреля на конференции ICLR 2025.

“Обучение представлениям” или “обучение признакам”, или “обучение представлений”, — кажется, в русскоязычной ML-среде нет единого устоявшегося термина, так что будем использовать понятный “representation learning”. До появления representation learning для создания модели нужно было вручную выделить признаки данных, по которым модель будет обучаться и делать прогнозы. Для задач попроще и попонятнее это рабочая схема, но для сложных задач обработки текста и изображений она практически не применима. Выделить вручную признаки, по которым можно определить, что на картинке изображён, например, кот, а не цветок — задача нетривиальная. Человек с этим справляется слабо, поэтому возникла идея отдать поиск определяющих признаков на откуп машине — пусть модель сама определяет, какие параметры будут ключевыми. Этот переход к representation learning стал одной из фундаментальных основ, которые потом привели к прорывному развитию ML.

За прошедшие десятилетия накопилось огромное множество техник на основе representation learning, которые используют разные архитектуры и вид. А в последние годы новые способы появляются чуть ли не каждый день. Какие-то приспособлены под конкретные задачи, другие более универсальные. В каких-то прослеживается схожесть, другие выглядят принципиально новыми. Понять, чем они действительно схожи и различны, — задача во-первых просто интересная, а во-вторых и очень важная, так как это поможет эффективнее применять различные техники.

Существует много работ, где находятся взаимосвязи 2–3 техник, но авторы из MIT решили пойти дальше и объединили в один математический фреймворк 23 метода, причём совершенно разных: с учителем, без учителя и self-supervised.

Оказалось, что во всех них по существу происходит минимизация одной и той же функции потерь. Точнее, для всех этих методов функцию потерь можно привести к одному и тому же виду.

Сначала покажем саму обобщающую формулу, которую авторы назвали I-Con:

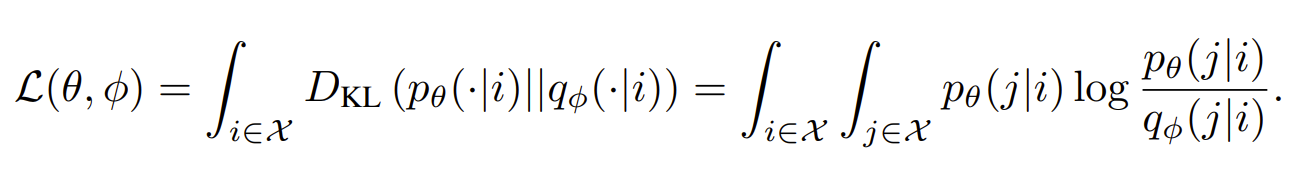
А теперь разберём её смысл. Суть этой функции потерь в DKL — расстоянии Кульбака–Лейблера, которое определяет, насколько вероятностное распределение q “удалено” от распределения p. Название “расстояние” в данном случае немного не соответствует привычному пониманию. Функционал DKL несимметричен — расстояние от p до q не будет равно расстоянию от q до p. Можно понимать это как расхождение или как относительное расстояние, то есть отличие тестируемого распределения q относительно некоторого эталонного, истинного p. Изначально расстояние Кульбака–Лейблера появилось в теории информации и нужно было, чтобы определить, сколько лишней информации мы потратим, если применим для кодирования q вместо p. Отсюда и несимметричность.

Но вернёмся к машинному обучению. Пусть есть некоторое множество данных, например, набор картинок. Эталонное распределение p — это как раз “учитель” — оно показывает, с какой вероятностью одна картинка должна привести к другой. Это может быть что угодно — простое гауссово распределение, задание классов картинок (“коты”, “цветы”), задание набора разных ракурсов одной и той же картинки и так далее. Относительно этого эталона мы будем оценивать распределение q, которое и будет определять взаимосвязь тех самых признаков (representations).

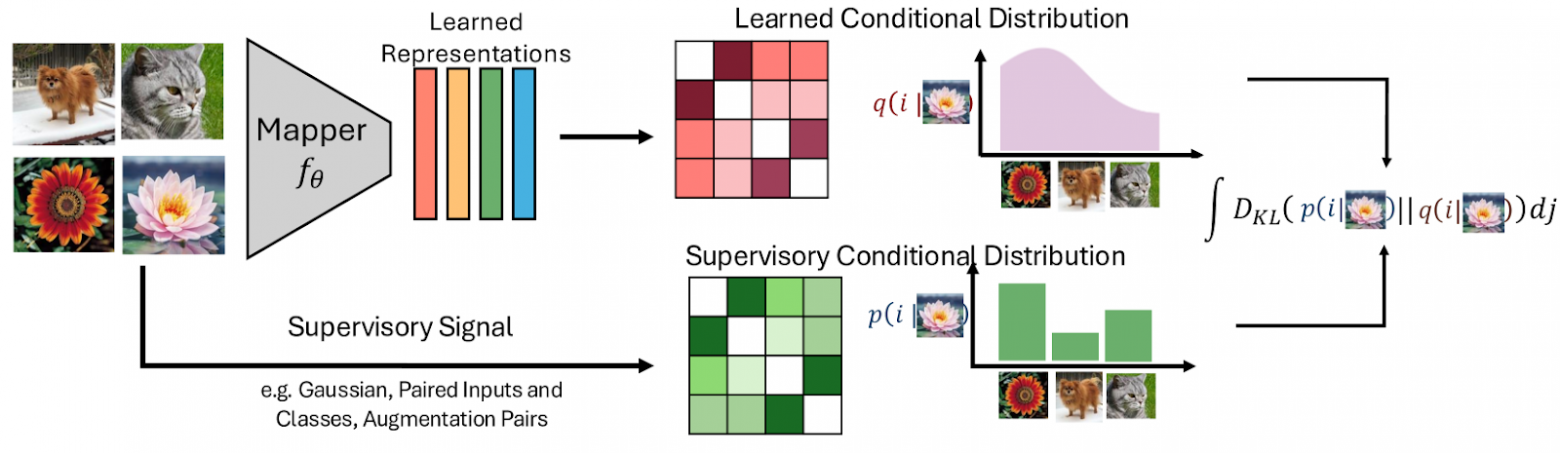
То распределение, которое даст наименьшее DKL по сравнению с p, будет считаться наиболее правильным.

Несмотря на формальную простоту, уравнение обобщает многие существующие методы. Оказывается, все они являются частными случаями функции потерь DKL с точностью до выбора p и q. Распределения p и q становятся своего рода координатами, а разные методы становятся точками на пересечении этих координат. В итоге получается периодическая система методов representation learning.

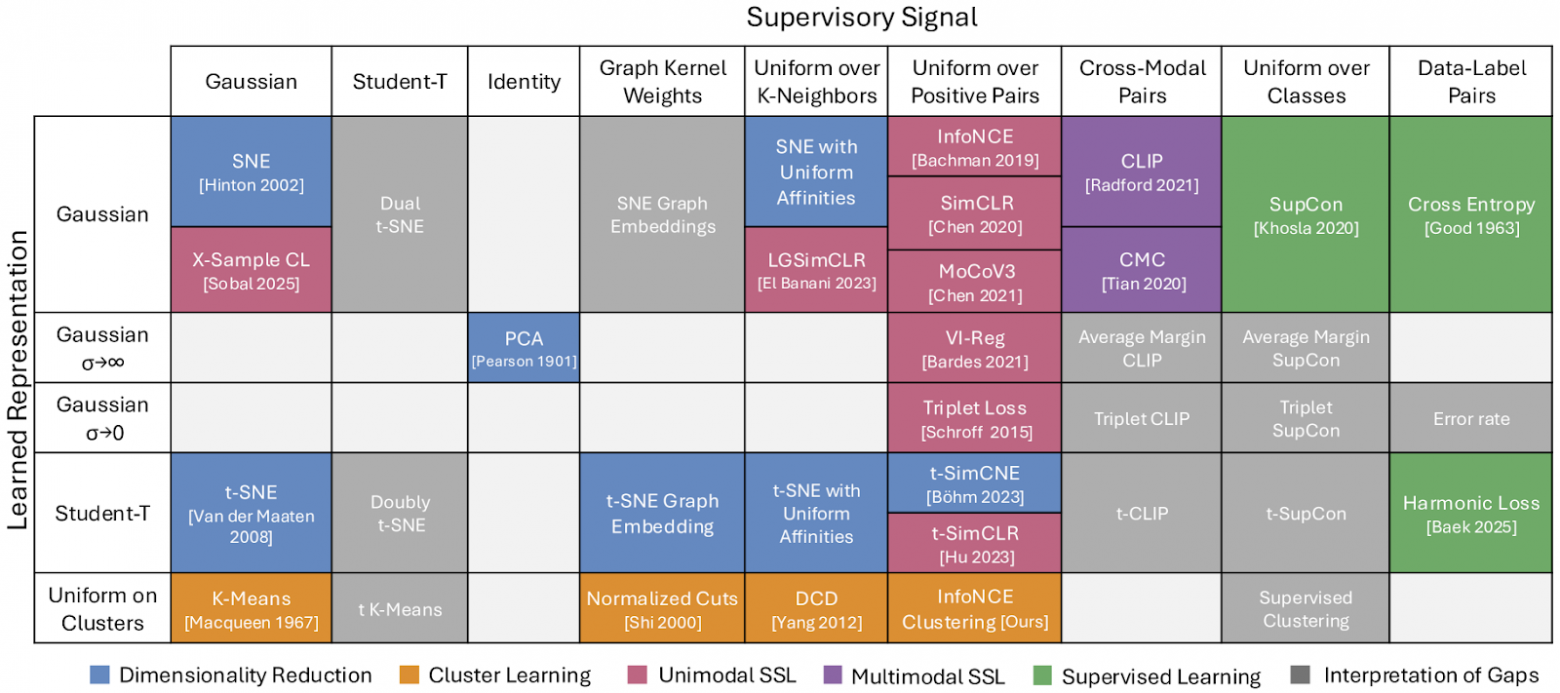
Например, модель InfoNCE использует в качестве обучающего датасета набор искажённых, отражённых и всякими другими способами изменённых версий одной и той же картинки (“uniform over positive pairs” по горизонтальной оси), а признаки определяются простым Гауссом (Gaussian по вертикальной оси). Авторы MIT проанализировали 23 работы и последовательно доказали, что все они сводятся к одной и той же формуле, только с разными p и q. Всего 15 теорем, в некоторых случаях доказательство тривиальное и прямо следует из исходного определения функции потерь, некоторые — гораздо более изощрённые.

Для примера возьмем тот же InfoNCE ^[3]. Обучающий набор — размеченное множество вариантов одной и той же картинки. 

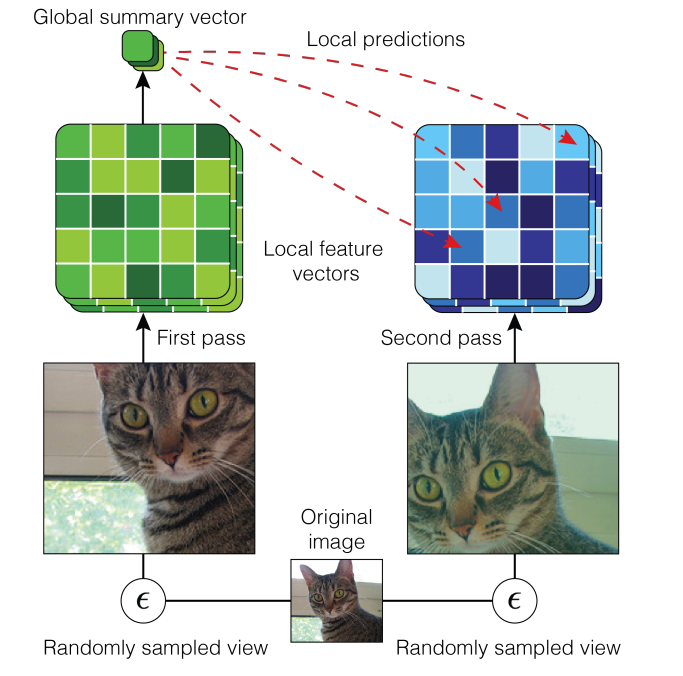
Поэтому, если для каждой картинки i есть k вариантов, то распределение p для каждой картинки j будет равно 1/k, если это вариация картинки i, и 0, если нет.

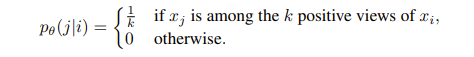
Обучаемое распределение q основано на сходствах между эмбеддингами картинок i и j — f(xi) и f(xj):

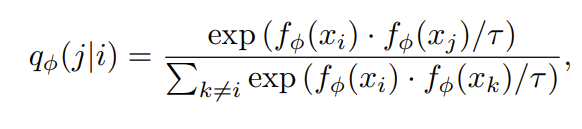
𝜏 — здесь просто параметр, который авторы называют температурой. А функция потерь определяется соответственно как

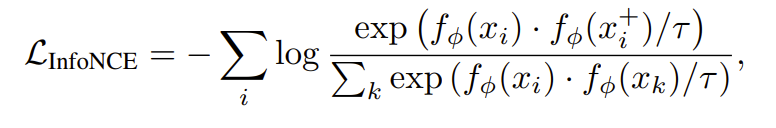
Это в точности равно перекрестной энтропии (количеству информации, нужному, чтобы описать событие с помощью распределения q вместо p). Так как в данном случае распределение p фиксированное, то минимизация перекрестной энтропии в точности эквивалентна минимизации  DKL   ( ее можно определить как разность между перекрестной энтропией и энтропией эталонного p). В итоге InfoNCE является частным случаем I-Con.

Теперь пару менее строгих примеров (в статье есть строгие доказательства и для них). Stochastic Neighbor Embedding (SNE) — классический пример подхода “соседи остаются соседями”. Изначальное распределение p можно представить в виде гауссова распределения, то есть каждая точка обучающего датасета “размазана” гауссом, чтобы определить соседство с другими точками. Итоговое распределение, которое обычно задается на пространстве меньшей размерности, тоже задается гауссовым размазыванием эмбеддинга каждой точки. 

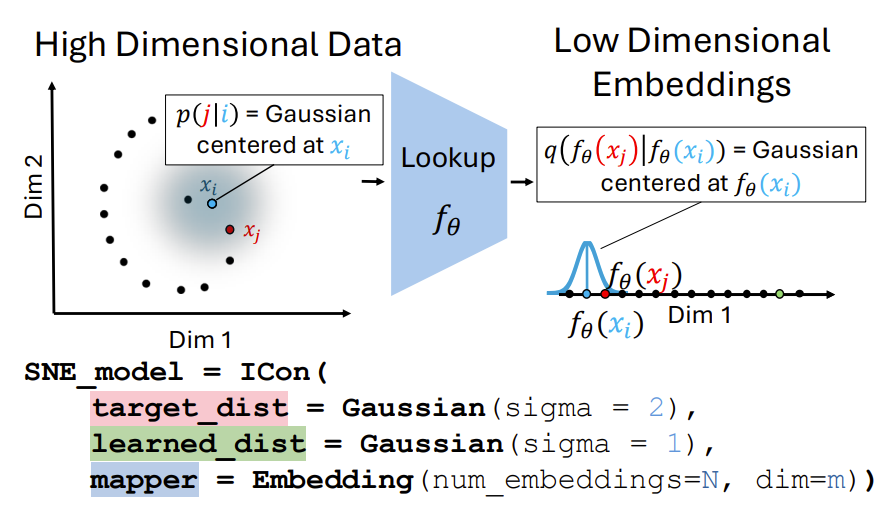
Разбиение на кластеры тоже сводится к I-con. Для подходов K-Means и DSD  распределение p это снова Гаусс, а q отражает являются ли эмбеддинги соседями по кластерам. 

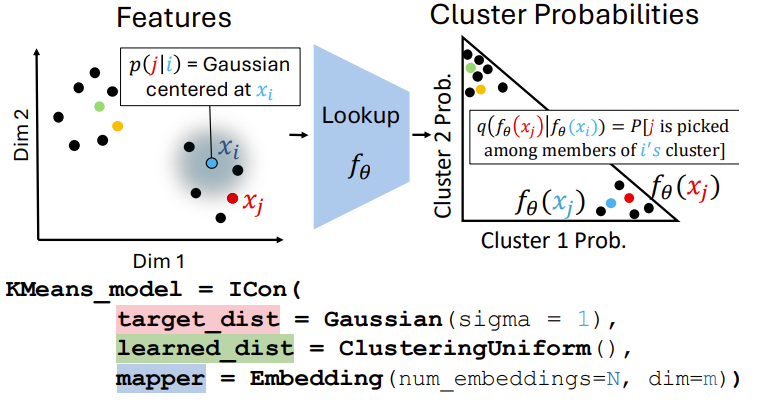
В получившейся “периодической таблице” заполнены не все ячейки, прямо как и в таблице Менделеева. Для некоторых из них (закрашены серым) авторы предлагают свои интерпретации, например, модель, которая будет использовать в качестве обучающего набора размеченные пары, а в качестве q — распределение гаусса с малой дисперсией, будет моделью “частоты ошибок”. 

Ту ячейку, которая показалась авторам наиболее перспективной, они заполнили самостоятельно и создали модель InfoNCE Clustering. Там, в отличие от простого InfoNCE, гауссово распределение заменяется на взвешенное k-ближайших соседей. На ImageNet-1K результат на 8% превзошел предыдущий state-of-the-art среди моделей без учителя. 

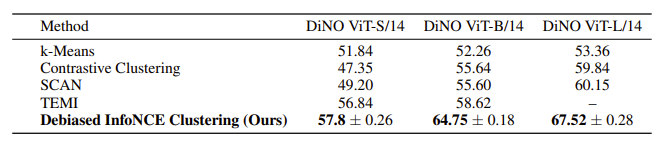
Авторы призывают читателей дополнять результаты другими моделями, которые они пока не успели рассмотреть. Само по себе объединение разных методов в принципиально единственный — уже теоретически важно. Но гораздо важнее, что это не просто объединение, а и некоторая структуризация, которая сразу же показывает белые пятна и указывает куда копать. Химию это привело к большим прорывам и процветанию, может и в этом случае окажется так же. 

Больше наших обзоров AI‑статей — на канале Pro AI. ^[4]