Часть 4: Mamba — State Space Models vs трансформеры

Обо мне

Привет, меня зовут Василий Техин. За последние 6 лет я прошёл путь от новичка в ML который ни в чем не разбирается, до человека, который может помочь разобраться другим не используя сложной математике ^[1] и приправляя обьяcнение наглядными примерами. В этой серии статей я разбираю прорывные модели “на пальцах”:

1. ResNet-18 — Архитектура, покорившая глубину ^[2]

2. Vision Transformer (ViT) — Когда трансформеры научились видеть ^[3]

3. Diffusion Transformer (DiT) — Stable Diffusion 3 как она есть ^[4] Сегодня: Mamba — революция в обработке длинных последовательностей!

---

Пролог: Почему Mamba?

Представьте тусовку ученых исследователей, где каждый должен переговорить со всеми. Для 10 человек — 100 диалогов (да, мы считаем, что разговоры первый со вторым и второй с первым отличаются и да да мы будем считать, что он и сам с собой говорит, кто поймет этих ученых!). Для 1000 — 1 000 000! Это квадратичная сложность (O(n²)) внимания ^[5] в трансформерах.
Mamba (State Space Models) решает это:

• Замена внимания на линейную рекуррентную сеть (O(n)).

• Селективность: динамический выбор важной информации.

• Ускорение в 5 раз на длинных текстах.

---

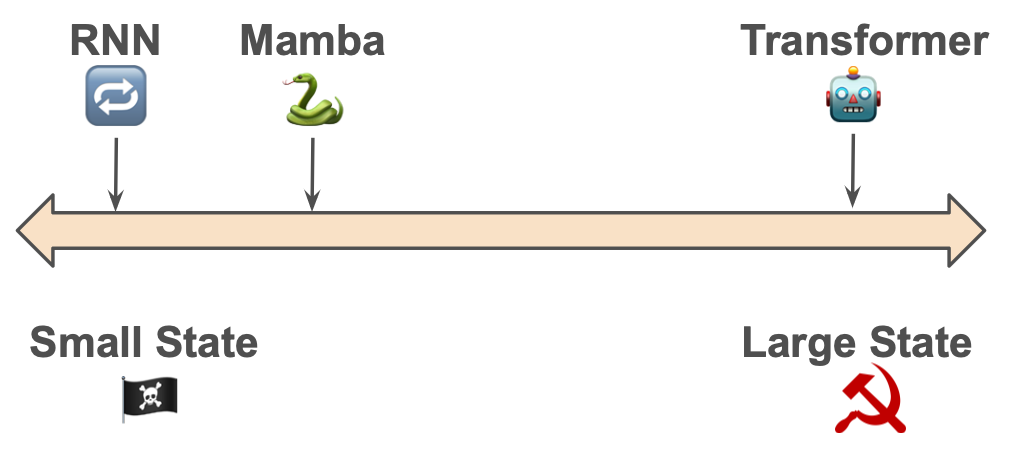
Ключевые компоненты Mamba

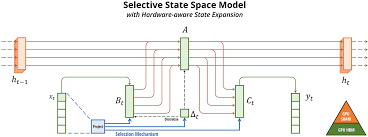
1. State Space Models (SSM)

State Space Models (SSM) — семейство линейных моделей для последовательностей, основанных на дифференциальных уравнениях. Их ключевые особенности:

1. Линейность: состояние обновляется линейно (s(t) = A·s(t-1) + B·x(t)), без нелинейных активаций.

2. Дискретизация: параметры выводятся из непрерывных уравнений для работы с дискретными токенами.

3. Сжатое состояние: вся история последовательности сжимается в вектор фиксированного размера.

Отличия от других моделей

Ядро архитектуры:

ds(t)/dt = A·s(t) + B·x(t)
y(t) = C·s(t) + D·x(t)

Где:

• x(t) — входной сигнал (токен) в момент времени t

• s(t) — скрытое состояние (память ^[6] модели)

• ds(t)/dt — скорость изменения состояния

• A — матрица переходов (определяет “забывание” прошлого)

• B — матрица входа (влияние нового токена на состояние)

• C — матрица выхода (преобразует состояние в выход)

• D — сквозная связь (прямое влияние входа на выход)

• y(t) — выходной сигнал

Дискретизация для токенов:

A_d = exp(-Δt * A)   # Дискретная матрица переходов
B_d = (A⁻¹)(exp(Δt·A) - I)B  # Дискретная матрица входа
s_t = A_d · s_{t-1} + B_d · x_t

Где:

• A_d — дискретный аналог матрицы A (определяет “сохранение памяти”)

• B_d — дискретный аналог матрицы B (влияние входа на обновление состояния)

• Δt — шаг дискретизации (учится: большой = долгая память, маленький = быстрое забывание ^[7])

2. Селективность

Уникальность Mamba:

B = Linear(x_t)  # Линейное преобразование входа
Δt = softplus(Linear(x_t))  # Активация softplus: log(1 + exp(x))

Где:

• Linear() — полносвязный слой (y = Wx + b)

• softplus() — гладкая версия ReLU, гарантирует Δt > 0

Модель динамически решает:

• “Важный токен? Запомню надолго (↑ Δt)”

• “Шум? Проигнорирую (↓ Δt)”

3. Параллельный Scan

Решение проблемы RNN:

state = cumprod(A) * cumsum(B)  # O(log n) вместо O(n)

Где:

• cumprod() — кумулятивное произведение (a1, a1a2, a1a2*a3, …)

• cumsum() — кумулятивная сумма (b1, b1+b2, b1+b2+b3, …)

Как работает:

1. Разбиваем последовательность на блоки

2. Вычисляем промежуточные состояния внутри блоков параллельно

3. Объединяем результаты между блоками

4. Повторяем ^[8] иерархически (дерево слияний)

---

Разберём на простом примере

Обработка фразы “Мама мыла раму”

1. Токенизация

"М"→10, "а"→11, " "→12, "м"→13, "ы"→14, "л"→15, "р"→16, "у"→17
Последовательность: [10, 11, 13, 11, 12, ...]

2. Эмбеддинг

Каждый токен → вектор:

10 → [0.2, -0.1, 0.4, 1.1]
11 → [0.7, 0.3, -0.2, 0.5]

3. Блок Mamba

Для токена “м” (позиция 2):

1. Локальный контекст (Conv1D):

   conv("Ма") = [0.5, 0.1, 0.3, 0.9]  # Смешение соседей
   

2. Селективное обновление состояния:

   Δt = sigmoid("м") → 0.7  # Высокая важность
   new_state = (1 - 0.7*A) * state + 0.7*B * x_token
   

3. Gating механизм:

   gate = sigmoid(Linear(x))  # Решает, какую информацию передать
   output = gate * (C * state + D * x_token)
   

4. Выход: y = output

4. Предсказание

После 12 блоков:

logits = linear_layer(output)  # Вероятности символов
next_token = argmax(logits) → "а"  # "Мама..."

---

Код: Сердце Mamba

Ядро SSM

class MambaBlock(nn.Module):
    def forward(self, x):
        # Локальный контекст
        x_conv = depthwise_conv1d(x)
        
        # Селективные параметры
        Δ, B, C = self.x_proj(x_conv)  
        A_d = exp(-Δ * self.A)
        
        # Параллельный scan
        state = cumprod(A_d) * cumsum(B * x_conv)
        y = einsum('btd,btd->bt', state, C) + self.D * x_conv
        
        # Gating механизм
        return y * torch.sigmoid(self.gate_proj(x))

Параллельный Scan

def parallel_scan(A, B):
    A_cum = torch.cumprod(A, dim=1)  # Продукт: [a0, a0*a1, a0*a1*a2, ...]
    B_cum = torch.cumsum(B * A_cum, dim=1)  # Взвешенная сумма
    return B_cum / (A_cum + 1e-7)  # Нормализация

---

Сравнение: Mamba vs Трансформер

Сильные стороны Mamba:

1. Анализ ДНК/белковых последовательностей.

2. Работа на edge-устройствах (телефоны).

Слабые стороны:

1. Короткие тексты (трансформеры эффективнее).

2. Мультимодальные задачи (пока).

---

Примеры применения

1. 🧬 BioMamba:

   • Анализ генома человека (3 млрд пар оснований).

2. 🖼️ Vim (Vision Mamba):

   • На 30% быстрее ViT на ImageNet.

   • Статья ^[9].

Резюме

Mamba — прорыв для длинных последовательностей:

• State Space Model с селективностью.

• Сложность O(n) vs O(n²) у трансформеров.

• Применения: геномика, длинные тексты, edge-устройства.

• Ограничения: мультимодальность, короткие контексты.

Ссылки:

1. Оригинальная статья ^[10]

2. Объяснение SSM ^[11]

---

Философский итог

Mamba не заменяет трансформеры, а расширяет инструментарий ИИ:

• Для длинных данных — оптимальный выбор.

• Для мультимодальности — трансформеры сохраняют преимущество. Будущее: Гибридные архитектуры, где Mamba обрабатывает историю, а внимание — кросс-модальные связи.

---

Проверь себя

1. Почему сложность Mamba O(n), а не O(n²)?

2. Как селективность помогает анализировать ДНК?