LIME for ECG Time Series Dataset Example

LIME (Local Interpretable Model-Agnostic Explanations) — популярный модет в решении задачи интерпретации. Он основан на простой идее — приблизить прогнозы сложного оценщика (например, нейронной сети) простым — обычно линейной/логистической регрессией.

Применить LIME можно из коробки при помощи одноименной библиотеки [lime ^[1]](https://github.com/marcotcr/lime ^[1]). Однако, при применении LIME к, в частности, к временным рядам возникают особенности:

• При интерпретации нужно учесть, что временные ряды — это структурированные последовательности.

• Интерпретация проводится не по отдельным признакам, а по сегментам времени: насколько важен отрезок сигнала с 20-й по 30-ю миллисекунду?

• Для генерации соседних примеров нужно аккуратно вносить изменения в части сигнала, соответствующие сегментам: заменой на шум, среднее значение или другие методы.

поэтому в чистом виде lime для TimeSeries не всегда легко применить. И в этом туториале мы сделаем приближенение метода самостоятельно! :)

А именно, вы:

• Узнаете, как использовать LIME для интерпретации моделей классификации сигналов ЭКГ;

• Разберете способ генерации осмысленных локальных возмущений;

• Обучите локальную модель, имитирующую поведение ^[2] основной нейросети;

• Визуализируете, какие сегменты ЭКГ сигнала оказались наиболее значимыми для классификации.

Работать будем с PyTorch + Scikit-learn. Весь код, как всегда, будет на гитхаб.

Step 0. Loading and Preprocessing the Dataset

Работать будем с набором данных про ЭКГ. А именно, в нашем распряжении будут записи ЭКГ по четырем классам:

1. Нормальный синусовый ритм;

2. Мерцательная аритмия;

3. Желудочковая тахикардия;

4. Сердечный приступ.

Более подробная информация про датасет [здесь ^[3]].

# Path to the dataset
file_path_train = 'https://github.com/SadSabrina/XAI-open_materials/blob/main/LIME_for_Time_Series/data/ecg_train.csv?raw=True'
file_path_test = 'https://github.com/SadSabrina/XAI-open_materials/blob/main/LIME_for_Time_Series/data/ecg_test.csv?raw=True'

# Training dataset
ecg_train = pd.read_csv(file_path_train, header=None)
# Testing dataset
ecg_test = pd.read_csv(file_path_test, header=None)

Сделаем несколько шагов классической предобработки — посмотрим на пропуски, бесконечности и уберем их. Затем, поделим данные на X и y, подберем метрику и приступим к подготовке модели. Все эти шаги описаны в ноутбуке, на них подробно останавливаться не будем.

Step 1. Building a CNN Model

Дальше, оформим модель, на основе которой будем решать задачу. На самом деле, в силу данных, можно было бы обойтись интерпретируемой моделью. Но так как цель туториала — практика в интерпретации черных ящиков — решим задачу при помощи сверточной сети.

class ECGCNN(nn.Module):
    def __init__(self, input_shape, num_classes):
        """
        input_shape: tuple time_steps, channels (exmaple 140, 1)
        num_classes: number of output classes
        """
        super(ECGCNN, self).__init__()
        time_steps, channels = input_shape

        self.conv1 = nn.Conv1d(in_channels=channels, out_channels=64, kernel_size=3)
        self.pool = nn.MaxPool1d(kernel_size=2)
        self.dropout = nn.Dropout(0.5)

        # Compute output length after conv and pooling
        conv_output_length = time_steps - 2  # kernel_size=3 reduces by 2
        pool_output_length = conv_output_length // 2  # MaxPool1d(pool_size=2)

        self.flattened_size = 64 * pool_output_length
        self.fc1 = nn.Linear(self.flattened_size, 100)
        self.fc2 = nn.Linear(100, num_classes)

    def forward(self, x):
        """
        x: Tensor of shape (batch_size, time_steps, channels)
        """
        if type(x) != torch.Tensor:
          x = torch.Tensor(x)

        x = x.permute(0, 2, 1)  # Change to (batch_size, channels, time_steps)
        x = F.relu(self.conv1(x))
        x = self.pool(x)
        x = self.dropout(x)
        x = x.contiguous().view(x.size(0), -1)  # Flatten
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return torch.log_softmax(x, dim=1)  # Use CrossEntropyLoss, so no softmax here (pyTorch CrossEntropyLoss expects unbounded scores)

    def forward_probs(self, x):

      x = self.forward(x)
      return torch.exp(x)

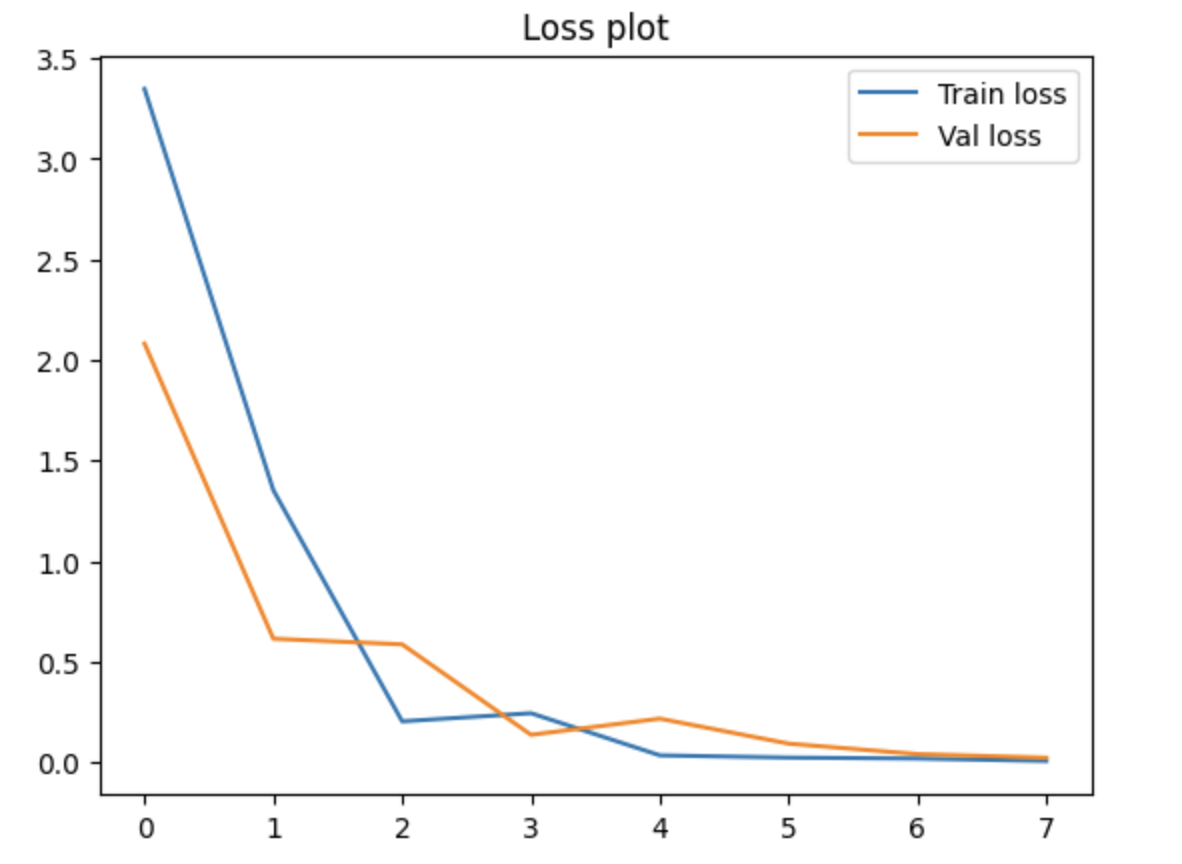
Обучение ^[4] даст нам такой график, так что теперь приступим к LIME!

Step 2. LIME for Time Seris Domain

По определению, объяснение LIME — это локальная интерпретируемая модель, которая аппроксимирует поведение ^[5] исходной сложной модели в окрестности конкретного объекта $x in mathbb{R}^d$ ($d$ — количество признаков в объекте).

Математически ^[6] это задача оптимизации:

где:

• — сложная (исходная) модель, например нейросеть;

• — интерпретируемая модель (обычно линейная), G красивая здесь — это множество всех интепретируемых моделей;

• — вес, отражающий близость объекта к ; обычно вычисляется как:

  , где D — расстояние (например, косинусное), — ширина ядра;

• — локальная функция потерь, измеряющая насколько хорошо приближает в окрестности — мы будем брать MSE;

• — мера сложности интерпретируемой модели (например, число ненулевых коэффициентов).

На практике, чтобы использовать эту формулу, нам нужны:

1. Конкретное наблюдение – его будем объяснять;

2. То, что мы будем считать за признаки во временном ряду (в нашем случае семгенты временного ряда);

3. Окрестность — множество наблюдений вокруг ;

4. Прогнозы — на вариантах из полученной окресности;

5. Обученная интерпретируемая модель на точках из окресности (обученная с учётом весов ), веса которой и будут отражать важность;

Соберем всё по шагам.

Шаг 1. Конкретное наблюдение

Здесь можно взять любой индекс и забрать его из датасета. У нас будет 11й.

idx_ecg = 11                         # сhoose interested index from rows
instance_ecg = ecg_test_x.iloc[idx_ecg, :].values     # extract the selected instance from the test dataset

plt.figure(figsize=(16, 5))
plt.plot(instance_ecg)
plt.title('ECG instance to explain');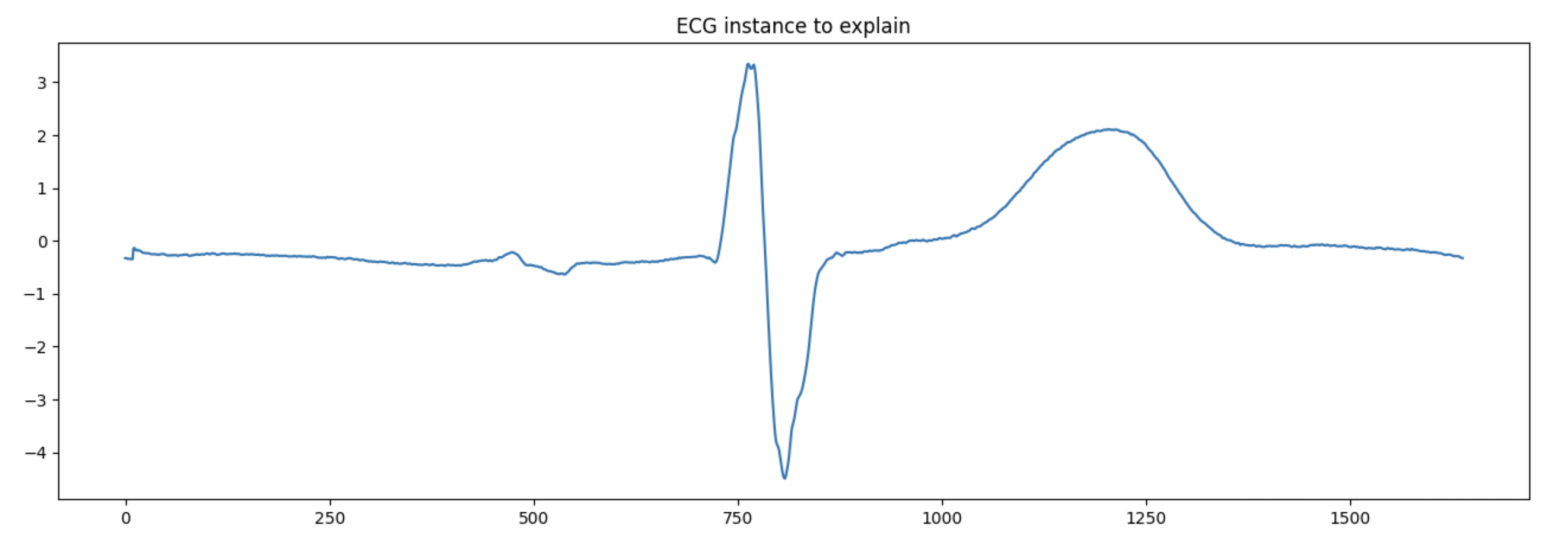

Получим для него вероятности и класс.

# Predict the class of the selected signal by trained model
probability_vector = model.forward_probs(torch.Tensor(np.expand_dims(instance_ecg.reshape(1, -1), axis=2)))

print("Probability vector of the selected instance:", probability_vector)

# Probability vector of the selected instance: tensor([[3.3614e-06, 8.0830e-01, 1.9169e-01, 1.8729e-06]],
      # grad_fn=<ExpBackward0>)
  
# class labels
class_labels = [0, 1, 2, 3]

predicted_class = torch.argmax(probability_vector).item()

print("Available classes:", class_labels)
print("Predicted Class for the selected instance:", predicted_class)

# Available classes: [0, 1, 2, 3]
# Predicted Class for the selected instance: 1

Шаг 2. Получение сегментов-признаков.

Методом “пристального взгляда” подберем количество сегментов. Более правильный и формальный способ — подбирать количество сегментов в зависимости от природы сигнала.

Сегменты получим простым образом — нарезкой ряда на равные кусочки. А именно, для ряда с временными шагами мы делим его на отрезков фиксированной длины:

где — длина одного сегмента.

Дальше мы строим индексы границ отрезков следующим образом:

Где последний сегмент может включать “хвост”:

Это нужно, чтобы даже если длина ряда не делится на нацело, последний сегмент корректно включит все оставшиеся точки.

L = len(instance_ecg) # TS length
K = 13 # number of slices

l = L // K # slice width

# Segment start points
segment_edges = [i * l for i in range(K)] + [L]
# Segment centers 
segment_centers = [(segment_edges[i] + segment_edges[i+1]) // 2 for i in range(K)]
# Segment labels
segment_labels = [f'{i+1}' for i in range(K)]

# Plot segmented instance
plt.figure(figsize=(12, 3))
plt.plot(instance_ecg, label='Original signal')

for i in range(1, K):
  plt.axvline(x=i*l, color='r', linestyle='--')

plt.xticks(ticks=segment_centers, labels=segment_labels, fontsize=9)
plt.title('Segmented the instance ECG signal')
plt.xlabel('Segment index')
plt.ylabel('Signal Amplitude')
plt.legend()
plt.show()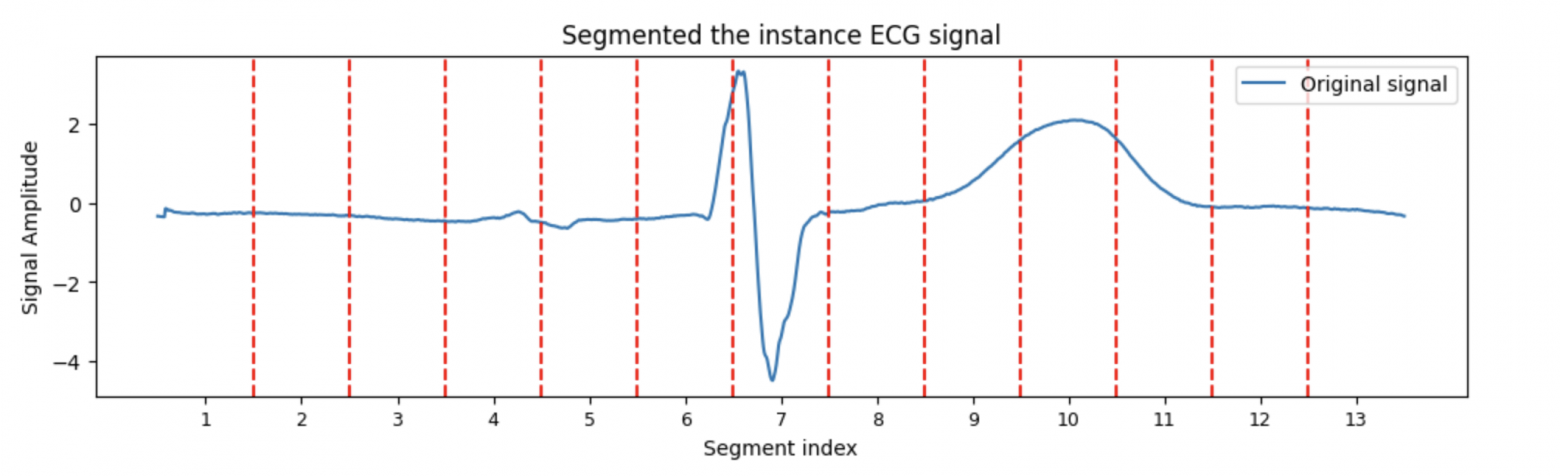

Шаг 3. Генерация наблюдений в окресности.

Будем генерировать наблюдения из окресности следующим образом. Для изначального наблюдения будем выбирать случайные номера сегментов , и вносить в них изменения по одной из трех стратегий:

• “mean” — меняем значения сегмента на среднее по сегменту;

• “noise” — меняем значения сегмента на значения из нормального распределения, со средним и стандартным отклонением по сегменту;

• “zero” — просто обнуляем значения сегмента

Все замены будем проводить по кусочкам .

# Segment slices function
def split_series(series, num_slices):

    length = series.shape[0]
    slice_len = int(np.ceil(length / num_slices))
    return [(i * slice_len, min((i + 1) * slice_len, length)) for i in range(num_slices)]

slices = split_series(instance_ecg, 13)


def generate_perturbations(series, slices, num_samples, replacement="mean", pertub_power=0.2):
    perturbed = []
    masks = []
    for _ in range(num_samples):
        mask = np.ones(len(slices), dtype=int)
        idx_to_perub = np.random.choice(len(slices), size=int(len(slices)*pertub_power), replace=False) # менять за раз будем pertub_power% от всех кусочков
        mask[idx_to_perub] = 0

        copy = series.copy()
        for i in idx_to_perub:
            start, end = slices[i]
            if replacement == "mean":
                copy[start:end] = np.mean(series[start:end])
            elif replacement == "zero":
                copy[start:end] = 0
            elif replacement == "noise":
                copy[start:end] = np.random.normal(series[start:end].mean(), series[start:end].std(), end - start) #.reshape(1, -1)
        perturbed.append(copy)
        masks.append(mask)

    return np.array(perturbed), np.array(masks)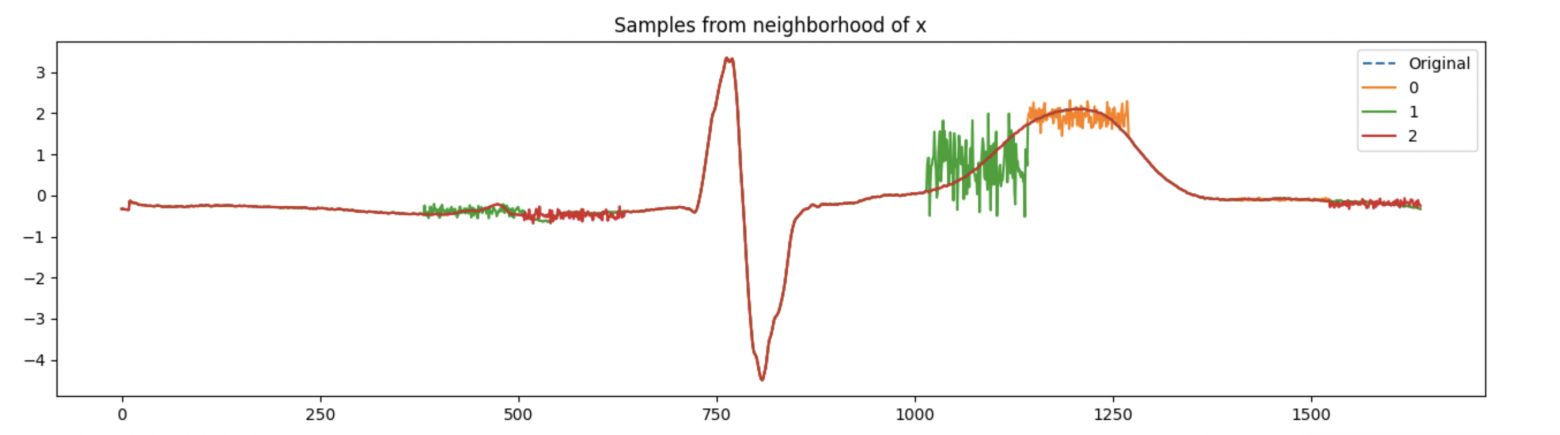

Обратите внимание ^[7], на этом шаге мы получими маски (masks). Для обучения интерпретируемой модели набор данных будет представлен бинарными признаками для каждого сегмента. Признак равен 1, если соответствующий сегмент включен, и 0, если он был искажен. Такой подход используется также при реализации LIME для [текстовых данных ^[8]].

Шаг 4. Обучение интерпретируемой модели в окресности.

Чтобы обучить модель будем, вместо решения исходной задачи, решать задачу обеспечения похожести интерпретируемой модели на модель-черный ящик. Для этого будем обучать модель давать прогнозы такие же, какими их дает исходная модель.

Обучать модель будем на вероятностях и в соответствие с важностью наблюдения. А именно, чем ближе он к исходному объекту, тем весомее он должен быть при обучении.

# Probabilities for all observations from the neighborhood

probs = np.exp(model(np.expand_dims(pertub, axis=2)).detach().numpy())

# Calculate the distances

distances = cosine_distances(pertub, instance_ecg.reshape(1, -1)).ravel()

def train_lime_ridge(perturbations, predictions, distances, target_class, alpha=1.0, kernel_width=0.25):
    """
    Train interpretable model (Ridge)

    Parameters:
        perturbations (np.array): features [N x K], mask
        predictions (np.array): матрица [N x C], вероятности классов
        distances (np.array): длина N, расстояния до оригинала
        target_class (int): индекс класса, который объясняется
        alpha (float): коэффициент регуляризации Ridge
        kernel_width (float): ширина ядра для весов

    Returns:
        (weights, intercept, score): коэф. модели, свободный член, R^2 на подмножестве
    """
    # LIME exponential kernel
    weights = np.exp(- (distances ** 2) / (kernel_width ** 2))

    # target
    y = predictions[:, target_class]

    # simple Ridge-regression train
    model = Ridge(alpha=alpha)
    model.fit(perturbations, y, sample_weight=weights)

    return model.coef_, model.intercept_, model.score(perturbations, y, sample_weight=weights)

w, b, score = train_lime_ridge(masks, probs, distances, 0, alpha=.8)

B теперь, когда у нас есть модель, мы можем использовать её веса для интерпретации основной модели по сегментам. Сделаем это в виде двух графиков. Код для отрисовки приложен в ноутбуке.

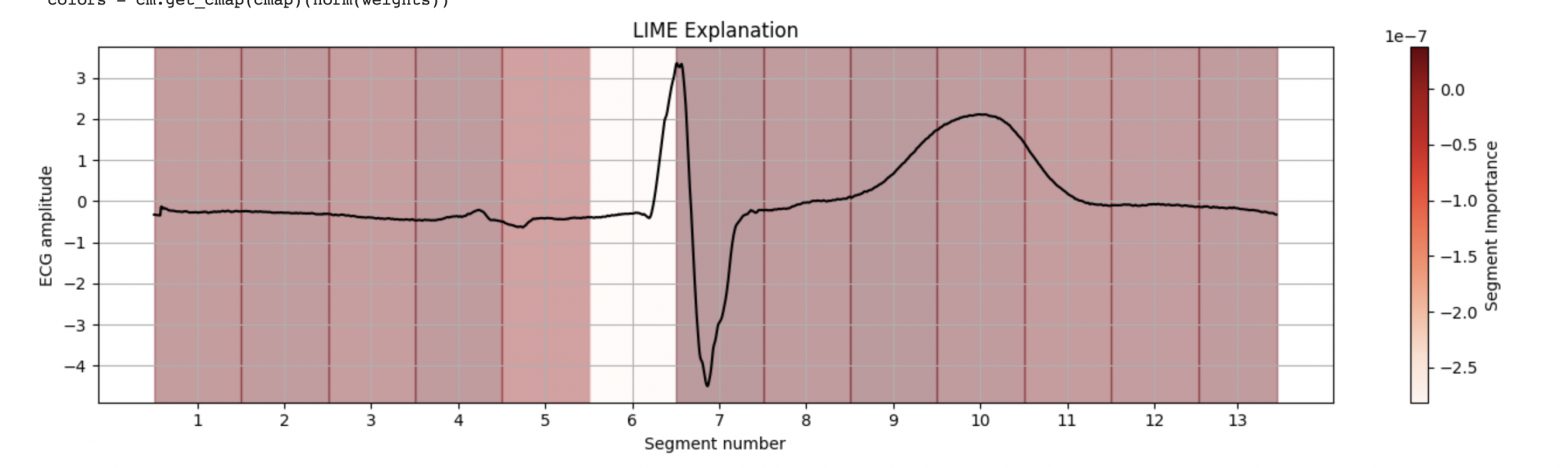
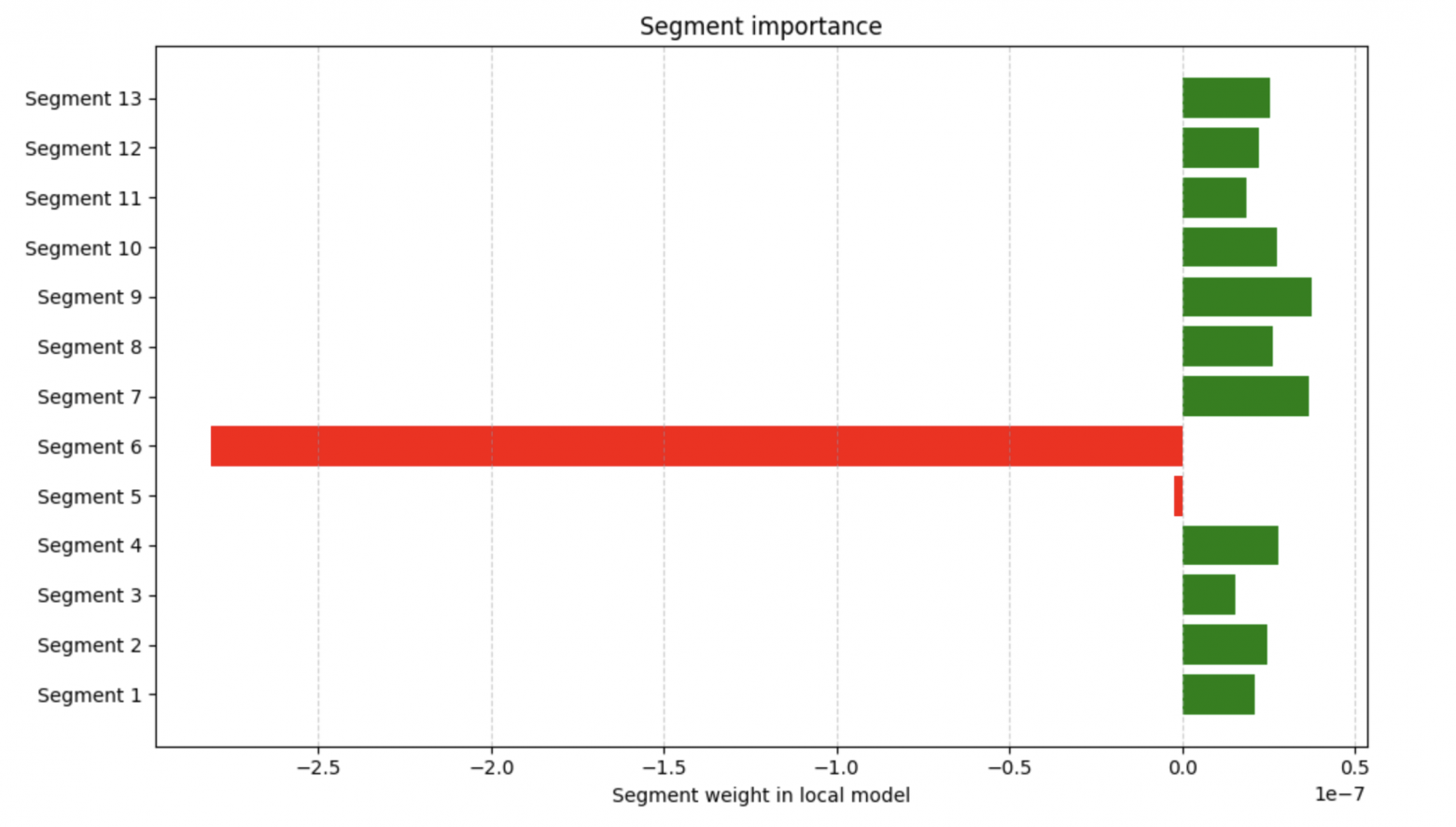
Готово! Спасибо, друзья!

В этом туториале мы рассмотрели применение метода LIME к задаче интерпретации модели классификации временных рядов на примере ЭКГ-сигналов. Для этого:

• обучили простую сверточную нейросеть для распознавания классов ЭКГ;

• реализовали механизм генерации локальных объяснений с помощью сегментации временного ряда;

• построили визуализации важности сегментов как поверх сигнала, так и в виде диаграммы весов.

LIME позволил нам локально аппроксимировать поведение модели и оценить, какие части сигнала оказали наибольшее влияние на её предсказание.

Несмотря на простоту реализации, LIME остаётся мощным и гибким инструментом для анализа моделей с любыми типами входных данных. Однако стоит помнить, что качество интерпретации зависит от выбора параметров (например, числа сегментов) и стратегии генерации “окрестности” (можете поиграть также с параметрами функций и оценить насколько пошатнутся веса).

Основные материалы туториала:

[1](https://github.com/mdhabibi/LIME-for-Time-Series/tree/main?tab=readme-ov-file ^[9])
[2](https://github.com/emanuel-metzenthin/Lime-For-Time/tree/master ^[10])
[3](https://arxiv.org/abs/1602.04938 ^[11]).

Новые туториалы:

За ними всегда жду вас в [дата-блоге ^[12]]!
Обещаю публиковать материалы чаще! :)

Со всем самым добрым,

Ваш Дата-автор!