Ученые научились быстрее находить положение минимума функции, не вычисляя ее значений

Российские ученые из МФТИ, Сколтеха и Иннополиса провели теоретическое исследование и компьютерное моделирование новых методов оптимизации, основанных на использовании сравнений значений функции между собой без знания самих значений этой функции и ее производных. Им удалось построить более эффективные алгоритмы, чем традиционные, и открыть обсуждение использования концепции порядковых оракулов в вычислении. Работа опубликована ^[1] в материалах конференции NeurIPS 2024.

Проблема черного ящика (black-box problem) в задачах оптимизации относится к ситуации, когда целевая функция или система, которую нужно оптимизировать, является непрозрачной и недоступной для анализа. Одним из подходов в решении подобных проблем являются порядковые оракулы, которые позволяют сравнивать значения функции, не обращаясь к ее значениям непосредственно, что может облегчить решение задачи оптимизации. 

С недавним появлением концепции порядковых оракулов исследователи начали изменять подходы к оптимизации, используя информацию о порядке значений функции для создания более совершенных алгоритмов. Эта концепция становится особенно важной в контексте многих современных приложений, таких как обучение ^[2] с подкреплением ^[3], кросс-валидация и оптимизация гиперпараметров, где доступ к данным часто ограничен.

В свежей статье, представленная на конференции NeurIPS 2024, авторы предлагают новые подходы. Они создали оптимизационный алгоритм, который использует порядковый оракул, и предложили способ ускорения этого алгоритма. Исследователи подтвердили теоретическую состоятельность предложенных методов через численные эксперименты, которые продемонстрировали их высокую производительность. 

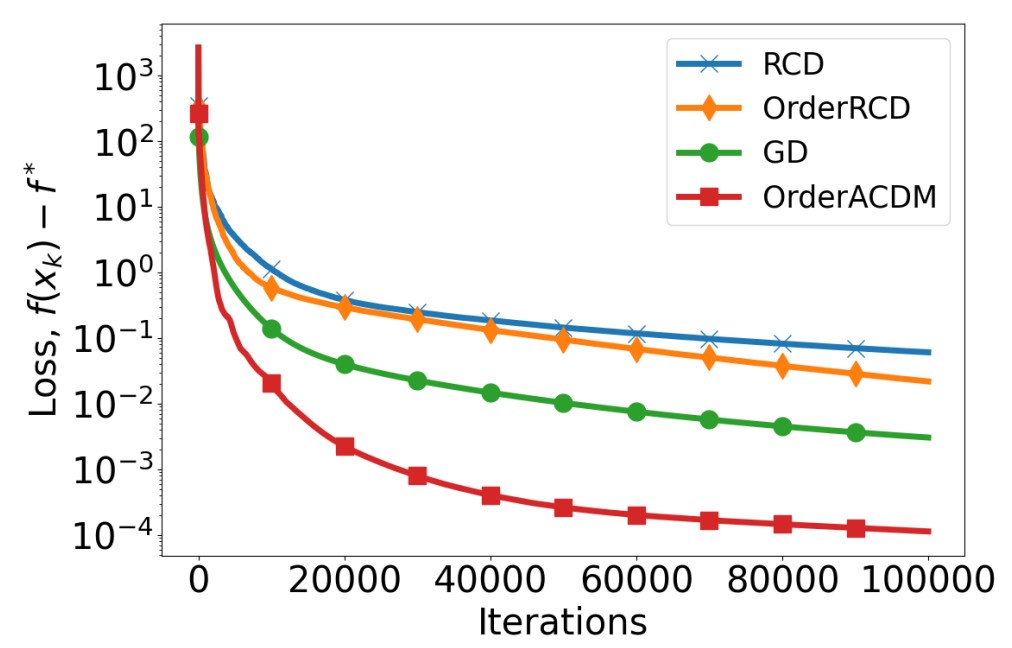
Математики ^[4] сравнили, как быстро работают два алгоритма с оракулом порядка: случайный спуск по координатам с оракулом порядка (OrderRCD) и ускоренный спуск по координатам с оракулом порядка (OrderACDM). Они также сравнили их с традиционными неускоренными алгоритмами, такими как случайный спуск по координатам RCD (алгоритм Нестерова) и градиентный спуск GD.

Неускоренные алгоритмы как RCD, так и OrderRCD показали более низкую скорость сходимости по сравнению с градиентным спуском, что подтверждило теоретические выводы российских ученых. Оказалось, что OrderRCD даже превосходит аналогичный метод первого порядка RCD, несмотря на ограничения в использовании оракула. Это связано с тем, что OrderRCD на каждой итерации использует точный шаг в направлении наискорейшего спуска, находя его с помощью метода золотого сечения GRM. Кроме того, оказалось, что ускоренный метод OrderACDM достигает большей скорости сходимости, чем все неускоренные алгоритмы, включая RCD и GD.

Математики отдельно рассмотрели три случая различных видов функций: невыпуклые, выпуклые и сильно выпуклые. Оказалось, что в случае сильно выпуклых функций алгоритм показал линейную сходимость, что позволяет значительно уменьшить количество итераций, необходимых для достижения точности. Кроме того, исследователи рассмотрели случай стохастической оптимизации и показали возможные перспективы для разработки новых стохастических алгоритмов.

«Работа по внедрению концепции порядкового оракула в практику оптимизации — это важный шаг к решению сложных задач, стоящих перед современной наукой ^[5] о данных и машинным обучением, — рассказал Александр Гасников, заведующий лабораторией математических методов оптимизации МФТИ. — Научное сообщество благодаря этой концепции располагает мощным инструментом, способным обеспечить значительное улучшение в скорости и эффективности оптимизационных процессов». 

Работа по внедрению концепции порядкового оракула в практику оптимизации — это важный шаг к решению сложных задач, стоящих перед современной наукой о данных и машинным обучением. Научное сообщество благодаря этой концепции располагают мощным инструментом, способным обеспечить значительное улучшение в скорости и эффективности оптимизационных процессов.

Авторы не только предложили новые эффективные алгоритмы, но и открыли обсуждения для будущих исследований, связывая их с реальными задачами, такими как ухудшение пользовательского опыта ^[6] в реактивных системах или настройки в распределенных обучающих средах. Кроме того, в своей работе они предложили практические рекомендации по использованию разработанных ими алгоритмов.