HIGGS: Новый алгоритм квантования нейросетей

С развитием LLM, более актуальной становится проблема сокращения вычислительных затрат. Одним из самых эффективных решений является квантование – представление параметров модели в низкой точности (например, 4 бита вместо 32). Однако существующие методы квантования страдают от отсутствия строгого теоретического обоснования и оптимальности. HIGGS – новый подход, который решает эти проблемы, основываясь на доказанной авторами теореме линейности.
Статья на arXiv ^[1]
HuggingFace ^[2]

Что такое квантование и почему оно важно?

Квантование – один из наиболее эффективных способов уменьшения размера и вычислительных затрат больших моделей (таких как Llama и Qwen). Базовый подход предполагает разбиение задачи на отдельные послойные задачи:

• Каждый слой модели представлен весовой матрицей

• Квантование слоя сводится к выбору квантованных весов , минимизирующих некоторую ошибку ^[3] (обычно MSE ^[4]).

Подробнее про квантизацию можно посмотреть здесь ^[5](очень подробное объяснение с картинками)

Однако до сих пор оставался неясным вопрос, как послойная ошибка влияет на общую точность модели (например, perplexity). На практике разные слои по-разному влияют на общую ошибку модели, и текущие методы не учитывают это различие в значимости слоев.

Что такое perplexity?

Метрика perplexity отражает, насколько хорошо модель предсказывает выборку текста. Чем меньше значение perplexity, тем лучше модель справляется с предсказанием. Perplexity вычисляется по формуле:

где:

• — это последовательность слов (или токенов) в тестовой выборке;

• — вероятность того, что модель предскажет слово , зная предыдущие слова;

• — количество слов в тестовой выборке.

Perplexity связана с понятием кросс-энтропии ^[6] и энтропии информации ^[7]. Кросс-энтропия характеризует разницу между двумя распределениями вероятностей: истинным распределением данных и распределением, предсказанным моделью. Perplexity является экспонентой от кросс-энтропии, выраженной в битах. Таким образом, чем меньше perplexity, тем ближе распределение, предсказанное моделью, к истинному распределению данных, и тем меньше энтропия, возникающая при генерации следующего слова.

Теорема линейности

Авторы статьи формулируют и доказывают ключевую теорему линейности, связывающую ошибки квантования отдельных слоёв с ростом общей perplexity модели. Теорема утверждает следующее:

При условии, что ошибки квантования относительно малы, среднее значение perplexity квантованной модели может быть аппроксимировано формулой:

где:

• – исходные веса предобученной модели.

• – квантованные веса.

• – коэффициенты, зависящие только от исходных весов слоя l.

• – относительная ошибка квантования слоя:

Почему это важно?

Эта теорема впервые чётко показывает, что глобальная ошибка (perplexity) линейно зависит от послойных ошибок квантования. Это открывает два новых направления:

1. Оптимальное послойное квантование: минимизация perplexity сводится к минимизации ошибок MSE послойно.

2. Динамическое квантование: выбор разной битности квантования для каждого слоя с учётом его значимости.

Метод HIGGS

Основываясь на теореме линейности, строится новый метод квантования HIGGS (Hadamard Incoherence with Gaussian MSE-optimal GridS), состоящий из двух шагов:

• Предварительное преобразование (Random Hadamard Transform, RHT):

Весовая матрица умножается на случайную матрицу Адамара ^[8] , в результате чего распределение весов становится близким к гауссовскому:

• Квантование с MSE-оптимальной сеткой:

Весам присваиваются значения ближайшей точки из заранее вычисленной оптимальной сетки, минимизирующей среднеквадратичную ошибку для нормального распределения:

Такое сочетание даёт минимальную ошибку квантования и, благодаря теореме линейности, минимальное увеличение общей perplexity.

Оптимальное распределение битности

Теорема линейности позволяет сформулировать задачу динамического распределения битности следующим образом:

Нужно выбрать битность для каждого слоя так, чтобы минимизировать рост perplexity при заданной средней разрядности . Формально это записывается как задача оптимизации:

где – размер слоя, – суммарное число параметров.

Эта задача решается методами динамического программирования, что позволяет найти оптимальное решение за считанные секунды даже для огромных моделей.

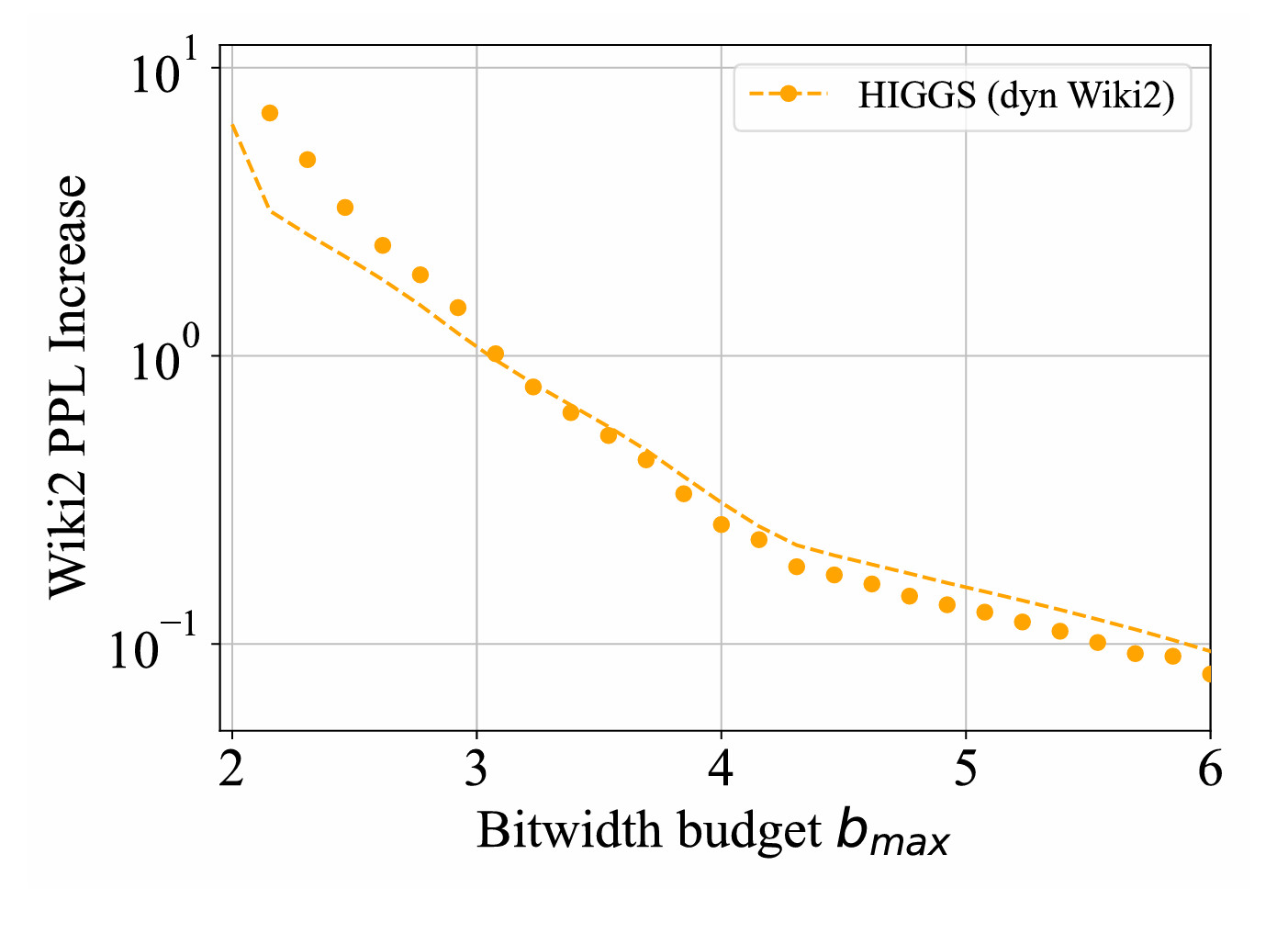
Результаты экспериментов

Авторы проверили HIGGS и динамическое квантование на моделях Llama 3 и Qwen:

• Метод HIGGS стабильно показывает меньшую perplexity, чем популярные подходы NF (Normal Float) и AF ^[10](Abnormal Float), особенно в 3-4 бита.

• Динамическое квантование даёт дополнительный прирост качества.

• Использование FLUTE ^[11]GPU-ядер показало ускорение в 2–3 раза по сравнению с FP16, почти без потери точности.

Итог

Таким образом HIGGS решает старые проблемы квантования моделей, основываясь не на эмпирических наблюдениях, а на строгой математически ^[12] доказанной теореме линейности.

Если вам интересны такого рода посты, можете подписаться на мой канал в telegram ^[13], там я пишу посты поменьше. В основном я затрагиваю темы применения математики (от базовой до нейросетей) в видеоиграх, но также уделяю внимание ^[14] видеоиграм как области искусства. Но и про разборы статей не забываю.