Привет, друзья!

В этой серии статей мы разбираем структуры данных и алгоритмы, представленные в этом замечательном репозитории ^[1]. Это одиннадцатая часть серии.

Сегодня мы рассмотрим несколько простых, но интересных алгоритмов машинного обучения ^[2], а также один весьма любопытный статистический алгоритм.

Код, представленный в этой и других статьях серии, можно найти в этом репозитории ^[3].

Интересно? Тогда прошу под кат.

• Первая часть ^[4]
• Вторая часть ^[5]
• Третья часть ^[6]
• Четвертая часть ^[7]
• Пятая часть ^[8]
• Шестая часть ^[9]
• Седьмая часть ^[10]
• Восьмая часть ^[10]
• Девятая часть ^[10]
• Десятая часть ^[10]

❯ Машинное обучение

❯ NanoNeuron

NanoNeuron (далее — нейрончик) — это очень упрощенная версия концепции нейронов из нейронных сетей. Нейрончик умеет конвертировать значения температуры из градусов Цельсия в градусы Фаренгейта.

Код примера содержит 7 простых функций (затрагивающих предсказание модели, вычисление стоимости, прямое/обратное распространение и обучение), позволяющих понять, как машины на самом деле “обучаются”. В коде нет сторонних библиотек, внешних зависимостей или наборов данных, только чистые и простые функции.

Эти функции не являются руководством по машинному обучению. Многие концепции машинного обучения отсутствуют и упрощены! Упрощение преследует цель дать читателю самое базовое понимание того, как учатся машины, а также того, что машинное обучение — это не магия, а математика ^[11].

Чему NanoNeuron будет учиться?

Вероятно, вы слышали о нейронах в контексте нейронных сетей ^[12]. Нейрончик — это как раз такой нейрон ^[13], только проще. Мы реализуем его с нуля. Для простоты мы даже не будем создавать сеть из нейрончиков. Он будет работать сам по себе, делая некоторые “магические” предсказания для нас. Мы научим его конвертировать (предсказывать) температуру в градусах Фаренгейта на основе температуры в градусах Цельсия.

Кстати, формула для такого преобразования следующая:

f = c * 1.8 + 32

Но пока наш нейрончик о ней не знает.

Модель NanoNeuron

Определим функцию моделирования нейрончика. Она реализует базовую линейную зависимость между x и y, которая выглядит как y = w * x + b. Проще говоря, наш нейрончик — это “ребенок” в “школе”, который учится рисовать прямую линию в системе координат XY.

Переменные w и b — это параметры модели. Нейрончику известны только эти параметры линейной функции. Он “выучит” значения этих параметров в процессе обучения.

Единственная вещь, которую умеет делать нейрончик, — это имитация линейной зависимости. В методе predict() он принимает некоторый x и предсказывает y. Никакой магии:

function NanoNeuron(w, b) {
  this.w = w;
  this.b = b;
  this.predict = (x) => {
    return x * this.w + this.b;
  }
}

Линейная регрессия ^[14] — это ты?🧐

Преобразование градусов

function celsiusToFahrenheit(c) {
  const w = 1.8;
  const b = 32;
  const f = c * w + b;
  return f;
};

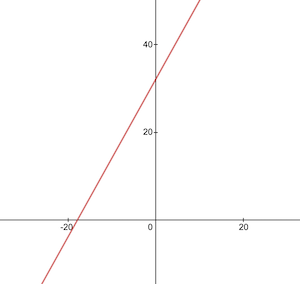
Мы хотим научить нейрончика имитировать эту функцию, т.е. научить, что w = 1.8, а b = 32 без предоставления этих значений.

Графически эту функцию можно представить следующим образом:

Генерация наборов данных

Перед обучением модели нужно сгенерировать наборы тренировочных и тестовых данных на основе функции celsiusToFahrenheit(). Наборы состоят из пар входных значений и правильно размеченных результатов.

В реальной жизни данные, как правило, собираются, а не генерируются. Например, у нас может быть набор изображений с рукописными цифрами и набор соответствующих цифр.

Для обучения нейрончика используется тренировочный набор. Перед тем, как нейрончик вырастет и сможет принимать решения самостоятельно, мы должны объяснить ему, что такое хорошо и что такое плохо с помощью тренировочных примеров.

Тестовый набор используется для проверки того, насколько хорошо нейрончик обрабатывает данные, которых он не видел в процессе обучения. Это та точка, когда мы видим, что наш “ребенок” вырос и может принимать самостоятельные решения:

function generateDataSets() {
  // xTrain -> [0, 1, 2, ...],
  // yTrain -> [32, 33.8, 35.6, ...]
  const xTrain = [];
  const yTrain = [];
  for (let x = 0; x < 100; x += 1) {
    const y = celsiusToFahrenheit(x);
    xTrain.push(x);
    yTrain.push(y);
  }

  // xTest -> [0.5, 1.5, 2.5, ...]
  // yTest -> [32.9, 34.7, 36.5, ...]
  const xTest = [];
  const yTest = [];
  // Начиная с 0.5 и используя такой же шаг 1,
  // который мы использовали для тренировочного набора,
  // мы обеспечиваем уникальность данных
  for (let x = 0.5; x < 100; x += 1) {
    const y = celsiusToFahrenheit(x);
    xTest.push(x);
    yTest.push(y);
  }

  return [xTrain, yTrain, xTest, yTest];
}

Стоимость (ошибка ^[15]) предсказания

Нам нужен какой-то критерий верности предсказания. Вычисление стоимости (ошибки) между правильным значением y и prediction (предсказанием), сделанным нейрончиком, производится по следующей формуле:

predictionCost = (y - prediction) ** 2 * 0.5

Это просто разница между двумя значениями. Чем ближе значения друг к другу, тем меньше разница. Мы используем степень 2 для избавления от отрицательных чисел, поэтому (1 - 2) ** 2 = (2 - 1) ** 2. Деление на 2 выполняется для упрощения дальнейшей формулы обратного распространения (см. ниже):

function predictionCost(y, prediction) {
  return (y - prediction) ** 2 / 2;
}

Прямое распространение

Прямое распространение (forward propagation) означает выполнение предсказаний для всех тренировочных примеров из наборов xTrain и yTrain и вычисление средней стоимости этих предсказаний.

Мы позволяет нейрончику играть в “угадайку”. Он может сильно ошибаться. Средняя стоимость покажет нам, насколько некорректной является наша модель. Эта стоимость очень важна, поскольку влияет на параметры w и b, которыми оперирует нейрончик. Повторное выполнение прямого распространения показывает, стал ли нейрончик умнее после соответствующих изменений.

Средняя стоимость вычисляется по такой формуле:

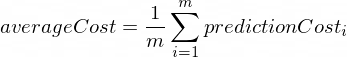
Где m — это количество тренировочных примеров (100 в нашем случае).

function forwardPropagation(model, xTrain, yTrain) {
  const m = xTrain.length;
  const predictions = [];
  let cost = 0;
  for (let i = 0; i < m; i += 1) {
    const prediction = nanoNeuron.predict(xTrain[i]);
    cost += predictionCost(yTrain[i], prediction);
    predictions.push(prediction);
  }
  // Нас интересует средняя стоимость
  cost /= m;
  return [predictions, cost];
}

Обратное распространение

После того, как мы узнали, насколько верными являются предсказания модели (на основе средней стоимости), как нам сделать их более точными?

Ответ — обратное распространение (backward propagation). Обратное распространение — это процесс оценки стоимости предсказания и модификации параметров w и b таким образом, чтобы будущие предсказания были более точными.

В этом месте машинное обучение выглядит как магия. Ключевой концепцией здесь является производная (derivative), которая показывает, какой шаг необходимо предпринять, чтобы подобраться к минимальной функции стоимости (minimum cost function).

Помните, что нахождение минимальной функции стоимости — это конечная цель обучения. Если мы нашли значения w и b, которые делают среднюю стоимость маленькой, значит, модель будет делать хорошие и точные предсказания.

Производные — это большая и отдельная тема, выходящая за рамки нашей беседы. MathIsFun ^[16] — отличный ресурс для начала погружения в эту тему.

Производная, по сути, является касательной к кривой функции, которая указывает в направлении минимума функции:

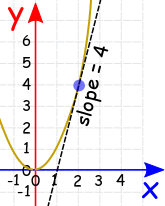
Из приведенного графика следует, что если мы находимся в точке (x=2, y=4), то кривая “говорит” нам двигаться влево и вниз для достижения минимума функции.

Производные функции averageCost() для параметров w и b выглядят так:

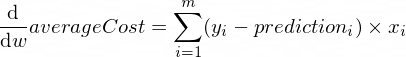
Где m — количество тренировочных примеров (100 в нашем случае).

function backwardPropagation(predictions, xTrain, yTrain) {
  const m = xTrain.length;
  // В начале мы не знаем, как менять параметры 'w' и 'b'.
  // Поэтому устанавливаем шаг изменения для каждого параметра в 0
  let dW = 0;
  let dB = 0;
  for (let i = 0; i < m; i += 1) {
    dW += (yTrain[i] - predictions[i]) * xTrain[i];
    dB += yTrain[i] - predictions[i];
  }
  // Нас интересует средняя дельта каждого параметра
  dW /= m;
  dB /= m;
  return [dW, dB];
}

Обучение модели

Теперь мы знаем, как оценивать корректность модели для всех тренировочных примеров (прямое распространение). Мы также знаем, как применять небольшие модификации параметров w и b модели (обратное распространение). Но проблема состоит в том, что однократного запуска прямого и обратного распространений недостаточно для того, чтобы наша модель извлекла какие-то уроки из тренировочных данных. Это можно сравнить с одним днем обучения ребенка в школе. Ребенок ходит в школу не однажды, а день за днем и год за годом, чтобы чему-нибудь научиться.

Поэтому распространения следует повторять ^[17] много раз. Это как раз то, что делает функция trainModel(). Это как учитель для нашего нейрончика:

• он проводит некоторое время (epochs) с нашим глупым нейрончиком и пытается его чему-то научить
• он использует специальные “книги” (наборы данных xTrain и yTrain) для обучения
• он заставляет нейрончика учиться усерднее (быстрее) с помощью параметра оценки обучения alpha

Несколько слов об alpha. Это просто произведение dW и dB, вычисленных в процессе обратного распространения. Производная указывает нам направление, в котором мы должны двигаться для достижения минимума функции стоимости (положительные/отрицательные знаки dW и dB), а также скорость, с которой мы должны двигаться в этом направлении (абсолютные значения dW и dB). Нам нужно умножить эти шаги на alpha, чтобы ускорить или замедлить наше движение к минимуму. При использовании больших значений для alpha можно просто перепрыгнуть минимум и никогда его не найти.

Если использовать аналогию с учителем, то можно сказать, что чем сильнее учитель будет давить на ребенка, тем быстрее он будет учиться, но если учитель будет давить слишком сильно, то у ребенка случится нервный срыв и больше учиться он не сможет 🤯

Параметры w и b будут обновляться следующим образом:

w = w + alpha * dW
b = b + alpha * dB

Функция обучения:

function trainModel({model, epochs, alpha, xTrain, yTrain}) {
  // История обучения
  const costHistory = [];

  // Перебираем эпохи
  for (let epoch = 0; epoch < epochs; epoch += 1) {
    // Прямое распространение
    const [predictions, cost] = forwardPropagation(model, xTrain, yTrain);
    costHistory.push(cost);

    // Обратное распространение
    const [dW, dB] = backwardPropagation(predictions, xTrain, yTrain);

    // Модифицируем параметры модели для повышения точности предсказаний
    nanoNeuron.w += alpha * dW;
    nanoNeuron.b += alpha * dB;
  }

  return costHistory;
}

Вместе веселее

Применим созданные функции.

Создаем экземпляр NanoNeuron. В данный момент нейрончику неизвестны значения w и b. Устанавливаем их произвольно:

const w = Math.random(); // например -> 0.9492
const b = Math.random(); // например -> 0.4570
const nanoNeuron = new NanoNeuron(w, b);

Генерируем наборы данных:

const [xTrain, yTrain, xTest, yTest] = generateDataSets();

Обучаем модель небольшими шагами (0.0005) на протяжении 7000 эпох. Эти значения были определены эмпирическим путем, не стесняйтесь их менять:

const epochs = 70000;
const alpha = 0.0005;
const trainingCostHistory = trainModel({ model: nanoNeuron, epochs, alpha, xTrain, yTrain });

Проверяем функцию стоимости в процессе обучения. Мы ожидаем, что стоимость после обучения будет значительно ниже, чем до него. Это будет означать, что нейрончик стал умнее. Противоположное также возможно:

console.log('Стоимость до обучения:', trainingCostHistory[0]); // например, 4694.3335043
console.log('Стоимость после обучения:', trainingCostHistory[epochs - 1]); // например, 0.0000024

Графически снижение стоимости выглядит так (ось x — количество эпох):

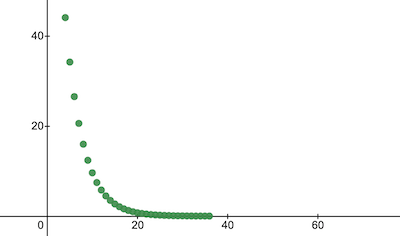
Взглянем на параметры модели. Мы ожидаем, что w и b нейрончика будут близки к истинным (w = 1.8 и b = 32):

console.log('Параметры нейрончика:', { w: nanoNeuron.w, b: nanoNeuron.b }); // например -> { w: 1.8, b: 31.99 }

Оцениваем точность модели на тестовых данных, чтобы увидеть, как хорошо нейрончик справляется с обработкой неизвестных данных. Мы ожидаем, что стоимость тестовых предсказаний будет близка к стоимости тренировочных предсказаний:

[testPredictions, testCost] = forwardPropagation(nanoNeuron, xTest, yTest);
console.log('Стоимость тестовых предсказаний:', testCost); // например -> 0.0000023

Теперь, поскольку наш “ребенок” хорошо показал себя при обучении в “школе” и научился правильно обрабатывать данные, которых он не видел, мы можем назвать его “умным” и задать ему парочку вопросов. В этом и заключалась цель обучения:

const tempInCelsius = 70;
const customPrediction = nanoNeuron.predict(tempInCelsius);
console.log(`Нейрончик "думает", что ${tempInCelsius}°C в градусах Фаренгейта:`, customPrediction); // -> 158.0002
console.log('Правильный ответ:', celsiusToFahrenheit(tempInCelsius)); // -> 158

Очень близко! Наш нейрончик хорош, но не идеален, как все люди :)

// Модель NanoNeuron (нейрончика).
// Она реализует базовую линейную зависимость между 'x' и 'y': y = w * x + b.
// Проще говоря, наш нейрончик - это "ребенок", умеющий рисовать прямую линию в системе координат XY.
// w, b - параметры модели
class NanoNeuron {
  constructor(w, b) {
    // Нейрончику известны только эти два параметра линейной функции.
    // Значения этих параметров будут определяться нейрончиком в процессе обучения
    this.w = w
    this.b = b
  }
  // Все, что умеет нейрончик, - имитировать линейную зависимость.
  // Он принимает некоторый 'x' и предсказывает 'y'. Никакой магии
  predict(x) {
    return x * this.w + this.b
  }
}

// Конвертирует градусы Цельсия в градусы Фаренгейта по формуле: f = 1.8 * c + 32.
// Мы хотим научить нейрончика имитировать эту функцию, т.е.
// научить, что W = 1.8, а B = 32 без предоставления этих значений.
// c - температура в градусах Цельсия
// f - вычисленная температура в градусах Фаренгейта
const W = 1.8
const B = 32
function celsiusToFahrenheit(c) {
  const f = c * W + B
  return f
}

// Генерирует обучающий и тестовый наборы данных с помощью функции celsiusToFahrenheit().
// Наборы состоят из пар входных значений и правильно размеченных результатов.
// В реальной жизни в большинстве случаев эти данные будут собраны, а не сгенерированы.
// Например, у нас может быть набор изображений рукописных цифр и
// набор соответствующих цифр
function generateDataSets() {
  // Генерируем ТРЕНИРОВОЧНЫЕ данные.
  // Эти данные будут использоваться для обучения модели.
  // Перед тем, как нейрончик вырастет и сможет принимать решения самостоятельно,
  // мы должны объяснить ему, что такое хорошо и что такое плохо с помощью
  // тренировочных примеров.
  // xTrain -> [0, 1, 2, ...],
  // yTrain -> [32, 33.8, 35.6, ...]
  const xTrain = []
  const yTrain = []
  for (let x = 0; x < 100; x += 1) {
    const y = celsiusToFahrenheit(x)
    xTrain.push(x)
    yTrain.push(y)
  }

  // Генерируем ТЕСТОВЫЕ данные.
  // Эти данные будут использоваться для оценки того, насколько хорошо модель работает с данными,
  // которых она не видела в процессе обучения. Здесь мы можем увидеть,
  // что наш "ребенок" вырос и может принимать решения самостоятельно.
  // xTest -> [0.5, 1.5, 2.5, ...]
  // yTest -> [32.9, 34.7, 36.5, ...]
  const xTest = []
  const yTest = []
  // Начиная с 0.5 и используя такой же шаг 1,
  // который мы использовали для тренировочного набора,
  // мы обеспечиваем уникальность данных
  for (let x = 0.5; x < 100; x += 1) {
    const y = celsiusToFahrenheit(x)
    xTest.push(x)
    yTest.push(y)
  }

  return [xTrain, yTrain, xTest, yTest]
}

// Вычисляем стоимость (ошибку) между правильным значением 'y' и
// 'prediction' (предсказанием), сделанным нейрончиком
function predictionCost(y, prediction) {
  // Это просто разница между двумя значениями.
  // Чем ближе значения друг к другу, тем меньше разница.
  // Мы используем здесь степень 2 только для того, чтобы избавиться от отрицательных чисел,
  // поэтому (1 - 2) ^ 2 = (2 - 1) ^ 2.
  // Результат делится на 2 просто для упрощения дальнейшей формулы обратного распространения (см. ниже)
  return (y - prediction) ** 2 / 2 // например -> 235.6
}

// Прямое распространение.
// Эта функция берет все примеры из тренировочных наборов xTrain и yTrain
// и вычисляет предсказания модели для каждого примера из xTrain.
// По пути она также вычисляет среднюю стоимость предсказаний
function forwardPropagation(model, xTrain, yTrain) {
  const m = xTrain.length
  const predictions = []
  let cost = 0
  for (let i = 0; i < m; i += 1) {
    const prediction = model.predict(xTrain[i])
    cost += predictionCost(yTrain[i], prediction)
    predictions.push(prediction)
  }
  // Нас интересует средняя стоимость
  cost /= m
  return [predictions, cost]
}

// Обратное распространение.
// В этом месте машинное обучение выглядит как магия.
// Ключевой концепцией здесь является производная (derivative), которая показывает, какой шаг нужно предпринять, чтобы
// приблизиться к минимуму функции стоимости. Помните, нахождение минимальной функции стоимости -
// конечная цель процесса обучения. Функция стоимости выглядит следующим образом:
// (y - prediction) ^ 2 * 1/2, где prediction = x * w + b.
function backwardPropagation(predictions, xTrain, yTrain) {
  const m = xTrain.length
  // В начале мы не знаем, как менять параметры 'w' и 'b'.
  // Поэтому устанавливаем шаг изменения для каждого параметра в значение 0
  let dW = 0
  let dB = 0
  for (let i = 0; i < m; i += 1) {
    // Это производная функции стоимости параметра 'w'.
    // Она показывает, в каком направлении (положительный/отрицательный знак 'dW') и
    // на сколько (абсолютное значение 'dW') параметр 'w' должен быть изменен
    dW += (yTrain[i] - predictions[i]) * xTrain[i]
    // Это производная функции стоимости параметра 'b'.
    // Она показывает, в каком направлении (знак 'dB') и
    // на сколько (абсолютное значение 'dB') параметр 'b' должен быть изменен
    dB += yTrain[i] - predictions[i]
  }
  // Нас интересуют средняя дельта каждого параметра
  dW /= m
  dB /= m
  return [dW, dB]
}

// Обучает модель.
// Это "учитель" нашего нейрончика:
// - он проводит некоторое время (epochs) с нашим глупым нейрончиком и пытается его чему-то научить,
// - он использует специальные "книги" (наборы данных xTrain и yTrain) для обучения,
// - он заставляет ребенка учиться усерднее (быстрее) с помощью параметра оценки обучения 'alpha'
// (чем сильнее стимул, тем быстрее модель учится, но если учитель будет давить слишком сильно
// у "ребенка" может случиться нервный срыв, и больше он не сможет учиться)
function trainModel(model, epochs, alpha, xTrain, yTrain) {
  // История обучения модели.
  // Она может содержать хорошие или плохие "оценки" (стоимость),
  // полученные в процессе обучения
  const costHistory = []

  // Перебираем эпохи
  for (let i = 0; i < epochs; i += 1) {
    // Прямое распространение для всех тренировочных примеров.
    // Сохраняем стоимость текущей итерации.
    // Это поможет анализировать обучение модели
    const [predictions, cost] = forwardPropagation(model, xTrain, yTrain)
    costHistory.push(cost)

    // Обратное распространение. Учимся на ошибках.
    // Эта функция возвращает небольшие модификации, которые нужно применить к параметрам 'w' и 'b',
    // чтобы сделать предсказания более точными
    const [dW, dB] = backwardPropagation(predictions, xTrain, yTrain)

    // Модифицируем параметры нейрончика для повышения точности его предсказаний
    nanoNeuron.w += alpha * dW
    nanoNeuron.b += alpha * dB
  }

  // Возвращаем историю обучения для анализа и визуализации
  return costHistory
}

// ===
// Создаем экземпляр модели.
// В данный момент нейрончику неизвестны значения параметров 'w' и 'b'.
// Устанавливаем их произвольно
const w = Math.random() // например -> 0.9492
const b = Math.random() // например -> 0.4570
const nanoNeuron = new NanoNeuron(w, b)

// Генерируем тренировочные и тестовые наборы данных
const [xTrain, yTrain, xTest, yTest] = generateDataSets()

// Обучаем модель небольшими шагами (0.0005) в течение 70000 эпох.
// Можете попробовать другие значения, они определены эмпирическим путем
const epochs = 70000
const alpha = 0.0005
const trainingCostHistory = trainModel(
  nanoNeuron,
  epochs,
  alpha,
  xTrain,
  yTrain,
)

// Проверим, как менялась стоимость в процессе обучения.
// Мы ожидаем, что стоимость после обучения будет значительно ниже, чем до него.
// Это будет означать, что наш нейрончик стал умнее. Но возможно и обратное
console.log('Стоимость до обучения:', trainingCostHistory[0]) // например -> 4694.3335043
console.log('Стоимость после обучения:', trainingCostHistory[epochs - 1]) // например -> 0.0000024

// Взглянем на параметры нейрончика, чтобы увидеть, чему он научился.
// Мы ожидаем, что значения параметров 'w' и 'b' модели будут близки к истинным значениям,
// которые используются в функции celsiusToFahrenheit() (w = 1.8 и b = 32)
console.log(
  'Параметры нейрончика:',
  JSON.stringify({ w: nanoNeuron.w, b: nanoNeuron.b }, null, 2),
) // например -> { w: 1.8, b: 31.99 }

// Оцениваем точность модели на тестовых данных, чтобы увидеть, насколько хорошо она обрабатывает неизвестные данные.
// Мы ожидаем, что стоимость тестовых предсказаний будет близкой к стоимости тренировочных предсказаний.
// Это будет означать, что нейрончик хорошо справляется как с тренировочными, так и с тестовыми данными
const [testPredictions, testCost] = forwardPropagation(nanoNeuron, xTest, yTest)
console.log('Стоимость тестовых предсказаний:', testCost) // например -> 0.0000023

// После того, как "ребенок" хорошо показал себя в "школе" в процессе обучения и хорошо справился с тестовыми данными,
// мы можем назвать его "умным" и задать ему парочку вопросов
const tempInCelsius = 70
const customPrediction = nanoNeuron.predict(tempInCelsius)
console.log(
  `Нейрончик "думает", что ${tempInCelsius}°C в градусах Фаренгейта:`,
  customPrediction,
) // -> 158.0002
console.log('Правильный ответ:', celsiusToFahrenheit(tempInCelsius)) // -> 158
// Очень близко! Нейрончик хорош, но не идеален, как все люди :)

Пропущенные концепции машинного обучения

Следующие концепции машинного обучения были пропущены или упрощены.

Разделение данных

Обычно, у нас имеется один большой набор данных. Часто он разделяется в пропорции 70/30 для тренировочного/тестового набора (это зависит от количества примеров). Данные должны произвольно перемешиваться перед разделением. Если примеров много (например, миллионы), то пропорция может быть ближе к 90/10 или даже к 95/5.

Сеть

Как правило, нейроны ^[18] не используются по отдельности. Настоящая сила заключается в нейронных сетях. Сеть можно научить гораздо более сложным вещам. Наш нейрончик больше похож на линейную регрессию, чем на нейронную сеть.

Нормализация

Перед обучением входные данные лучше нормализовать ^[19].

Векторная реализация

Для сетей векторные (матричные) вычисления работают намного быстрее, чем циклы for.

Минимум функции стоимости

Используемая нами функция стоимости очень упрощена. Она должна содержать логарифмические компоненты ^[20]. Обратите внимание ^[21], что изменение функции стоимости повлечет изменение ее производных, поэтому в обратном распространении также надо будет использовать другие формулы.

Функция активации

Обычно, результат нейрона пропускается через функцию активации, такую как сигмоида ^[22], ReLU ^[23] или аналоги.

❯ Метод k ближайших соседей

Описание

• Википедия ^[24]
• GeekForGeeks ^[25]
• Habr (код на Python) ^[26]
• YouTube ^[27]

Метод k ближайших соседей (k-nearest neighbors algorithm, k-NN) — метрический алгоритм для автоматической классификации объектов или регрессии. Он относится к методам машинного обучения с учителем (supervised).

В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны. В случае использования метода для регрессии, объекту присваивается среднее значение по k ближайшим к нему объектам, значения которых уже известны. Мы будем говорить в основном о классификации.

Алгоритм может быть применим к выборкам с большим количеством атрибутов (многомерным). Для этого перед применением нужно определить функцию расстояния; классический вариант такой функции — евклидова метрика ^[28].

Использование теоремы Пифагора для вычисления евклидова расстояния на плоскости

Принцип работы

• проверяется валидность данных и меток
• вычисляется евклидово расстояние между тестовым (целевым) и всеми обучающими образцами
• расстояния вместе с классами сортируются в возрастающем порядке
• выбирается k ближайших образцов (соседей), где число k задается заранее (как правило, выбирается нечетное число — 3, 5 и т.д.)
• итоговым прогнозом среди выбранных k ближайших соседей будет мода в случае классификации и среднее арифметическое в случае регрессии
• возвращается наиболее похожий класс (для классификации) или среднее значение (для регрессии)

Визуализация k-NN для лучшего понимания:

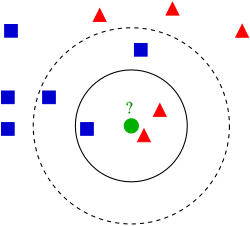
Пример классификации методом k-NN: тестовый образец (зеленый круг) должен быть классифицирован как синий квадрат (класс 1) или как красный треугольник (класс 2); если k=3, то он классифицируется как 2-й класс, потому что внутри меньшего круга 2 треугольника и только 1 квадрат; если k=5, то он будет классифицирован как 1-й класс (3 квадрата против 2 треугольников внутри большего круга)

Еще одна визуализация:

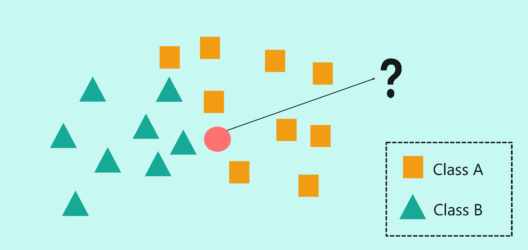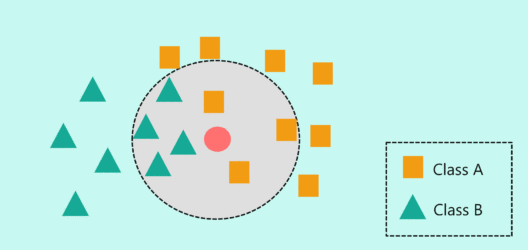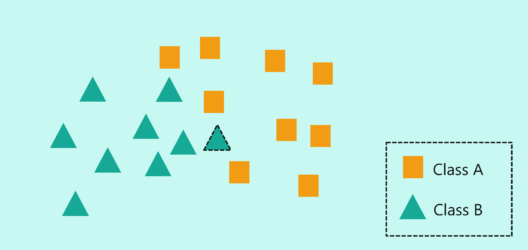
Здесь k = 7, поэтому тестовый образец классифицируется как зеленый треугольник

И еще одна:

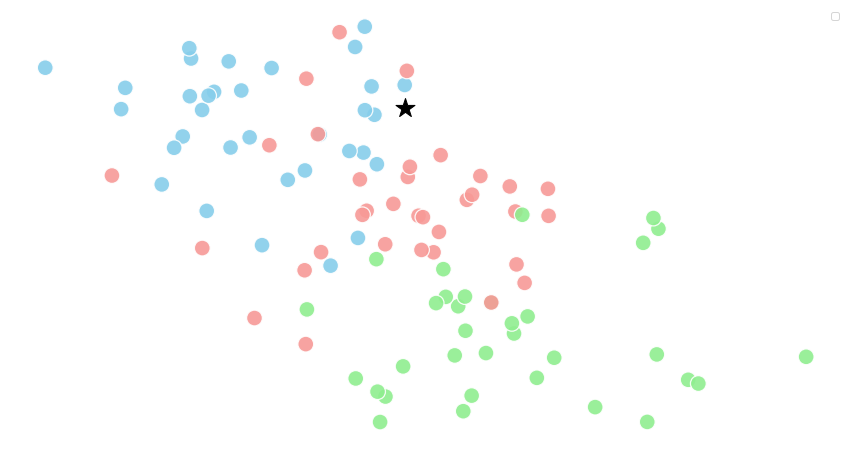
Звездочкой обозначен целевой образец

k=3

k=10

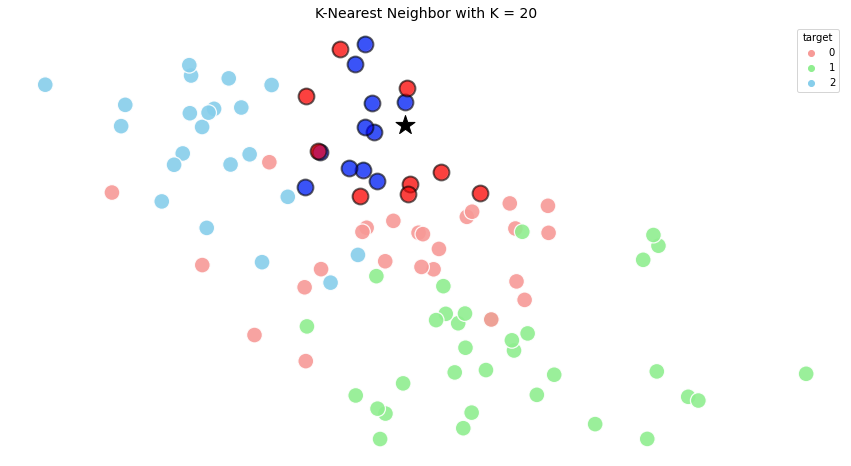
k=20

Как видим, во всех трех случаях целевой образец классифицируется как синий круг.

Реализация

// algorithms/machine-learning/k-nn.js
// Функция для вычисления евклидова расстояния
import euclideanDistance from '../math/euclidean-distance'

/** Функция принимает:
 * data   - данные
 * labels - метки
 * target - тестовый/целевой образец
 * k      - количество ближайших соседей
 */
export default function kNN(data, labels, target, k = 3) {
  if (!data || !labels || !target) {
    throw new Error('Отсутствует обязательный параметр')
  }

  // Вычисляем расстояние от `target` до каждой точки `data`.
  // Сохраняем расстояние и метку точки в списке
  const distances = []

  for (let i = 0; i < data.length; i++) {
    distances.push({
      distance: euclideanDistance([data[i]], [target]),
      label: labels[i],
    })
  }

  // Сортируем расстояния по возрастанию (от ближайшего к дальнему).
  // Берем `k` значений
  const kn = distances
    .sort((a, b) => {
      if (a.distance === b.distance) {
        return 0
      }
      return a.distance < b.distance ? -1 : 1
    })
    .slice(0, k)

  // Считаем количество экземпляров каждого класса
  const _labels = {}
  let topClass = 0
  let topClassCount = 0

  for (let i = 0; i < kn.length; i++) {
    if (kn[i].label in _labels) {
      _labels[kn[i].label] += 1
    } else {
      _labels[kn[i].label] = 1
    }

    if (_labels[kn[i].label] > topClassCount) {
      topClassCount = _labels[kn[i].label]
      topClass = kn[i].label
    }
  }

  // Возвращает класс с наибольшим количеством экземпляров
  return topClass
}

// algorithms/machine-learning/__tests__/k-nn.test.js
import kNN from '../k-nn'

describe('kNN', () => {
  it('при неправильных данных должно выбрасываться исключение', () => {
    expect(() => {
      kNN()
    }).toThrowError('Отсутствует обязательный параметр')
  })

  it('при неправильных метках должно выбрасываться исключение', () => {
    const noLabels = () => {
      kNN([[1, 1]])
    }
    expect(noLabels).toThrowError('Отсутствует обязательный параметр')
  })

  it('при отсутствии целевого образца должно выбрасываться исключение #1', () => {
    const noClassification = () => {
      kNN([[1, 1]], [1])
    }
    expect(noClassification).toThrowError('Отсутствует обязательный параметр')
  })

  it('при отсутствии целевого образца должно выбрасываться исключение #2', () => {
    const inconsistent = () => {
      kNN([[1, 1]], [1], [1])
    }
    expect(inconsistent).toThrowError('Матрицы имеют разную форму')
  })

  it('должен выполнить классификацию целевых образцов', () => {
    let dataSet
    let labels
    let toClassify
    let expectedClass

    dataSet = [
      [1, 1],
      [2, 2],
    ]
    labels = [1, 2]
    toClassify = [1, 1]
    expectedClass = 1
    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass)

    dataSet = [
      [1, 1],
      [6, 2],
      [3, 3],
      [4, 5],
      [9, 2],
      [2, 4],
      [8, 7],
    ]
    labels = [1, 2, 1, 2, 1, 2, 1]
    toClassify = [1.25, 1.25]
    expectedClass = 1
    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass)

    dataSet = [
      [1, 1],
      [6, 2],
      [3, 3],
      [4, 5],
      [9, 2],
      [2, 4],
      [8, 7],
    ]
    labels = [1, 2, 1, 2, 1, 2, 1]
    toClassify = [1.25, 1.25]
    expectedClass = 2
    expect(kNN(dataSet, labels, toClassify, 5)).toBe(expectedClass)
  })

  it('должен выполнить классификацию целевого образца с соседями на одинаковых расстояниях', () => {
    const dataSet = [
      [0, 0],
      [1, 1],
      [0, 2],
    ]
    const labels = [1, 3, 3]
    const toClassify = [0, 1]
    const expectedClass = 3
    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass)
  })

  it('должен выполнить классификацию целевого образца с соседями в трехмерном пространстве', () => {
    const dataSet = [
      [0, 0, 0],
      [0, 1, 1],
      [0, 0, 2],
    ]
    const labels = [1, 3, 3]
    const toClassify = [0, 0, 1]
    const expectedClass = 3
    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass)
  })
})

Запускаем тесты:

npm run test ./algorithms/machine-learning/__tests__/k-nn

❯ Метод k-средних

Описание

• Википедия ^[29]
• GeekForGeeks ^[30]
• Яндекс.Образование — Кластеризация ^[31]
• YouTube ^[32]

Метод k-средних (k-means) — наиболее популярный метод кластеризации. Он относится к методам машинного обучения без учителя (unsupervised).

Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров:

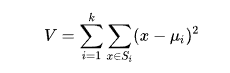
где k — число кластеров, Sⁱ — полученные кластеры, i = 1, 2, ..., k, а μⁱ — центры масс (центроиды) всех векторов x из кластера Sⁱ.

Принцип работы

Алгоритм разбивает множество элементов векторного пространства на заранее известное число кластеров k.

Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Для вычисления схожести между центром масс и векторами данных часто используется евклидова метрика ^[28].

Использование теоремы Пифагора для вычисления евклидова расстояния на плоскости

Алгоритм завершается, когда на какой-то итерации не происходит изменения внутрикластерного расстояния. Это происходит за конечное число итераций, так как количество возможных разбиений конечного множества конечно, а на каждом шаге суммарное квадратичное отклонение V уменьшается, поэтому зацикливание невозможно.

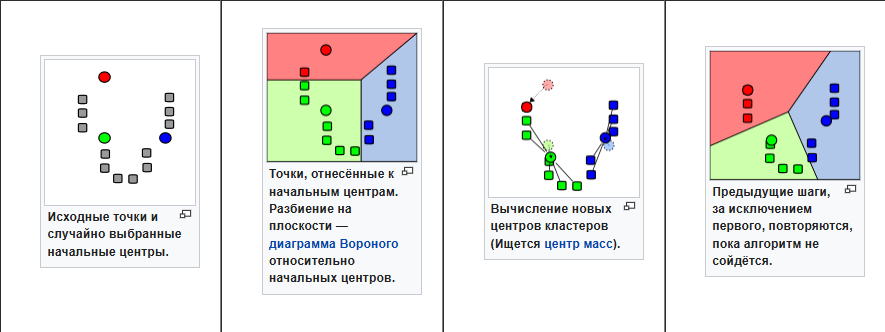
Действие алгоритма в двумерном случае. Начальные точки выбраны случайно

Последовательность шагов:

• проверяется валидность/согласованность данных
• инициализируется k центроидов с начальными/произвольными k точками
• вычисляется расстояние каждой точки до каждого центроида
• каждой точке присваивается значение метки ближайшего кластера
• вычисляется центроид каждого кластера на основе содержащихся в нем точек
• цикл повторяется до тех пор, пока положение центроидов не перестанет меняться

Визуализация для лучшего понимания:

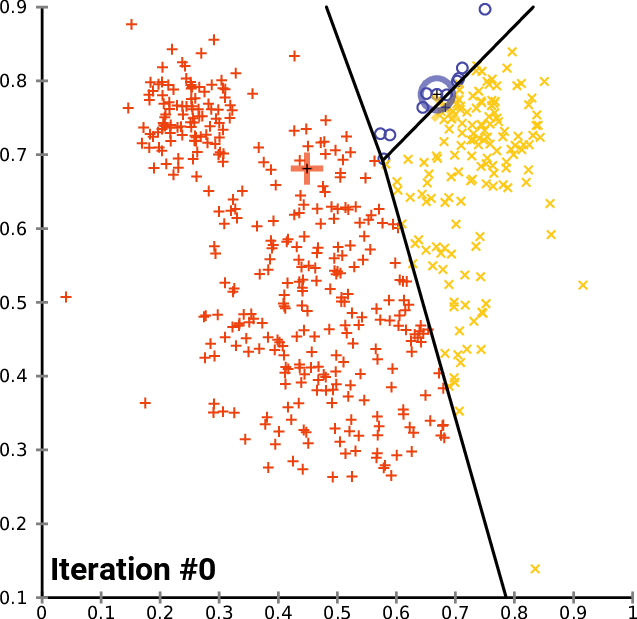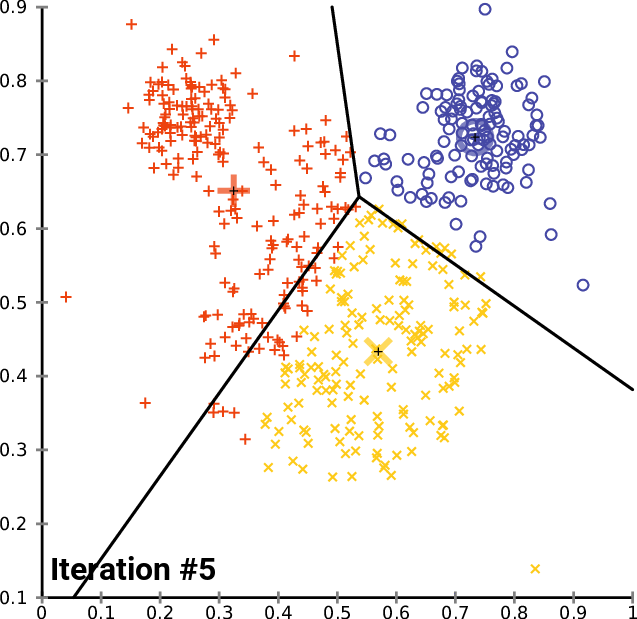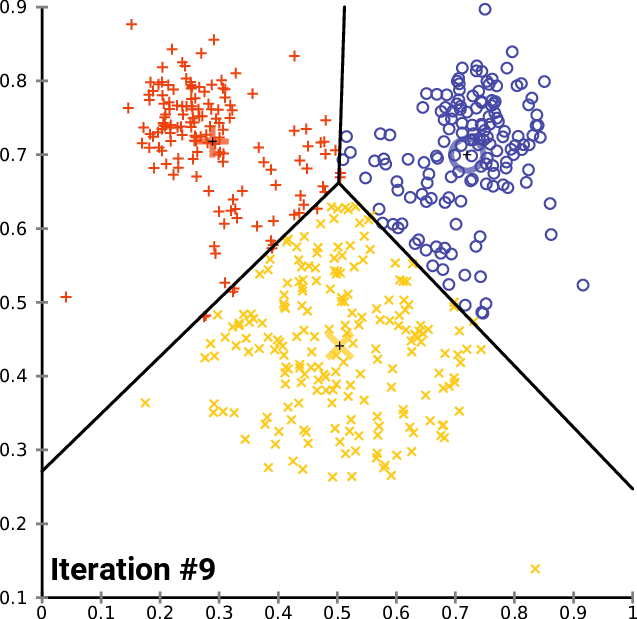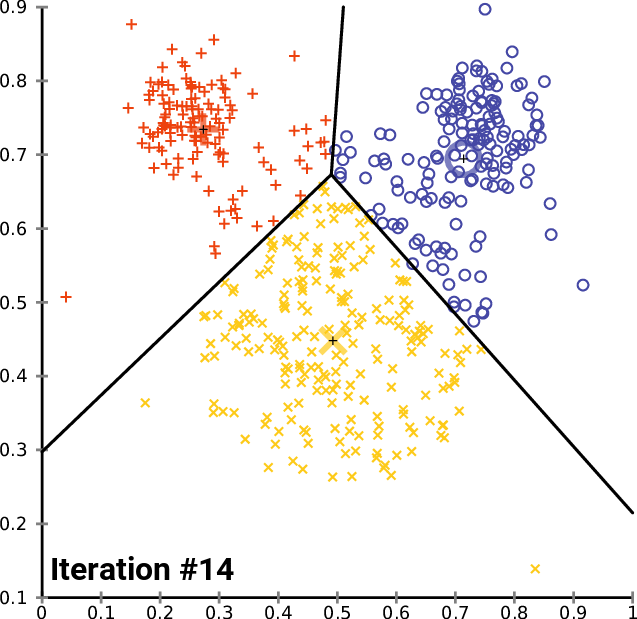
Проблемы k-средних

• не гарантируется достижение глобального минимума суммарного квадратичного отклонения V, а только одного из локальных минимумов

Типичный пример сходимости метода k-средних к локальному минимуму. В этом примере результат кластеризации указанным методом противоречит очевидной кластерной структуре множества данных. Маленькими кружками обозначены точки данных, четырехлучевые звезды — центроиды. Принадлежащие им точки данных окрашены в тот же цвет

• результат зависит от выбора исходных центров кластеров, их оптимальный выбор неизвестен

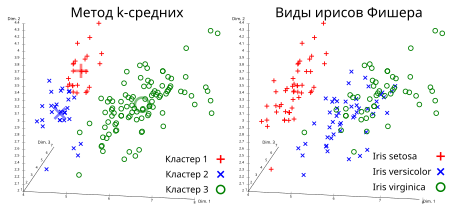
Результат кластеризации методом k-средних для ирисов Фишера и реальные виды ирисов, визуализированные с помощью ELKI. Центры кластеров отмечены с помощью крупных, полупрозрачных маркеров

• число кластеров надо знать заранее

Применение

В алгоритмах глубокого обучения метод k-средних иногда применяют не по прямому назначению (классификация разбивкой на кластеры), а для создания так называемых фильтров (ядер свертки, словарей). Например, для распознавания изображений в алгоритм k-средних подают небольшие случайные кусочки изображений обучающей выборки, допустим, размером 16х16 в виде линейного вектора, каждый элемент которого кодирует яркость своей точки. Количество кластеров k задается большим, например 256. Обученный метод k-средних при определенных условиях вырабатывает при этом центры кластеров (центроиды), которые представляют собой удобные базисы, на которые можно разложить любое входное изображение. Такие “обученные” центроиды в дальнейшем используют в качестве фильтров, например для сверточной нейронной сети в качестве ядер свертки или других аналогичных систем машинного зрения ^[33].

Реализация

// algorithms/machine-learning/k-means.js
// Утилиты для матричных вычислений
import * as matrix from '../math/matrix'
// Функция для вычисления евклидова расстояния
import euclideanDistance from '../math/euclidean-distance'

/** Функция принимает:
 * data - данные
 * k    - количество кластеров
 */
export default function kMeans(data, k = 1) {
  if (!data) {
    throw new Error('Отсутствуют данные для классификации')
  }

  // Количество измерений
  const dimension = data[0].length
  // Центроиды
  const centroids = data.slice(0, k)

  // Матрица расстояний от каждой точки до каждого центроида
  const distances = matrix.zeros([data.length, k])

  // Классы векторных точек данных.
  // - 1 означает, что класс еще не назначен
  const classes = new Array(data.length).fill(-1)

  // Индикатор итерации
  let iterate = true
  while (iterate) {
    iterate = false

    // Вычисляем и сохраняем расстояние каждой точки от каждого центроида
    for (let i = 0; i < data.length; i++) {
      for (let j = 0; j < k; j++) {
        distances[i][j] = euclideanDistance([centroids[j]], [data[i]])
      }

      // Присваиваем метку ближайшего кластера каждой точке
      const closestClusterIndex = distances[i].indexOf(
        Math.min(...distances[i]),
      )

      // Проверяем, был ли класс точки изменен
      // и нужно ли повторить итерацию
      if (classes[i] !== closestClusterIndex) {
        iterate = true
      }

      classes[i] = closestClusterIndex
    }

    // Пересчитываем положение центроида кластера
    // на основе содержащихся в нем точек
    for (let i = 0; i < k; i++) {
      // Сбрасываем координаты центроида, поскольку нам нужно их пересчитать
      centroids[i] = new Array(dimension).fill(0)
      let clusterSize = 0
      for (let j = 0; j < data.length; j++) {
        if (classes[j] === i) {
          // Регистрируем еще одну точку текущего кластера
          clusterSize += 1
          for (let l = 0; l < dimension; l++) {
            centroids[i][l] += data[j][l]
          }
        }
      }

      // Вычисляем среднее значение каждой координаты центроида
      for (let j = 0; j < dimension; j++) {
        centroids[i][j] = parseFloat(
          Number(centroids[i][j] / clusterSize).toFixed(2),
        )
      }
    }
  }

  return classes
}

// algorithms/machine-learning/__tests__/k-means.test.js
import KMeans from '../k-means'

describe('kMeans', () => {
  it('при невалидных данных должно выбрасываться исключение', () => {
    expect(() => {
      KMeans()
    }).toThrowError('Отсутствуют данные для классификации')
  })

  it('при несогласованных данных должно выбрасываться исключение', () => {
    expect(() => {
      KMeans([[1, 2], [1]], 2)
    }).toThrowError('Матрицы имеют разную форму')
  })

  it('должен выполнить кластеризацию', () => {
    const data = [
      [1, 1],
      [6, 2],
      [3, 3],
      [4, 5],
      [9, 2],
      [2, 4],
      [8, 7],
    ]
    const k = 2
    const expectedClusters = [0, 1, 0, 1, 1, 0, 1]
    expect(KMeans(data, k)).toEqual(expectedClusters)

    expect(
      KMeans(
        [
          [0, 0],
          [0, 1],
          [10, 10],
        ],
        2,
      ),
    ).toEqual([0, 0, 1])
  })

  it('должен выполнить кластеризацию точек на одинаковых расстояниях', () => {
    const dataSet = [
      [0, 0],
      [1, 1],
      [2, 2],
    ]
    const k = 3
    const expectedCluster = [0, 1, 2]
    expect(KMeans(dataSet, k)).toEqual(expectedCluster)
  })

  it('должен выполнить кластеризацию точек в трехмерном пространстве', () => {
    const dataSet = [
      [0, 0, 0],
      [0, 1, 0],
      [2, 0, 2],
    ]
    const k = 2
    const expectedCluster = [1, 1, 0]
    expect(KMeans(dataSet, k)).toEqual(expectedCluster)
  })
})

Запускаем тесты:

npm run test ./algorithms/machine-learning/__tests__/k-means

❯ Статистика

❯ Взвешенная произвольная выборка

Описание

• Что такое взвешенная случайная выборка? ^[34]

Допустим, у нас есть список элементов. Элемент может быть чем угодно. Например, у нас может быть список фруктов и овощей, которые мы любим кушать: [ '🍌', '🍎', '🥕' ].

Список весов представляет вес (вероятность выбора, важность) каждого элемента. Веса — это числа. Например, веса [3, 7, 1] означают следующее:

• мы выбираем яблоко чаще всего (7 из 3+7+1=11 раз)
• банан мы выбираем менее часто (3 из 11 раз)
• морковку мы не любим, поэтому выбираем ее редко (1 из 11 раз)

Если говорить в терминах вероятности, то веса должны быть представлены числами с плавающей запятой, сумма которых дает 1 (например, [0.1, 0.5, 0.2, 0.2]).

Взвешенная произвольная выборка (weighted random) — это функция, которая возвращает произвольный элемент списка с учетом его веса, поэтому элементы с большим весом выбирается чаще.

Пример интерфейса функции:

const items =   [ '🍌', '🍎', '🥕' ];
const weights = [  3,    7,    1  ];

function weightedRandom(items, weights) {
  // Реализация...
}

const nextSnackToEat = weightedRandom(items, weights); // вероятнее всего будет '🍎'

Применение

• в генетической алгоритме ^[35] взвешенная произвольная выборка используется на стадии выборки, когда нам нужно выбрать наиболее приспособленных/сильных особей на основе оценки их приспособленности для спаривания и создания следующего более сильного поколения. См. Самопаркующийся авто за 500 строк кода ^[36]
• в рекуррентных нейронных сетях (RNN) ^[37] при принятии решения о выборе следующей буквы (для формирования предложения) на основе вероятности следующей буквы. См. Jupyter Notebook Recipe Generation using Recurrent Neural Network (RNN) ^[38]
• в балансировщике нагрузки Nginx ^[39] для более частой отправки запросов на сервер с более высоким весом
• во многих других областях

Алгоритм

Самый простой подход состоит в следующем:

1. Дублируем каждый элемент в соответствии с его весом.
2. Выбираем произвольный элемент.

Например, для наших фруктов и овощей можно сгенерировать следующий список:

const items =   [ '🍌', '🍎', '🥕' ];
const weights = [  3,    7,    1  ];

// Дублируем элементы на основе их весов
const weightedItems = [
  '🍌', '🍌', '🍌',
  '🍎', '🍎', '🍎', '🍎', '🍎', '🍎', '🍎',
  '🥕',
];

// Теперь просто извлекаем произвольный элемент из `weightedItems`

Однако, как вы можете видеть, такой подход требует большого количества памяти ^[40] в случае, когда у нас много элементов для повторения. Например, повторение строки "some-random-string" 10 млн раз потребует выделения около 180 Мб памяти только для массива weightedItems.

Более эффективный подход состоит в следующем:

1. Готовим список совокупных весов для каждого элемента (список cumulativeWeights будет иметь такую же длину, как исходный список weights). В нашем случае он будет выглядеть так: cumulativeWeights = [3, 3 + 7, 3 + 7 + 1] = [3, 10, 11].
2. Выбираем произвольное число в диапазоне от 0 до наибольшего совокупного веса. В нашем случае таким диапазоном будет [0...11]. Допустим, мы получили randomNumber = 8.
3. Перебираем cumulativeWeights слева направо и берем первый элемент, который больше или равен randomNumber. Индекс такого элемента используется для выбора элемента из списка items.

Основная идея данного подхода состоит в том, что более высокие веса будут “занимать” больше числового пространства. Таким образом, более высока вероятность выбора произвольного числа из “числовой группы более высокого веса”.

const weights =           [3, 7,  1 ];
const cumulativeWeights = [3, 10, 11];

// `cumulativeWeights` можно представить так
const pseudoCumulativeWeights = [
  1, 2, 3,               // <-- 3 числа
  4, 5, 6, 7, 8, 9, 10,  // <-- 7 чисел
  11,                    // <-- 1 число
];

Реализация

// algorithms/statistics/weighted-random.js
/**
 * Возвращает произвольный элемент на основе его веса.
 * Элементы с более высоким весом выбираются чаще (с большей вероятностью).
 *
 * Например:
 * - items = ['banana', 'orange', 'apple']
 * - weights = [0, 0.2, 0.8]
 * - weightedRandom(items, weights) в 80% случаев будет возвращать 'apple',
 * в 20% случаев - 'orange' и никогда - 'banana' (поскольку вероятность его выбора равна 0%)
 *
 * @param {any[]} items
 * @param {number[]} weights
 * @returns {{item: any, index: number}}
 */
export default function weightedRandom(items, weights) {
  if (!items.length || !weights.length) {
    throw new Error('Элементы/веса не должны быть пустыми')
  }
  if (items.length !== weights.length) {
    throw new Error('Массивы элементов и весов должны иметь одинаковую длину')
  }

  // Готовим массив совокупных весов.
  // Например:
  // - weights = [1, 4, 3]
  // - cumulativeWeights = [1, 5, 8]
  const cumulativeWeights = []
  for (let i = 0; i < weights.length; i++) {
    cumulativeWeights[i] = weights[i] + (cumulativeWeights[i - 1] || 0)
  }

  // Получаем произвольное число в диапазоне [0...sum(weights)].
  // Например:
  // - weights = [1, 4, 3]
  // - maxCumulativeWeight = 8
  // - диапазон произвольного числа - [0...8]
  const maxCumulativeWeight = cumulativeWeights.at(-1)
  const random = Math.random() * maxCumulativeWeight

  // Извлекаем произвольный элемент на основе его веса.
  // Элементы с более высоким весом выбираются чаще
  const index = cumulativeWeights.findIndex((cumulativeWeight) => {
    return cumulativeWeight >= random
  })
  const item = items[index]

  return {
    item,
    index,
  }
}

import weightedRandom from '../weighted-random'

describe('weightedRandom', () => {
  it('при передаче пустого массива элементов или весов должно выбрасываться исключение', () => {
    const getWeightedRandomWithInvalidInputs = () => {
      weightedRandom([], [])
    }
    expect(getWeightedRandomWithInvalidInputs).toThrow(
      'Элементы/веса не должны быть пустыми',
    )
  })

  it('при несовпадении количества элементов и весов должно выбрасываться исключение', () => {
    const getWeightedRandomWithInvalidInputs = () => {
      weightedRandom(['a', 'b', 'c'], [10, 0])
    }
    expect(getWeightedRandomWithInvalidInputs).toThrow(
      'Массивы элементов и весов должны иметь одинаковую длину',
    )
  })

  it('должен правильно выполнять взвешенную произвольную выборку в простых случаях', () => {
    expect(weightedRandom(['a', 'b', 'c'], [1, 0, 0])).toEqual({
      index: 0,
      item: 'a',
    })
    expect(weightedRandom(['a', 'b', 'c'], [0, 1, 0])).toEqual({
      index: 1,
      item: 'b',
    })
    expect(weightedRandom(['a', 'b', 'c'], [0, 0, 1])).toEqual({
      index: 2,
      item: 'c',
    })
    expect(weightedRandom(['a', 'b', 'c'], [0, 1, 1])).not.toEqual({
      index: 0,
      item: 'a',
    })
    expect(weightedRandom(['a', 'b', 'c'], [1, 0, 1])).not.toEqual({
      index: 1,
      item: 'b',
    })
    expect(weightedRandom(['a', 'b', 'c'], [1, 1, 0])).not.toEqual({
      index: 2,
      item: 'c',
    })
  })

  it('должен правильно выполнять взвешенную произвольную выборку', () => {
    // Количество выборок
    const ATTEMPTS_NUM = 1000
    // Погрешность количества выборок элемента.
    // Например, если мы хотим, чтобы элемент 'a' выбирался 300 раз из 1000 (30%),
    // тогда 267 раз является приемлемым, поскольку это больше 250 (300 - 50)
    // и меньше 350 (300 + 50)
    const THRESHOLD = 50

    const items = ['a', 'b', 'c'] // значения элементов неважны
    const weights = [0.1, 0.3, 0.6]

    const counter = []
    for (let i = 0; i < ATTEMPTS_NUM; i += 1) {
      const randomItem = weightedRandom(items, weights)
      if (!counter[randomItem.index]) {
        counter[randomItem.index] = 1
      } else {
        counter[randomItem.index] += 1
      }
    }

    for (let itemIndex = 0; itemIndex < items.length; itemIndex += 1) {
      /*
        Элемент под индексом 0 должен выбираться 100 раз (в идеале)
        или, учитывая порог, [100 - 50, 100 + 50] раз.

        Элемент под индексом 1 должен выбираться 300 раз (в идеале)
        или, учитывая порог, [300 - 50, 300 + 50] раз.

        Элемент под индексом 2 должен выбираться 600 раз (в идеале)
        или, учитывая порог, [600 - 50, 600 + 50] раз
       */
      expect(counter[itemIndex]).toBeGreaterThan(
        ATTEMPTS_NUM * weights[itemIndex] - THRESHOLD,
      )
      expect(counter[itemIndex]).toBeLessThan(
        ATTEMPTS_NUM * weights[itemIndex] + THRESHOLD,
      )
    }
  })
})

Запускаем тесты:

npm run test ./algorithms/statistics

На сегодня это все, друзья. Увидимся в следующей части.

Новости, обзоры продуктов и конкурсы от команды Timeweb.Cloud — в нашем Telegram-канале ^[41] ↩

^[42]