Никто не читает старые статьи… базу, так сказать, основу…
Много авторов так или иначе рассказывают о статьях в ML-сообществе, но большинство из них популярны, потому что являются хорошими опытными специалистами, а значит в своё время прошли все базовые статьи и могут себе позволить рассказывать только о новинках в сообществе. Что же делать молодым специалистам, которые действительно хотят разобраться, но ещё не читали ту самую базу?.. так сказать, основу…
Для себя и, надеюсь, кого-то ещё, я предлагаю эти три разбора, на мой взгляд, основополагающих статей мира ML. Приятного прочтения.

Это мой первый пост на Хабре, не судите строго, но, пожалуйста, судите — с радостью приму любую разумную критику и полезные комментарии. Стоит сказать, что я безумно благодарен сообществу Хабра за все прочитанные мной посты здесь, Вы очень помогаете людям. Спасибо. Надеюсь и я когда-то кому-то помогу.
Разбираем статьи:
Почему именно эти:
-
Символично хотелось начать с Adam, к тому же сам его никогда не читал, уверен что так же, как и многие. А прочитав очень удивился и загорелся этим делом ещё больше.
-
А дальше попытался понять — что именно можно прочитать, что при этом будет полезно и релевантно. Камень в огород The Perceptron, который с колокольни текущего старта знаний ML сообщества кажется рукомаханием.
-
Статья 2 зарождает MLP и является красивой, ёмкой и понятной, то что надо для начала.
-
Статья 3 идейно дополняет 2, доказывая теоретически back-prop. Да, тут уже читается заметно сложнее, но и математикой [4] позаниматься надо иногда.
Если Вы считаете, что всё точно знаете — посмотрите заключение [5], быть может всё же что-то интересное я смог найти в этих статьях и для Вас.
Adam: A Method for Stochastic Optimization
(ICLR 2015)
Submitted on 22 Dec 2014 (v1), last revised 30 Jan 2017 (this version, v9), Читать тут — ArXiv [6]
Diederik P. Kingma — OpenAI, Google, работал над VAE, встретим в статьях в дальнейшем
Jimmy Lei Ba — из популярного — работы над Layer Normalization
✔️ Метод рассчитан на ситуации, когда данных много, а сами градиенты могут быть «шумными» или разреженными. В таких случаях SGD с Momentum далеко не всегда работает оптимально, и возникает мысль об адаптивном подборе шага для каждого параметра (как было в AdaGrad) и об учёте предыдущих градиентов (как в RMSProp). Adam объединяет сильные стороны этих алгоритмов, делая процесс обучения [7] более стабильным и «непривязанным» к слишком тщательному тюнингу гиперпараметров.
✔️ Если коротко, из чего родился Adam:
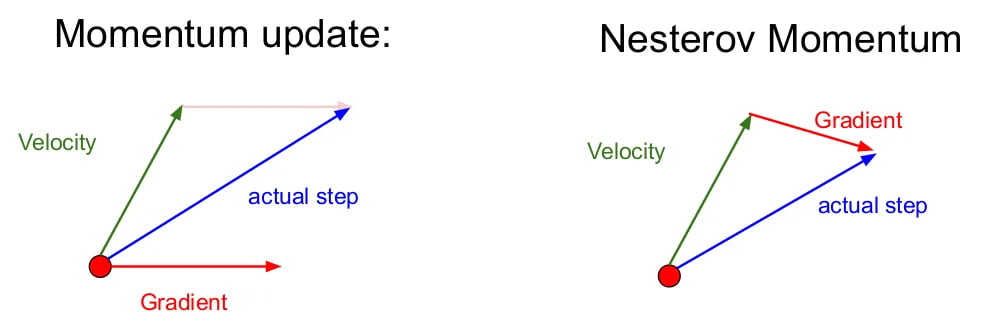
Был GD 🔜 SGD 🔜 Momentum GD (aka «c инерцией») — здесь начну пояснять — предлагается: если мы двигались какое-то время в одном направлении, наверное стоит там же продолжить.
За этим последовал Nesterov Accelerated Gradient, где оценивают градиент «заглянув вперёд», то есть после гипотетического шага, чтобы корректировать движение точнее.
Параллельно появились AdaGrad и RMSProp. AdaGrad делает шаги для тех параметров, что редко получают градиент, относительно больше (что очень полезно при разреженных данных). RMSProp ввёл сглаженную оценку дисперсии градиента, чтобы следить за «шумностью» обновлений.
✔️ Описание предлагаемого метода:
Adam рождается как логическое объединение идей AdaGrad и RMSProp — это знают все, как и то от чего произошло название (Adaptive Momentum).
Однако мало кто упоминает, что важным новшеством стал механизм Initialization Bias Correction. О нём: из-за инициализации моментов нулями — оценки первых итераций оказывались заниженными, а значит градиенты недооценивались. Авторы устранили это, поделив накопленные моменты на 1-β1 и 1-β2 – гиперпараметры отвечающие за «эффект моментума» и сглаживание квадрата градиента. Эти гиперпараметры предлагается выбирать 0.9 и 0.999 соответственно, так что получается именно увеличение значения градиента. Что интересно: формально в статье для доказательства сходимости используется факт уменьшения этих параметров со временем и стремление их к 0, но в реализациях в библиотеках никто не добавляет этот функционал, судя по всему из-за отсутствия существенных улучшений. Благодаря таким «подтянутым» моментам Adam не страдает от заниженных градиентов в начале обучения и ведёт себя более стабильно.
Формулы метода представлены на рис. 2.

✔️Итого мы получаем:
-
Адаптивный подбор шага: каждый параметр обновляется с учётом собственной «истории» градиентов, что особенно выгодно при разреженных данных (в духе AdaGrad) и при шумном обучении.
-
Учёт «моментума»: благодаря компоненте m мы не теряем информацию о направленности векторов градиента, сглаживая колебания.
-
Стабильность от сглаживания второго момента: снижает эффект резких скачков в градиенте и защищает от «взрывных» обновлений.
-
И исправление смещения из-за начальной инициализации.
Если Вы очень внимательный, то заметили, что забыта идея ускоренного метода Нестерова. Хотя в оригинальной статье и предлагается сразу метод AdaMax, он рассматривает лишь использование бесконечной нормы. В дальнейших работах для этого предложен Nadam, учитывающий соответствующее улучшение.
©️Из интересных фактов про работу:
-
Самая цитируемая работа в сфере ML. 210k+ на момент написания текста.
-
Популярная константа Андрея Карпаты — 3e-4. Появилась в твите от 24 ноября 2016 года: “3e-4 — лучший показатель скорости обучения для Adam” следующий твит — “Я просто хотел, чтобы люди поняли, что это шутка…”
-
Куча улучшений, к примеру AdamW (с разделением веса и регуляризации) и AMSGrad (с улучшенной сходимостью).
Learning Representations by Back-Propagating Errors
David E. Rumelhart — Когнитивный психолог, Stanford
Geoffrey E. Hinton — Тьюринговский лауреат 2018, Нобелевская премия 2024, CMU
Ronald J. Williams — Автор метода REINFORCE, CMU
(вышла в журнале Nature, 9 октября 1986)
Читать тут [8]
✔️ Предпосылки
До 1986 года нейросети обучались в основном на однослойных моделях, и было ясно, что для более сложных задач нужно больше слоёв. Но как обучать такие сети, если ошибки [9] должны передаваться обратно через несколько слоёв?
Авторы предложили революционное решение, которое мы теперь знаем как обратное распространение ошибки (back-propagation). Также они показали на красивых экспериментах работоспособность метода. В процессе экспериментов был предложен первый вариант Momentum-SGD, а также проинтерпретированы скрытые состояния — заучивание промежуточных признаков.
✔️ Описание метода
Метод заключается в том, что ошибки, возникающие на выходе нейросети, передаются обратно, чтобы корректировать веса всех слоёв. Важнейший элемент — это цепное правило для дифференцирования, которое позволяет вычислить ошибки для каждого слоя.
Основные шаги метода: (рис. 3.)
-
Прямой проход (Forward):
-
входные данные проходят через все слои сети
-
на выходе получаем предсказания
-
-
Обратный проход (Backward)
-
Повторяем [10] процесс, минимизируя ошибку

Рис. 3. Примерное описание предлагаемого метода обучения MLP
✔️ Эксперименты
-
Симметрия [11]
MLP (6-4-1) получает 6-битный вектор и должна ответить симметричен/не симметричен относительно центра. Без скрытых узлов задача нерешаема. Два скрытых нейрона [12] «научились» включаться только при симметричных паттернах, показав, что back-prop действительно вырабатывает внутренний признак симметрия (рис. 4)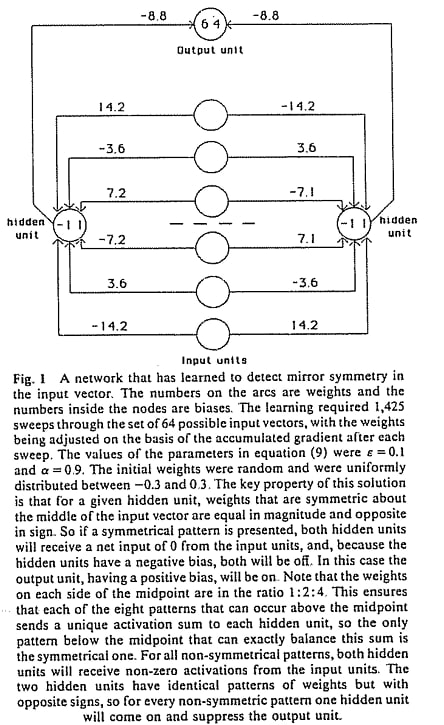
Рис. 4. Эксперимент из оригинальный статьи -
Множественность и сложные признаки
Представлен эксперимент с пятислойной сетью, которая анализировала семейные связи. В результате эксперимента получено, что промежуточные слои научились распределённым признакам: ни один нейрон [13] не отвечает за конкретного человека, вместо этого паттерн активности кодирует сложный признак — англичанин/итальянец, поколение, ветка и т. д.
(рис. 2,3,4 из оригинальной статьи, не решился вставлять.)
✔️ Интересные факты
-
Объём — всего 4 страницы, в которых 3 эксперимента с 6 картинками, минимум формул и никакого теоретического вывода.
-
Хинтон написал рабочий LISP-код за выходные, попробовал обучить автоэнкодер (8-3-8-битный — ожидалось, что скрытый слой — битовое представление числа), но получил «кашу» в активациях (не похоже на двоичную структуру, как в больцман-машинах) и уже решил, что алгоритм сломан, пока не заметил, что ошибка = 0: «Я чуть не похоронил back-prop, не поняв, что он уже выучил».
A Theoretical Framework from Back-Propagation
Yann LeCun, 1988, читать тут [14]
об авторе:
Тьюринговский лауреат (2018)
Из наиболее известного кроме множества работ по BackProp — автор LeNet-5
✔️ Предпосылки
К 1986 г. Rumelhart & Hinton показали «рецепт» обратного распространения ошибки, но:
-
формального вывода не было — алгоритм воспринимали как «трюк цепного правила»
-
сложность вычислений оценивали приблизительно
-
применяли почти только к перцептронам с сигмоидами
✔️Описание предлагаемого метода:
Оно представлено в картинках, ещё и в чуть упрощённом виде, адаптированном под современное использование Лагранжиана. В оригинале много формул и подробностей, а телеграмм не позволяет это писать в адекватном виде…
Очень рекомендую к ознакомлению, вроде бы каждый знает что back-prop это там forward/backward, chain rule и все дела, а на деле оказывается что да – так его придумали, но начали везде использовать только когда вот автор через Множители Лагранжа доказал!


✔️ Дополнительные идеи представленные в работе
-
Честная оценка сложности — O (2|E|)
-
Целый параграф про continuous-time recurrent networks, предки современных Neural-ODE. По сути аналогичный вывод, но теперь доказана работоспособность back-prop для рекуррентных систем с непрерывным временем.
-
Задел в будущее — weight sharing В то время фильтры в CNN не умели обучать по многим причинам, одна из них – память… Для решения этого вопроса придумали что фильтры могут принимать только конкретный пул значений LeCun доказал, что в этой постановке можно использовать back-prop и обновление общего повторяющегося фильтра получается как сумма вкладов от каждой позиции. Но работы было видимо ещё много, LeNet-5 выпустили только через 10 лет
©️ Интересное:
-
Появилась в материалах летней школы Connectionist Models, причём изначально не как статья, а как короткий лекционный конспект.
-
Заметки/обзор на английском с красивым сравнением обычного вывода и через Лагранжа — тут [15].
Заключение
-
В статье Adam’14 неожиданно нашли Initialization Bias Correction. Также узнали, что без него метод не обязан сходиться, несмотря на это – все стандартные библиотеки не реализуют эту поправку.
-
В статье Rumelhart & Hinton’86 прочитали как зародились MLP и метод back-prop. Также увидели первую версию Momentum-SGD
-
В статье LeCun’88 — увидели красивый вывод back-prop через Лагранжиан, а также зарождение convolution и continuous-time recurrent нейросетей.
Спасибо за прочтение. Надеюсь хоть кто-нибудь окажется на этом моменте)
Если вдруг Вам понравился этот текст, то быть может будет интересен и мой телеграм-канал [16] с другими разборами и материалами. До новых встреч!
Автор: Schaft
Источник [17]
Сайт-источник BrainTools: https://www.braintools.ru
Путь до страницы источника: https://www.braintools.ru/article/16107
URLs in this post:
[1] Adam: A Method for Stochastic Optimization: #adam_id
[2] Learning Representations by Back-Propagating Errors: #hinton_back_prop_id
[3] A Theoretical Framework from Back-Propagation: #lecun_back_prop_id
[4] математикой: http://www.braintools.ru/article/7620
[5] заключение: #end
[6] ArXiv: https://arxiv.org/abs/1412.6980
[7] обучения: http://www.braintools.ru/article/5125
[8] Читать тут: https://www-edlab.cs.umass.edu/cs697l/readings/Learning%20representations%20by%20back-propagating%20errors.pdf
[9] ошибки: http://www.braintools.ru/article/4192
[10] Повторяем: http://www.braintools.ru/article/4012
[11] Симметрия: http://www.braintools.ru/article/3088
[12] нейрона: http://www.braintools.ru/article/6020
[13] нейрон: http://www.braintools.ru/article/9161
[14] читать тут: https://www.researchgate.net/publication/2360531_A_Theoretical_Framework_for_Back-Propagation
[15] тут: https://wordpress.cs.vt.edu/optml/2018/04/28/backpropagation-is-not-just-the-chain-rule/
[16] телеграм-канал: https://t.me/schafts
[17] Источник: https://habr.com/ru/articles/917664/?utm_campaign=917664&utm_source=habrahabr&utm_medium=rss
Нажмите здесь для печати.