От нестационарности к прогнозу: пайплайн анализа и моделирования временных рядов

Я Михаил Зуев — Data Scientist из команды расходов корпоративного и инвестиционного бизнеса Сбера. Мы много предсказываем, классифицируем и прогнозируем. Впервые столкнувшись с последним и проведя исследование по этой теме, я столкнулся с большим количеством неструктурированной информации. Эта статья — одновременно описание моего пути и небольшое упорядоченное наставление по анализу и прогнозированию временных рядов, которое я сам хотел бы получить.

Начнём с теории.

Временной ряд (он же time series) — это последовательность упорядоченных во времени числовых показателей, характеризующих уровень состояния и изменения изучаемого явления

[Афанасьев, В.Н. Анализ временных рядов и прогнозирование: учебник / В.Н. Афанасьев, М.М. Юзбашев — М.: Финансы и статистика, 2001. — 228 с]

Графическое представление такого ряда:

import pandas as pd
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
plt.plot(y['Месяц'], y['Сумма'], color='orangered')
plt.title(f'Исходный ряд')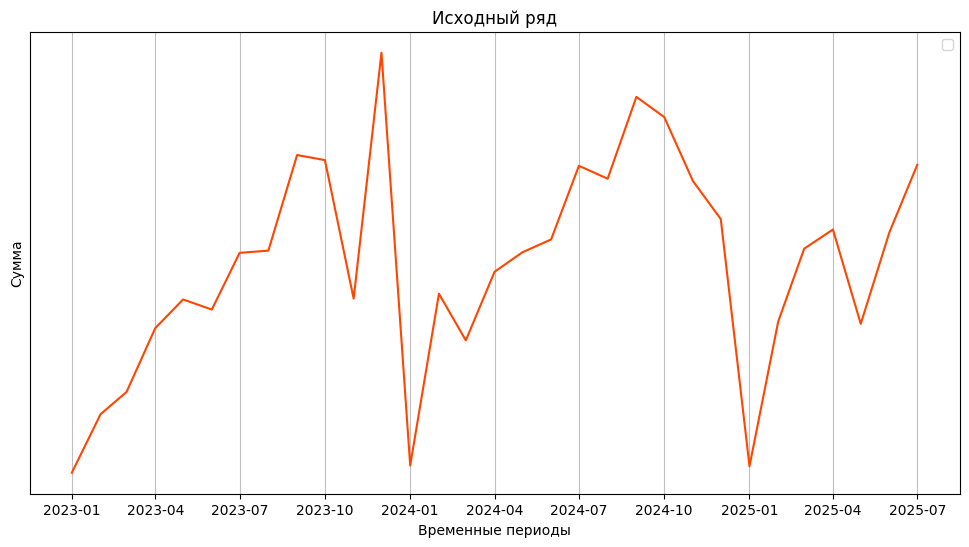

Одна из важных характеристик ряда — его тренд. Это такая зависимость, которая позволяет посмотреть на имеющийся ряд с прогнозной точки зрения ^[1]: есть ли тенденция увеличения некоторого показателя со временем? Если да, то какая? Знание об этом факте позволяет делать первые предположения о прогнозе.

Ещё выделяют сезонность — циклическое изменение уровня ряда с постоянным периодом (повторением ^[2] в определённые моменты времени). Применительно к графику выше можно сказать, что некоторые суммы люди с большой неохотой тратят по январям (наступают новогодние праздники), причём этот спад повторяется три года подряд. Это и есть сезонность.

Нельзя не учесть и влияние случайных колебаний — непрогнозируемого случайного изменения ряда, не имеющего тенденции к постоянству, которое всё‑таки влияет на то, каким получается наш ряд.

Чтобы не на словах, а статистически увидеть тренд, сезонность и случайные колебания, применим функцию seasonal_decompose() из библиотеки Statsmodels для Python:

from statsmodels.tsa.seasonal import seasonal_decompose

fig, axes = plt.subplots(4, 1, figsize=(12, 8))
y = y.set_index('Месяц')
decompose = seasonal_decompose(y, period=12)
y.plot(ax=axes[0], title='Исходные данные')
decompose.trend.plot(ax=axes[1], title='Тренд')
decompose.seasonal.plot(ax=axes[2], title='Сезонность')
decompose.resid.plot(ax=axes[3], title='Шум')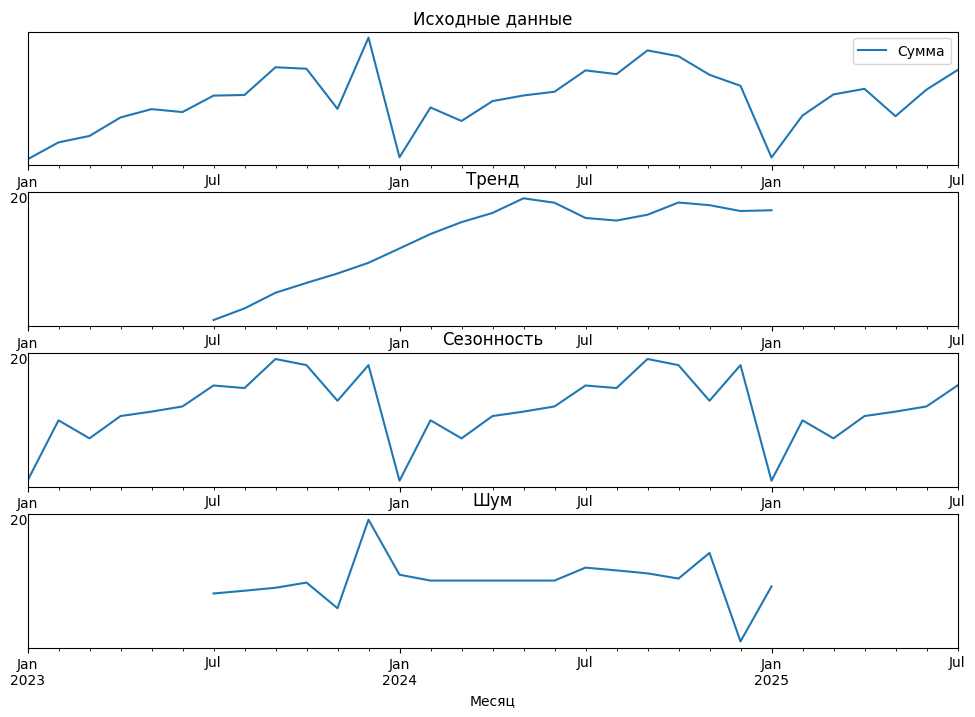

Судя по графику, наблюдается явный тренд на увеличение, затухающий примерно в мае 2024, сезонность с ярко выраженными спадами в январе, зашумленность с декабрьскими пиком 2023 года (максимум) и 2024 года (минимум).

В случае единственного графика такой простой визуальный анализ может сработать, но графиков может быть много, а потребность ^[3] в их анализе — быстрой. В этом случае применяют статистическую оценку, то есть такие тесты, которые позволят однозначно выявить факт стационарности или нестационарности. Нестационарность — это свойство временного ряда, которое выражается в изменении с течением времени статистических характеристик, таких как математическое ожидание и дисперсия. Примеры подобных рядов:

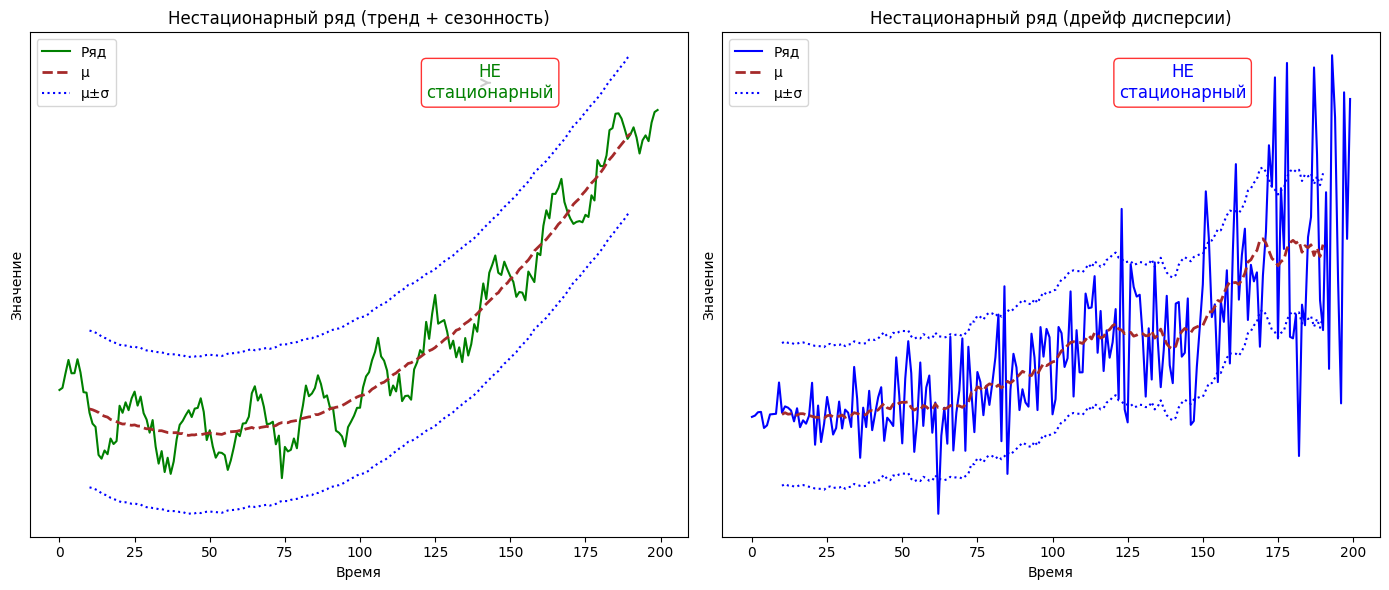
Нестационарные временные ряды трудно поддаются моделированию и прогнозированию, поскольку результаты, полученные с их использованием, часто оказываются ложными: анализ выявляет несуществующие зависимости и закономерности. Для получения корректных и надёжных результатов анализа нестационарные временные ряды необходимо преобразовать в стационарные.

Чтобы явно сказать, к какому типу рядов относится наш ряд, мы применяем статистические тесты на определение стационарности или нестационарности. Я пользовался расширенным тестом Дики‑Фуллера (ADF) (самым распространённым, но не единственным методом оценки). В очень широком смысле ADF‑тест определяет, является ли временной ряд стационарным, проверяя нулевую гипотезу о том, что в ряду присутствует единичный корень, что указывает на нестационарность. Если на выходе p‑value > 0.05, то гипотеза принимается как верная — ряд нестационарен, и наоборот при p‑value <= 0.05. Это даёт нам чёткое представление о том, стоит ли дифференцировать ряд для приведения к стационарности.

from statsmodels.tsa.stattools import adfuller
adf_result = adfuller(y)
print(f'p-value по Дики-Фулеру: {adf_result[1]:.4f}')

# p-value по Дики-Фулеру: 0.3856

Полученное p-value оказалось значительно выше 0.05, следовательно, нулевая гипотеза принимается — ряд нестационарен. И действительно: наличие сезонности и некоторого тренда на графиках выше этому подтверждение. Теперь перейдём к самому интересному — алгоритмам прогнозирования.

AR: как прошлое предсказывает будущее (и почему это не магия)

Представьте: вы хотите спрогнозировать, сколько пользователей зайдёт на ваш сервис завтра. У вас нет внешних данных — ни рекламы, ни праздников, ни погоды. Только история: сколько заходило вчера, позавчера и неделю назад. И тут приходит идея: «А что, если будущее уже закодировано в прошлом?» Именно на этом строится авторегрессионная модель  — один из самых старых, но до сих пор актуальных инструментов анализа временных рядов.

Модель авторегрессии порядка (обозначается как ) утверждает:

Сегодняшнее значение = взвешенная сумма p предыдущих значений + шум.

Формально:

где:

• — значение ряда в момент (например, продажи в день );

• — коэффициенты авторегрессии, которые показывают, насколько сильно каждое из p предыдущих значений влияет на текущее;

• — порядок модели , то есть количество лагов (прошлых значений ряда), учитываемых в модели;

• — гауссовский белый шум в момент .

Интуитивно это можно понять так: если , то вчерашнее значение сильно влияет на сегодняшнее. Если  — почти не влияет.

И ещё, если модель обозначается как , то это значит, что она учитывает три
предыдущих значения:

Модель проста, понятна и удобна, если спрос ведёт себя стабильно. Она не требует сложных вычислений и часто используется в прогнозировании как базовая модель. Но если значение ряда резко меняется — из‑за акций, праздников, замены товара на аналог, то такая модель может сильно ошибаться. А у нас как раз наблюдается сезонность.

MA (Moving Average): «Я ошибся — и это полезно»

Представьте: вы прогнозировали продажи на вчерашний день. Реальность оказалась на 100 единиц выше. Эта разница — не просто статистический шум. На самом деле, именно такие отклонения лежат в основе одной из ключевых моделей временных рядов — , или модели скользящего среднего (Moving Average).

Но обратите внимание ^[4]: ≠ скользящему среднему в привычном понимании сглаживания данных. Это распространённое заблуждение. Давайте разберёмся, почему.

Модель порядка выглядит так:

где:

• — значение ряда в момент (аналогично );

• — коэффициенты -части. Показывают, насколько сильно прошлые шоки влияют на текущее значение;

• — порядок модели , то есть количество прошлых ошибок (шоков),
  учитываемых в модели;

• — гауссовский белый шум в момент .

Вот в чём ключевая идея: модель MA не сглаживает данные, как привычная скользящая средняя на графике. Вместо этого она моделирует текущее значение через прошлые ошибки ^[5] прогноза. То есть, если вчера вы ожидали продажи на 500 единиц, а продали 600, то разница (+100) становится шумом . И сегодня, в момент , эта «ошибка» может всё ещё влиять на реальные продажи: например, из‑за остатков рекламной активности, переполненного склада или просто инерции спроса.

Именно поэтому в модели нет ,  — только , и прочие шумы. Это не авторегрессия, когда прошлое значение тянет за собой будущее. Это своеобразная «память» об ошибках: рынок (или система) «помнит», насколько мы вчера промахнулись, и корректирует текущий расчетный момент.

ARMA: когда прошлое и ошибки работают в паре

Представьте, что вы — дирижёр оркестра временных рядов. Слева — скрипки (авторегрессии): они повторяют мелодию прошлого, потому что «всё, что было, влияет на то, что будет». Справа — виолончели (скользящего среднего): они играют аккорды на основе того, насколько вы ошиблись в предыдущих тактах.

А теперь вы поднимаете дирижёрскую палочку. И звучит  — гармония памяти ^[6] и коррекции.

Формально модель выглядит так:

где:

• — порядок авторегрессионной части;

• — порядок части скользящего среднего.

Объединение этих методов работает потому, что реальные процессы редко бывают только инерционными (как AR) или только реактивными применительно к ошибкам (как MA). Чаще бывает и то, и другое. ARMA учитывает оба этих эффекта в одном уравнении. Важный нюанс: ARMA требует стационарности, которой наш ряд не обладает.

ARIMA не верит в Новый Год. SARIMA — да

ARMA работает только со стационарными рядами, а реальные данные растут и падают по сезонам. , расширение , обходит это просто: вместо исходного ряда она моделирует порядок его разности порядка (например, ), делая его стационарным, а потом применяет обычную ARMA.

Но что, если помимо тренда у вас есть сезонность? Как видно из нашего графика, некоторая величина неуклонно падает каждый январь. Обычная не предназначена для эффективного моделирования выраженной сезонности — для этого существует её сезонное расширение: .

На помощь приходит  — Seasonal . Она добавляет к обычным параметрам сезонный блок (P, D, Q)_, где — период (например, 12 для месячных данных). Теперь модель учитывает не только то, что было вчера, но и то, что было ровно год назад, и делает это через сезонные разности и сезонные лаги.

Именно эта модель подходит в нашем случае:

• она учитывает сезонность через дополнительные параметры и период (для месячных данных);

• позволяет моделировать как тренд, так и сезонные циклы (например, январские спады и декабрьские пики).

Для автоматического подбора оптимальных параметров воспользуемся функцией auto_arima из библиотеки Pmdarima (обёртка над Statsmodels):

from pmdarima import auto_arima
from statsmodels.tsa.statespace.sarimax import SARIMAX

stepwise_fit = auto_arima(y['Сумма'], # Данные для обучения
                          m = 12, # Длина сезона
                          seasonal = True, # Указываем на наличие сезонности
                          trace = True, # Вывод отладочной информации
                          error_action ='ignore', # Игнорим ошибки
                          suppress_warnings = True) # Подавление предупреждений

order = stepwise_fit.order
seasonal_order = stepwise_fit.seasonal_order
sarimax_model = SARIMAX(y_train['Сумма'],
                        order=order, # Передаем параметры после auto_arima
                        seasonal_order=seasonal_order) # Передаем параметры после auto_arima
sarimax_fit = sarimax_model.fit()
predictions = sarimax_fit.forecast(steps=29) # Прогноз

Затем визуализируем прогноз на фоне реальных данных:

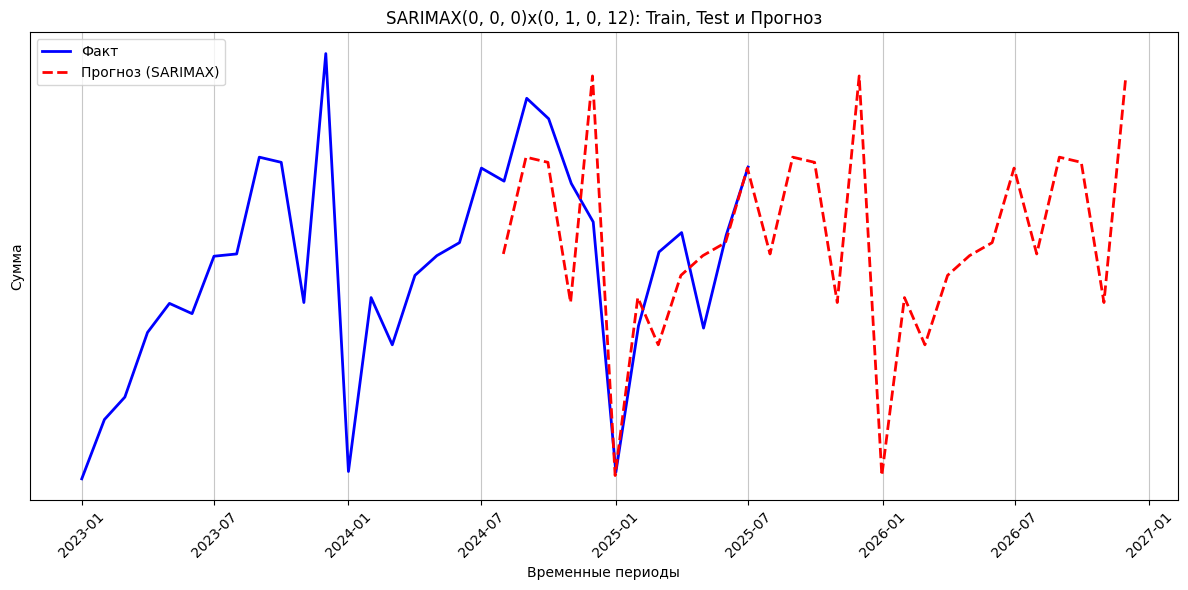
Результаты:

• Модель точно воспроизвела сезонные паттерны: спады в январе и рост к концу года.

• Прогноз незначительно завышен относительно предыдущего года, что соответствует бизнес‑требованию о повышении суммы за год не больше, чем на индекс инфляции.

• Ошибки прогноза на тестовом периоде оказались в допустимых пределах (MAPE ≈ 8,2%).

Выводы:

• Анализ структуры ряда (тренд, сезонность, стационарность) — обязательный этап перед выбором модели.

• Статистические тесты (например, ADF) надёжнее визуальной оценки при определении стационарности.

•  — мощный инструмент для рядов с выраженной сезонностью и трендом.

• Автоматизация подбора параметров (auto_arima) значительно ускоряет эксперименты и снижает порог входа.

Эта статья — не истина в последней инстанции, а отчёт о моём пути. Буду рад вашим ценным советам, замечаниям и альтернативным подходам!