Почему линейная регрессия всё ещё обыгрывает трансформеры в анализе временных рядов

На волне успеха ИИ в языке, изображениях и видео многие надеялись, что трансформеры помогут и прогнозированию временных рядов. Реальность чаще прозаична: простая линейная регрессия нередко бьет громоздкие модели по среднеквадратичной ошибке ^[1]. Рассматриваемое исследование аккуратно и строго объясняет, почему так происходит, если смотреть на задачу через призму in-context обучения ^[2].

В авторской постановке вход — это не просто история наблюдений, а матрица Ханкеля из окон длины p+1, где последняя строка специально «зарезервирована» под будущий ответ. Над этой матрицей работает линейное самовнимание (LSA) — упрощенная версия без softmax, зато с чистой математикой ^[3]. Прогноз считывают из зарезервированного «слота». Выгода подхода в том, что он отбрасывает лишние детали и позволяет увидеть пределы выразительности прямо в формулах.

Что скрывается под капотом внимания

Авторы показывают: один слой LSA — это линейный функционал от кубических признаков входной последовательности. Звучит богато, но именно эти признаки в стационарных авторегрессиях постепенно «схлопываются» к последним p лагам. То есть при длинном контексте лучшая LSA-предсказательная функция фактически совпадает с обычной p-лаговой линейной регрессией. Внимание ^[4] не извлекает принципиально новый сигнал — оно лишь переупорядочивает и пересмешивает уже доступную линейную информацию.

Строгий разрыв при конечной истории

Главная интрига — в конечной длине контекста. Теория дает немалоприятный результат: даже оптимально настроенный LSA при любом фиксированном числе наблюдений будет иметь ожидаемую MSE строго выше, чем классический линейный предиктор по p лагам. Этот зазор структурный, а не следствие неудачной тренировки, и убывает не быстрее, чем 1/n. Увеличение глубины (больше слоев LSA) помогает, но насыщается — можно «догнать» линейную регрессию асимптотически, но «обогнать» при конечном n нельзя.

Куда утекает точность при многошаговом раскручивании

В реальном прогнозе важны не только один шаг вперед, но и последовательные шаги. Здесь авторы рассматривают Chain-of-Thought: модель по шагам дописывает свои же предсказания и идет дальше. Для AR(p) это приводит к экспоненциальному «стягиванию» прогноза к среднему значению процесса по мере роста горизонта. Даже идеальный байесовский линейный предс��азатель имеет растущую ошибку с горизонтом, но LSA стартует хуже уже на первом шаге и потому проигрывает на всех последующих. Отсюда практическая рекомендация: не переоценивать длинные CoT-цепочки в прогнозировании рядов — ошибки неизбежно накапливаются.

Как это выглядит на данных

Авторы подтверждают теорию синтетическими экспериментами на AR-процессах. При teacher forcing линейная регрессия стабильно лучше LSA; при CoT обе модели со временем «сползают» к среднему, но LSA ломается раньше. Масштабирование длины истории и глубины слоев улучшает LSA, однако разрыв от линейной базы сохраняется и лишь медленно закрывается.

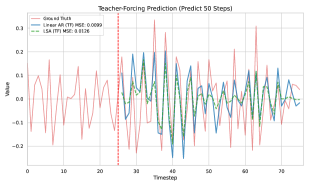
А как насчет softmax-внимания?

В дополнении авторы сравнивают LSA и классическое softmax-внимание в одинаковых условиях. Softmax чуть сильнее эмпирически, что логично ^[5]: у него выше выразительность. Но принципиальный вывод не меняется — даже в этой версии трансформер не переигрывает линейную базу на AR-процессах.

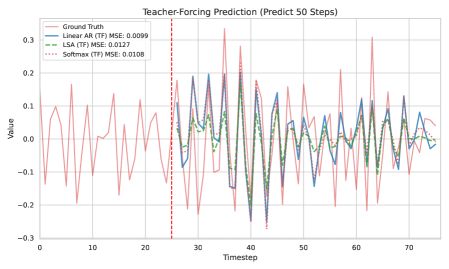
Что всё это значит

• Всегда держите линейный базовый прогноз под рукой. Если данные близки к AR/ARMA, он задает «планку», которую самовнимание не обязано превышать.

• Длинный контекст полезен, но чудес не совершает: разрыв закрывается медленно, примерно как 1/n.

• Глубина слоев без дополнительных блоков не спасает. Временной сигнал в таких рядах преимущественно локален; без сильных нелинейных слоев или профильных архитектур выигрыш ограничен.

• Осторожнее с многошаговыми CoT-сценариями: ошибки копятся и тянут прогноз к среднему раньше, чем хочется.

• Если ряды сложнее линейных (режимы, сезонность, экзогенные факторы), стоит смотреть в сторону гибридов: линейные головы плюс нелинейные блоки, стохастические модели состояний, либо частотные и сезонные декомпозиции.

Почему выводы важны

Работа аккуратно отделяет вопросы оптимизации от ограничений представимости. Даже в идеальных условиях, с правильно подобранными весами, LSA на AR(p) не способен систематически обогнать традиционные линейные предикторы. Это объясняет, почему на реальных датасетах трансформеры нередко выигрывают лишь после добавления сильных нелинейных компонент и предметных индуктивных предубеждений, а иногда и вовсе уступают простым методам.

📜 Полная статья ^[6]

💾 Код ^[7]

***

Если вам интересна тема ИИ,  ^[8]подписывайтесь на мой Telegram‑канал ^{[9]  [10]}— там я регулярно делюсь инсайтами по внедрению ИИ в бизнес, запуску ИИ-стартапов и объясняю, как работают все эти ИИ-чудеса.