Долгая дорога к DiT (часть 2)

Новая задача

Продолжаем то, на чём остановились в первой части. Напомню, нам удалось создать модель, которая может трансформировать простое (нормальное) распределение в целевое. Вот только работала она лишь с точками на плоскости, иными словами, в пространстве тензоров с шейпом (2). Короче, это была лишь тренировка на простых данных (2-размерных векторах). Надо браться за что-то посерьезнее. Как насчёт того, чтобы замоделировать превращение нормального распределения в изображения цифр и букв? Для такого как раз есть подходящий датасет – EMNIST называется. Содержатся в нём чёрно-белые изображения размером 28×28 пикселей. Так что сэмплы (выборки) целевого распределения это уже не две точки представленные тензором с шейпом (2), а целая картинка, представленная уже тензором (28, 28).

Задача опять та же: Мы хотим извлекать сэмплы из целевого распределения (узнаваемые черно-белые изображения), но просто так взять и получить изображение мы не можем, зато можем научить нейросеть трансформировать нормально распределение (шум) в целевое (картинки из датасета EMNIST). И как только мы натренируем такую нейросеть, мы сможем генерить бесконечное количество картинок – достаточно просто взять сэмпл из нормального распределения, и прогнать его через нашу модель. Давайте перефразирую: Если модель способна трансформировать распределение А в распределение В, то это значит, что, имея в распоряжении сэмпл распределения А, можно, используя эту модель, получить сэмпл из распределения В. В нашем случае распределение А – это гауссовый шум, сэмлпы которого очень просто получить, а распределение В (целевое) – это черно-белые изображения букв и цифр.

Кривой датасет

Пора поближе познакомиться с датасетом. На этот раз мы не создаём его сами, а просто скачиваем полгигабайта из интернета:

from torchvision.datasets import EMNIST

dataset = EMNIST(
    root="./emnst",  # в какую папку сохранять
    split="balanced",  # часть датасета
    download=True,  # если False, то будет ожидать что датасет уже скачен
)

Параметр split="balanced" означает, что датасет будет содержать только часть классов. Погодите, что ещё за “классы”? Сейчас объясню. Дело в том, что датасет это не просто набор картинок, это набор пар текст -> изображение. Вот этот текст и называется class или label. В датасете EMNIST классы – это просто буквы и цифры, например:

"j" -> image_1
"j" -> image_2
"a" -> image_3
...

Вот только класса “j” в нашем датасете не будет – мы выбрали вариацию “balanced”, в котором изображения, привязанные к каждому классу должны выглядеть уникально. Например, убран класс “o”, ведь уже есть класс “O”, выглядящей идентично. Только не стоит забывать ^[1], что когда мы запрашиваем данные из датасета, то возвращает он нам не сами значения классов, а их индексы.

Давайте уже посмотрим из чего состоит этот датасет. Просто вытягиваем сэмплы, обращаясь к датасету по индексу:

# Готовимся показать 4 картинки в ряд
fig, plots = plt.subplots(1, 4, figsize=(16, 4))
for i in range(4):
    image, clazz = dataset[i]  # Я же говорил, что датасет состоит из пар
    plots[i].imshow(image)
plt.show()

Если что, plt взялся вот отсюда:

import matplotlib.pyplot as plt

PyPlot – это удобная библиотека для визуализации. Она ещё и с Numpy и PyTorch совместима. И привыкайте к plt.subplots– в статье такого будет много.

Вызвав этот код у нас на экране появится вот такое изображение сэмпла из датасета EMNIST:

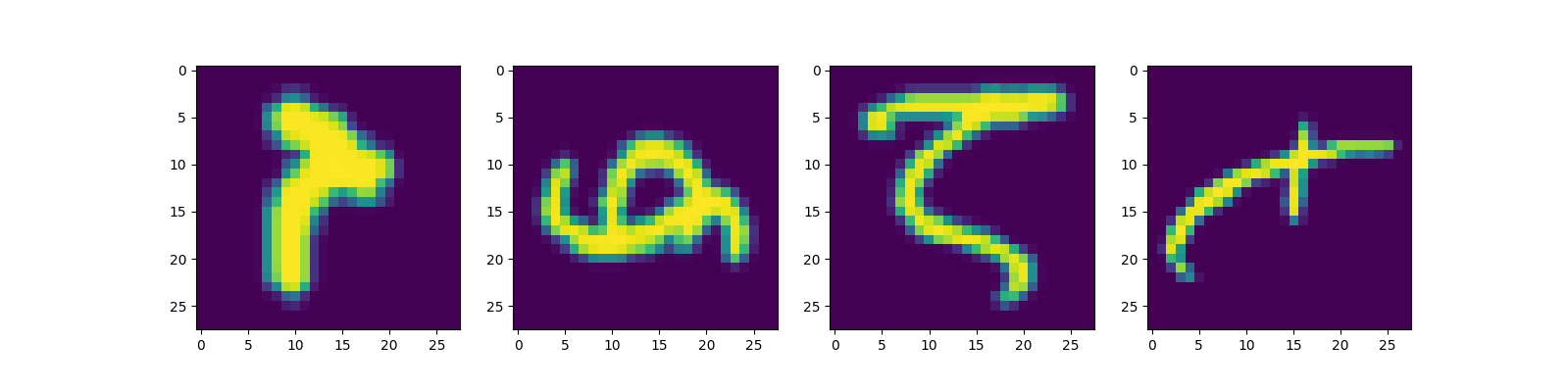
Шкала тут явно не к месту, так что давайте её уберём. Заодно и цвет поменяем:

fig, plots = plt.subplots(1, 4, figsize=(16, 4))
for i in range(4):
    image, clazz = dataset[i]
    plots[i].imshow(image, cmap="gray")  # цвет неба - серый
    plots[i].axis("off")  # отключить
plt.show()

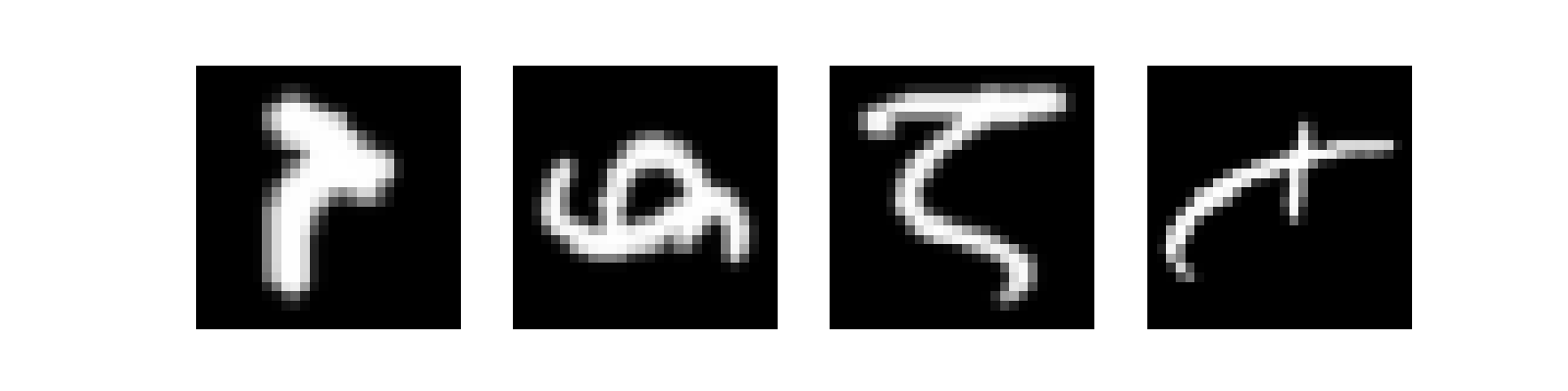
Выглядит хорошо, но кажется осталась проблема. Проблема в том, что сэмплы из датасета криво отображаются! А знаете почему? Потому что эти буквы по умолчанию отзеркалены и повёрнуты на 90 градусов.

Этого так оставлять нельзя, надо их “раскрутить” обратно. По счастью, при работе с torchvision датасетами, можно передать им “инструкцию” о том, как трансформировать каждый сэмпл:

dataset = EMNIST(
    root="./emnst", 
    split="balanced", 
    download=True, 
    transform=transforms,  # указываем как модифицировать (аугментировать) сэмплы
)

А откуда transform возьмётся? Из этого объявления:

from torchvision.transforms import v2 as T  # версия 2, ага

transforms = T.Compose([  # группа последовательных трансформаций
	# выбираем случайный угол поворота между -90 и -90 градусов.
    T.RandomRotation(degrees=(-90, -90)),  
    T.RandomHorizontalFlip(p=1),  # с вероятностью 100% зеркалим сэмпл
    T.ToTensor()  # и сразу в тензоры конвертируем, чтобы 2 раза не вставать
])

И не надо удивляться RandomRotation и RandomHorizontalFlip, ведь основное предназначение torchvision.transforms – это аугментация изображений. Ну то есть для того, чтобы искусственно увеличить датасет. Например, представьте, что у нас есть датасет из фотографий, но нам его мало, так как данных всегда мало. Что мы можем сделать? Мы можем искусственно “раздуть” датасет в два раза, если отразим каждую фотографию по горизонтали. Правда, на фотографиях городских пейзажей все надписи получатся отзеркаленными, но вот изображения природы зеркалить можно без проблем. А ещё можно crop делать. Загляните в документацию ^[2], если интересно.

А сейчас нам интересно на то как теперь выглядят изображения из датасета. Запускаем скрипт и..

TypeError: Invalid shape (1, 28, 28) for image data

Ну вот, imshow(image, cmap="gray") не хочет рисовать наши сэмплы. А виной всему вот эта строка:

T.ToTensor()

Тут дело в том, что при работе с изображениями PyTorch ожидает, что изображение будет представлено тензором вот с таким шейпом: (C, H, W). Давайте поясню, что означает здесь каждый символ:

• C (channel) – это количество каналов. Для RGB-изображения каналов будет 3, для RGBA их будет 4 (красный, зелёный, синий и альфа-канал для прозрачности), а в нашем случае всего 1, так как изображение чёрно-белое.

• H (height) – высота (всегда идёт прежде чем ширина).

• W (width) – ширина (всегда после высоты).

Трансформатор ToTensor преобразует черно-белые изображения 28×28 из датасета MNIST в тензоры с шейпом (1, 28, 28). Мы передаём такое изображение функции imshow, но imshow может рисовать чёрно-белые изображения только если мы ему передадим тензор с шейпом (H, W) либо с шейпом (H, W, C). В общем, мы имеем на руках тензор с шейпом (C, H, W) – конкретно (1, 28, 28), а хотим получить тензор шейпом (H, W, C) – то есть (28, 28, 1). Количество элементов остаётся неизменным, просто элементы по-другому “упакованы”. На самом деле, довольно банальная операция для PyTorch. Всего-то делов вызвать

image.permute(1, 2, 0)  # возвращает тензор с измененным порядком dimensions

Теперь всё работает без ошибок. Давайте сравним сэмплы до и после трансформации:

Было, стало (гифка)

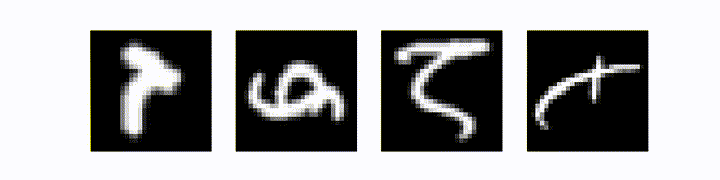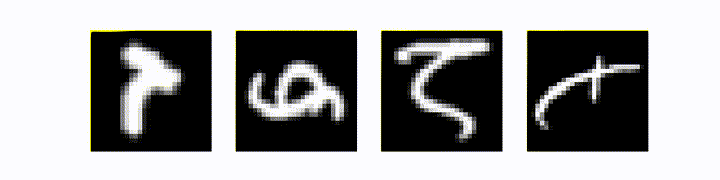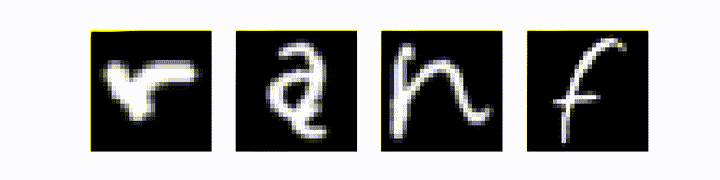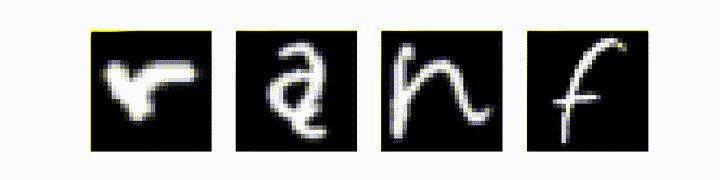
Полный код:

import matplotlib.pyplot as plt
from torchvision.datasets import EMNIST
from torchvision.transforms import v2 as T

transforms = T.Compose([
    T.RandomRotation(degrees=(-90, -90)),
    T.RandomHorizontalFlip(p=1),
    T.ToTensor()
])

dataset = EMNIST(
    root="./emnst",  # в какую папку сохранять
    split="balanced",  # часть датасета
    download=True,  # если False, то будет ожидать что датасет уже скачен
    transform=transforms,  # указываем как модифицировать (аугментировать) сэмплы
)

# Готовимся показать 4 картинки в ряд
fig, plots = plt.subplots(1, 4, figsize=(16, 4))
for i in range(4):
    image, clazz = dataset[i]
    plots[i].imshow(image.permute(1, 2, 0), cmap="gray")
    plots[i].axis("off")
plt.show()

Приступаем к тренировке

Ладно, датасет скачали, сэмплы посмотрели. Пора использовать данные по назначению – натренировать модель.

Переиспользуем тренировочный код из прошлой статьи, внеся правки под новый датасет и модель:

BATCH_SIZE = 256
LR = 6e-4
DEVICE = 'cuda'
EPOCHS = 600

data_loader = torch.utils.data.DataLoader(
    dataset=dataset,
    batch_size=BATCH_SIZE,
    shuffle=True,
)
optimizer = torch.optim.AdamW(model.parameters(), lr=LR)

for epoch in range(EPOCHS):
    epoch_loss = 0
    for x0, clazz in data_loader:
        x0 = x0.to(DEVICE)
        clazz = clazz.to(DEVICE)
        time = torch.rand((x.size(0), 1), device=DEVICE)

        noise = torch.randn_like(x, device=DEVICE)

        true_velocity = x0 - noise
        # Помните, чем больше time, тем больше шума
        xt = x0 * (1 - time) + noise * time
        # Можно было написать вот так:
        # xt = noise + true_velocity * (1 - time)

        pred_velocity = model(xt, time)  # передаём в модель сэмплы и time
		
		# ошибка между ожидаемым и предсказанным значением
        loss = torch.mean((true_velocity - pred_velocity) ** 2)  
        epoch_loss += loss.item()  # накапливаем ошибку для логирования

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    if epoch % 50 == 0:  # Каждые 50 эпох отчитываемся о прогрессе
        print(f"Epoch {epoch + 1} completed.")
        print(f"Loss: {epoch_loss / len(subset) * 1000:.2f}")
        
# По окончании тренировки сохраняем модель в файл
safetensors.torch.save_model(model, "./mnist_model_1.sft")

И ещё раз напомню, что тут вообще происходит: Каждую итерацию цикла мы извлекаем из датасета набор (батч) 256 чёрно-белых изображений (сэмплов) размером 28 на 28 пикселей. Этот батч представляет собой тензор с шейпом (256, 1, 28, 28). Будь изображения цветные, то тензор был бы (256, 3, 28, 28). Чтобы натренировать модель нам нужны сэмплы с разной степенью “зашумлённости”. Как нам их получить? Нужно создать тензор с шумом, при этом такого же размера, что и батч изображений, а потом просто линейно интерполировать между этими двумя тензорами. Вот только чтобы линейно интерполировать между двумя тензорами и получить новый (зашумлённый) тензор нам нужен какой-то коэффициент. То есть, коэффициент 0.5 означает что, полученный тензор будет ровно на полпути между изображением и шумом, а коэффициент 0.1 – шумным только на 10%. Легче это визуально показать:

Большая гифка про добавление шума

Тренировочный цикл практически 1 в 1 то, что было в предыдущей статье. Пока проигнорируем тот факт, что model мы до сих пор не создали, посмотрим вот на эту строку:

xt = x * (1 - time) + noise * time

Тут мы хотим получить частично зашумлённые сэмплы линейно интерполируя между целевыми сэмплами и шумом используя time в качестве коэффициента. Всё хорошо, вот только этот код упадёт с ошибкой ^[3]. Чтобы понять в чём дело, распишем какой шейп имеют все 3 тензора:

x0     (256, 1, 28, 28)
noise  (256, 1, 28, 28)
time   (256, 1)

При попытке умножить noise на time PyTorch выдаст нам такую ошибку:

RuntimeError: The size of tensor a (64) must match the size of tensor b (28) at non-singleton dimension 2

А оно и понятно, вот просто подумайте, мы хотим умножить набор из 200704 (256 x 1 x 28 x 28) чисел на другой набор уже из 256 (256 x 1) чисел, чтобы в итоге получить ещё одни набор из 200704 чисел. И как, спрашивается, PyTorch должен это сделать? Так-то мы хотим умножить каждое число из тензора noise на соответствующее ему из тензора time. У нас бы всё получилось если бы тензор time имел такую же форму (шейп) как и тензор noise (256, 1, 28, 28). И мы можем этого достичь, нужно просто размножить (расширить) тензор:

(256, 1) -> (256, 1, 28, 28)

Всего-то и делов – добавить 2 дополнительных измерения, а потом скопировать единственное число пока не получится матрица 28×28. При чём добавлять измерений мы можем тензору сколько угодно – количество элементов в нём не изменится. То есть тензор с шейпом (256, 1) содержит столько же элементов сколько и тензор с шейпом (256, 1, 1, 1). Для этого как раз подходит метод reshape:

ext_time = time.reshape(time.size(0), 1, 1, 1)  # будет (256, 1, 1, 1)

Осталось только скопи…. А не надо ничего копировать больше! PyTorch вполне способен превратить тензор (256, 1, 1, 1) в тензор (256, 1, 28, 28) ориентируясь на размер второго тензора в операции умножения. Загляните в документацию по broadcasting ^[4], если хотите подробностей.

И, кстати, небольшое пояснение к time.size(0) – можно было бы просто написать BATCH_SIZE, вот только проблема в том, что когда мы итерируемся по датасету и извлекаем из него один батч за другим в самой последней итерации может оказаться меньше элементов чем BATCH_SIZE.
Поясню этот момент. Представьте, что у нас есть вот такой список:

[1, 2, 3, 6, 5, 7, 3, 2]

И мы решаем проитерировать его по 3 элемента за раз:

[1, 2, 3]
[6, 5, 7]
[3, 2]

Как видите последний “батч” вышел короче чем другие. Надеюсь стало понятнее.

Возвращаемся к коду. Заменяем вот эту строку:

xt = x0 * (1 - time) + noise * time

на

ext_time = time.reshape(time.size(0), 1, 1, 1)
xt = x0 * (1 - ext_time) + noise * ext_time

Ладно, с этим разобрались, приступаем к самой модели

Собираем модель

В качестве отправной точки возьмём модель из предыдущей статьи:

class DenoiserBlock(nn.Module):  
    def __init__(self, hidden_dim, mlp_ratio):  
        super().__init__()  
        self.ln = nn.LayerNorm(hidden_dim)  
        self.mlp = nn.Sequential(  
            nn.Linear(hidden_dim, hidden_dim * mlp_ratio),  
            nn.SiLU(),  
            nn.Linear(hidden_dim * mlp_ratio, hidden_dim),  
        )  
  
    def forward(self, x):  
        z = self.ln(x)
        z = self.mlp(z)
        return z  
  
  
class Denoiser(nn.Module):  
    def __init__(self, hidden_dims, num_blocks):  
        super().__init__()  
        self.input_encoder = nn.Linear(2, hidden_dims)  
        block_list = [DenoiserBlock(hidden_dims, 4) for _ in range(num_blocks)]  
        self.blocks = nn.ModuleList(block_list)  
        self.output_decoder = nn.Linear(hidden_dims, 2)  
        self.time_linear = nn.Sequential(  
            nn.Linear(1, hidden_dims),  
            nn.LayerNorm(hidden_dims)
        )  
  
    def forward(self, x, t):  
        hidden = self.input_encoder(x)  # (B, 2) -> (B, 16)  
        time_embedding = self.time_linear(t)
        for block in self.blocks:  
	        hidden = hidden + block(hidden + time_embedding)  
        return self.output_decoder(hidden)  # (B, 16) -> (B, 2)

Сейчас она принимает 2 параметра – тензор точек с шейпом (B, 2) и тензор времени (шаг, timestep) с шейпом (B, 1). Нам надо работать не с точками на плоскости, а с изображениями, поэтому первым параметром наша модель должна принимать 4D тензор с шейпом (B, 1, 28, 28). B – это размер батча, если кто забыл, 256 в нашем случае.

Тут очень удобно получается, что в нашей модели уже есть слой input_encoder, который трансформирует входной тензор во внутреннее представление, и output_decoder, который проделывает обратную операцию. Так что всего лишь остаётся модифицировать эти слои, чтобы они работали с новыми входными данными:
Вот это

self.input_encoder = nn.Linear(2, hidden_dims)

Заменяем на

self.input_encoder = nn.Sequential(
	nn.Flatten(start_dim=1),  # (B, 1, 28, 28) -> (B, 784)
	nn.Linear(28*28, hidden_dims),
)

nn.Flatter – это просто операция слияния измерений в тензоре. Тренируемых параметров не содержит, в отличие уже знакомого нам nn.Linear.

Теперь с output decoder. Превращаем

self.output_decoder = nn.Linear(hidden_dims, 2)

В такое:

self.output_decoder = nn.Sequential(
	nn.Linear(hidden_dims, hidden_dims * 2),
	nn.SiLU(),
	nn.Linear(hidden_dims * 2, SIZE * SIZE),
	nn.Unflatten(1, (1, SIZE, SIZE)),  # (B, 784) -> (B, 1, SIZE, SIZE)
)

А ещё уберём time_embedding для чистоты эксперимента:

def forward(self, x, t):  
        hidden = self.input_encoder(x)
        time_embedding = self.time_linear(t)  # пока игнорируем
        for block in self.blocks:  
	        hidden = hidden + block(hidden)  
        return self.output_decoder(hidden)

Пока что наша новая модель не сильно отличается от предыдущей – всего-то адаптировали энкодер и декодер под новый формат. Пока что.

Ладно, давайте инициализировать модель и попробуем её натренировать

BATCH_SIZE = 256
LR = 6e-4
DEVICE = 'cuda'
EPOCHS = 600

subset = Subset(dataset, torch.randperm(4096 * 2))
data_loader = torch.utils.data.DataLoader(
    dataset=subset,
    batch_size=BATCH_SIZE,
    shuffle=True,
)
model = Denoiser(hidden_dims=600, num_blocks=2)  # вектор из 600 элементов
model.to(DEVICE)  # всё должно быть на одном девайсе
optimizer = torch.optim.AdamW(model.parameters(), lr=LR)

И получаем в итоге:

Как думаете, что пошло не так? Слишком большой датасет? Неудачная архитектура? Модель недостаточно глубокая? Я расскажу в чём дело, но давайте сначала разберёмся откуда вообще взялась эта картинка.

Понимаете, во время тренировки генеративной модели полезно не только следить за уменьшением показателя loss (ошибка), но и за тем какие изображения (сэмплы) модель способна генерить. Поэтому в моё коде тренировки логируется не только loss, но и генерируются и сохраняются сэмплы чтобы наглядно наблюдать как модель учится генерить изображения. Вот так это выглядит:

if epoch % ((EPOCHS - 1) // num_samples) == 0:
	with torch.no_grad():
		log_sample(sample_noise, model)  # генерим прямо походу обучения
if epoch % 50 == 0:  # Каждые 50 эпох отчитываемся о прогрессе
        print(f"Epoch {epoch + 1} completed.")
        print(f"Loss: {epoch_loss / len(subset) * 1000:.2f}")

Не буду здесь углубляться в то, что делает функция log_sample – всё равно можно посмотреть в финальном коде. Просто генерим 5 сэмплов несколько раз за время обучения ^[5] и сохраняем их все в виде одного изображения – чтобы потом видеть “прогресс” в обучении. По рисунку выше видно, что модель уже после первых 20% времени обучения научилась генерить из шума бесформенных кляксы и на этом остановилась. А причина в том, что данные не нормализованы.

Я, конечно, мог бы поступить лениво и просто сказать, что нужно добавить T.Normalize((0.175,), (0.35,))
в конец списка трансформаторов:

transforms = T.Compose([
    T.RandomRotation(degrees=(-90, -90)),
    T.RandomHorizontalFlip(p=1),
    T.ToTensor(),
    T.Normalize((0.175,), (0.35,)),  # Вот так
])

Но я так не поступлю. Держите объяснение:

Давайте вспомним, что входной датасет у нас это одноканальные PIL-изображения, которые представляют собой набор пикселей каждый в интервале от 0 (черные) до 255 (белые). Наш трансформатор ToTensor() помимо всего прочего ещё и “сжимает” входное изображение в интервал от 0 (черные) до 1 (белые). А теперь припоминаем как мы создаём “зашумлённые” изображения во время тренировки – интерполируем между шумом и “чистыми” изображениями. Вот только чистые изображения у нас находятся в интервале [0, 1] а шум где-то в интервале [-2, 2] (да, я в курсе ) – получается что когда мы создаём наполовину зашумлённые изображения, то шум просто “скрывает” данные. По другому можно сказать, что 95% процентов времени обучения модель не видит данные в шуме – не может их различить и из-за этого не может нормально обучиться. Что же в таком случае сделает Normalize?

На самом деле всё просто – первое число (0.175) – это то что мы отнимем от каждого “пикселя” во входном изображении. Нужно это для того, чтобы средняя стала равняться 0. А откуда вообще взялось число 0.175? Да я просто посчитал среднее значения для всех пикселей в нашем датасете. Большинство пикселей равнялось 0 – чёрный фон ведь, поэтому вычисленное среднее смещено к 0. Значит, отняли среднее и теперь новое среднее значение это 0. Осталось лишь разделить 0.35. Может уже догадались, что 0.35 – это стандартное отклонение нашего датасета. Разделив все данные на это число мы получим новый набор данных, но теперь уже со средним 0 и стандартным отклонением 1.0 – как раз совпадающий со средним и стандартным отклонением гауссового шума, из которого мы берём наши “шумные” сэмплы. Таким образом, мы добились того, что и шум и чистые данные статистически равнозначны и обучение модели должно пройти лучше.

Запускаем тренировку и получаем:

Будем считать это нашей точкой отсчёта и начнём улучшать архитектуру нашей модели.

Версия 0 (downsample)

Добавляю нулевую версию, уже после того как почти дописал статью. В общем, тут такое дело: двухслойная модель шириной 600 скрытых параметров не потянула моделирование датасета изображений, каждое из которых 784 пикселей. Поэтому, признав поражение, приходится уменьшить разрешение целевых изображений. Будут 24×24 пикселя.

SIZE = 24
transforms = T.Compose([
    T.RandomRotation(degrees=(-90, -90)),
    T.RandomHorizontalFlip(p=1),
    T.Resize(SIZE),  # Как уменьшить фотку в фотошопе
    T.ToTensor(),
    T.Normalize((0.175,), (0.35,)),  # Вот так
])

Заменяем во всём коде 28 на SIZEи запускаем тренировку

Вот от этого теперь будем отталкиваться

Версия 1 (timestep condition)

Прежде всего, давайте вернём информацию о временном шаге (timestep), чтобы модели легче было распознавать на какой стадии “зашумления” находятся обучающие сэмплы.

Было:

    def forward(self, x, t):
        hidden = self.input_encoder(x)
        #  time_embedding = self.time_linear(t)
        #  hidden = hidden + time_embedding
        for block in self.blocks:
            hidden = hidden + block(hidden)
        return self.output_decoder(hidden)

Стало:

    def forward(self, x, t):
        hidden = self.input_encoder(x)
        time_embedding = self.time_linear(t)
        hidden = hidden + time_embedding  # информация о времени добавилась
        for block in self.blocks:
            hidden = hidden + block(hidden)
        return self.output_decoder(hidden)

Небольшая разница проглядывается

Есть способ улучшить результат. Для этого нужно поменять то, как модель использует информацию.

Версия 2 (modulation)

Давайте сначала разберёмся с определениями. Вот какую информацию мы передаём модели, когда хотим что-то сгенерировать? Можно передать просто сэмлпы разной степени зашумлённости и тогда модель должна каким-то образом только только из этой информации определить степень зашумления и предсказать нужный вектор. Но ведь можно упростить модели задачу – передать ей на вход не только шумные сэмплы, но ещё и дополнительную подсказку (условие), которая “расскажет” модели сколько шума содержится в переданном сэмпле. Можно по другому сказать: на какой точки траектории находится находится сэмпл, он ближе к целевому распределению или к сэмплам гауссового шума. Эта дополнительная информация позволит модели легче произвести обобщение, а это, в общем-то, и есть цель обучения. С практической точки зрения ^[6] тут понятно – если дать модели дополнительную информацию на вход, то результат будет лучше. Наглядно будет видно, когда мы дойдём до генерации по классам – качество генерации резко возрастёт. А пока надо запомнить, что когда мы передаём модели дополнительную информацию (помимо самого шумного сэмпла), то это называется условная генерация. А если подобной информации нет, то это безусловная генерация.

Сейчас в версии 1 единственное условие, которое мы передаём в модель – это время

def forward(self, x, t):  # t - это time
	hidden = self.input_encoder(x)
	time_embedding = self.time_linear(t)  # делаем тензор-условие
	hidden = hidden + time_embedding  # и просто прибавляем к данным

Сложение тензоров – это вполне себе рабочий способ добавить дополнительную информацию, но в случае диффузных моделей малоэффективный. Но как ещё мы можем повлиять на генерацию? Ответ мы найдём в публикации по диффузным трансформерам:

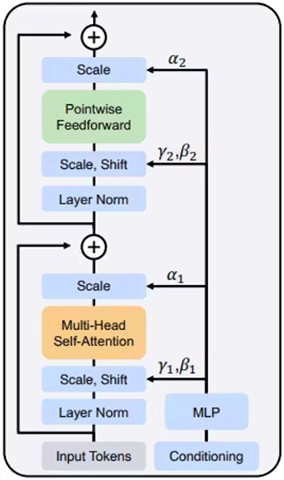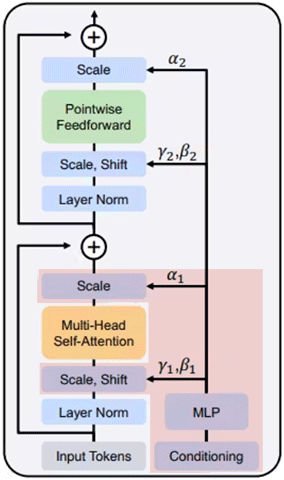
На этой диаграмме подсвечен механизм управления генерацией через манипуляцию Scale и Shift. На самом деле, всё просто. Вот есть у нас (допустим) скрытое представление – одномерный тензор (вектор) вот с таким значениями:

[0, 1.2, 0.3, -0.9]

И два вот таких вектора Scale и Shift:

[1.1, 0.9, -1, -0.8] – это Scale

[0.1, 0.2, -0.07, 0] – а это Shift

Как эти 2 вектора повлияют на вектор скрытого представления?
А вот так:
[0, 1.2, 0.3, -0.9]
x
[1.1, 0.9, -1, -0.8]
=
[0, 1.08, -3, 0.72] – это после операции scale

И потом:
[0, 1.08, -3, 0.72]
+
[0.1, 0.2, -0.07, 0]
=
[0.1, 1.28, -3.07, 0.72] – это после операции shift

В коде это будет выглядеть вот так:

z = z * scale + shift  # z - это переменная скрытого представления

Выглядит как непонятно откуда взявшаяся операция, но вспомните, что мы моделируем – мы моделируем трансформацию исходного распределения в целевое. Скрытое представление, с которым мы проделываем все эти операции – это лишь одна “точка” из распределения. Умножая и прибавляя некие значения к каждой точке распределения приводит к тому, что распределение как бы сжимается или растягивается (умножение) и сдвигается в некотором направлении (сложение). И всё это происходит в некоем многомерном пространстве – в случае нашей модели пространство 600-мерное.

Но вы спросите – откуда вообще берутся эти вектора Scale и Shift? Видите на диаграмме блок “MLP” справа внизу – он на вход получает вектор-условие, а на выходе у него вектор размера в три раза больше чем размер скрытого представления. Это для того, чтобы потом этот длинный вектор разделить на 3 части – Scale, Shift и Gate. Вот иллюстрация:

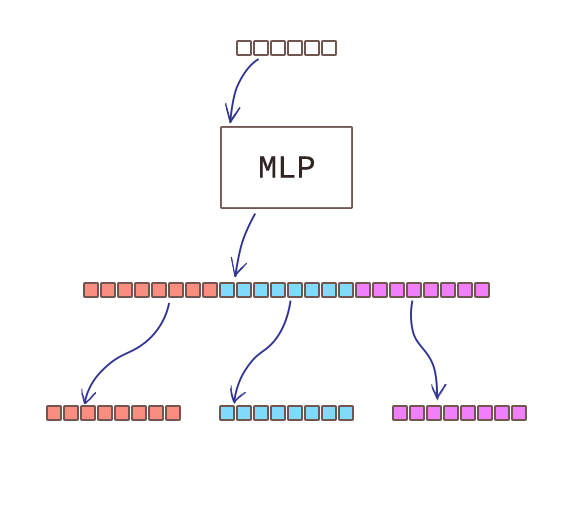
Наш 32-размерный вектор с условием проходит через MLP и трансформируется в 600 * 3 = 1800 размерный вектор. 600 – это размерность скрытого представления в нашей модели. Потом просто разделяем его на 3 равные части каждая размером в 600, которые становятся векторами Scale, Shift и Gate. Вам, наверное, хочется спросить, что это за Gate? На самом деле, но работает также как Scale (умножается на скрытое преставление), но служит немного для другой цели. Дочитайте до конца секции и поймёте.

Теперь воплотим это в коде:

    def __init__(self, hidden_dim, mlp_ratio, condition_dim):  # новый параметр
        super().__init__()
        self.ln = nn.LayerNorm(hidden_dim)
        self.mlp = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim * mlp_ratio),
            nn.SiLU(),
            nn.Linear(hidden_dim * mlp_ratio, hidden_dim),
        )
        self.modulator_mlp = nn.Sequential(  # MLP
            nn.Linear(condition_dim, condition_dim * 4),
            nn.SiLU(),
            nn.Linear(condition_dim * 4, hidden_dim * 3),
        )

	
    def forward(self, x, c):
	    # Вычисляем, разделяем на 3 куска и применяем
        scale, shift, gate = self.modulator_mlp(c).chunk(3, dim=1)
        z = self.ln(x)
        z = z * scale + shift  # после нормализации
        z = self.mlp(z)
        z = z * gate
        return z

self.modulator_mlp(c) вернёт нам тензор с шейпом (B, 1800), а вызов .chunk(3, dim=1) разделит его на 3 равные части: ((B, 600), (B, 600), (B, 600)), которые мы и будем использовать. Итак, подытожим: условная информация (время) – это вектор размером 32. Он проходит через дополнительную модель modulator_mlp, которая создаёт на его основе вектор размеров в три раз больше чем скрытое представление z. После этого мы рубим этот вектор на 3 части и используем их, чтобы “оказать влияние” на скрытое представление через умножение и складывание – операции, которые, по сути, трансформирует моделируемое распределение. Таким образом, каждый блок теперь “знает” условную информацию и имеет больше возможностей учесть эту дополнительную условную информацию в своей работе.

Ладно, думаю стало понятнее. Теперь, конечно, нужно дописать код – у нас ведь появился новый параметр в конструкторе блока: condition_dim, поэтому надо поправить размерность вектора, который выдаёт time_linear в основной модели:

Вместо

self.time_linear = nn.Sequential(  
    nn.Linear(1, hidden_dims),
    nn.LayerNorm(hidden_dims) 
)

Написать

self.time_linear = nn.Sequential(  
    nn.Linear(1, condition_dim),  
    nn.LayerNorm(condition_dim)  
)

condition_dim появится в конструкторе самой модели

def __init__(self, hidden_dims, num_blocks, condition_dim):

И теперь нужен при создании блоков:

block_list = [DenoiserBlock(hidden_dims, 4, condition_dim) for _ in range(num_blocks)]

Запускаем тренировку и видим, что результат особо не улучшился:

А дело вот в чём – изначально мы инициализируем modulator_mlp случайными весами, которые при добавлении к скрытому представлению оказывают дополнительную нагрузку на тренировку – сигнал становится слишком шумным. Но есть способ это поправить. Первый раз я узнал про него как раз в публикации про Diffuison Transformers – надо инициализировать веса modulator_mlp так, чтобы изначально выдаваемый её вектор был нулевым. Что значит нулевым? А то что и Scale, и Shift, и Gate будет содержать только 0, другими словами, получатся 3 вектора размером в 600 заполненные нулями. Но зачем нам векторы, заполненные нулями? Они дают нам возможность переписать метод forward у DenoiserBlock вот так:

def forward(self, x, c):
        scale, shift, gate = self.modulator_mlp(c).chunk(3, dim=1)
        z = self.ln(x)
        z = z * (1 - scale) + shift
        z = self.mlp(z)
        z = z * gate
        return z

Подумайте, что будет происходить если все элементы векторов scale, shift и gate равны 0? Возвращаемое значение (z) будет равняться нулевому вектору, все значения которого равны 0! А сейчас вспомните как мы используем результат работы блока в основной модели-денойзере:

hidden = hidden + block(hidden, time_embedding)

hidden + нулевой вектор == hidden. Другими словами, мы полностью обнулили работу блока. Главным образом из-за вот этого “умножения на 0”: z = z * gate. Вот для чего gate и нужен – сгладить сигнал для градиента. Главное тут понять, что “нулевым” вектора Scale, Shift и Gate будут только первую итерацию тренировки – после первого же вызова optimizer.step() градиент поменяет веса modulator_mlp и модель будет обучаться своим чередом. Но за счёт того, что изначально она инициализировалась нулями и не добавляла шум в сигнал, последующее обучение пройдёт более “гладко”. Сейчас мы в этом убедимся. В конец конструктора блока добавляем код инициализации весов:

self.modulator_mlp = nn.Sequential(  
    nn.Linear(cond_dims, cond_dims * 4),  
    nn.SiLU(),  
    nn.Linear(cond_dims * 4, hidden_dim * 3)  # вот этот слой
)
#  Linear делает x * weight + bias
nn.init.zeros_(self.modulator_mlp[-1].weight)  # все weight теперь 0
nn.init.zeros_(self.modulator_mlp[-1].bias)    # все bias теперь 0

теперь modulator_mlp стартует обучение с нулевым вектором на выходе. Всё остальное не меняется. Запускаем тренировку и…

Версия 3 (class condition)

Вы ведь помните, что наш EMNIST датасет содержит не просто сэмплы-изображения, но ещё и их классы (лейблы). Вот тут видно как класс картинки clazz извлекается из data_loader вместе с самой картинкой x0:

for epoch in range(EPOCHS):
    epoch_loss = 0
    for x0, clazz in data_loader:

clazz здесь – это просто индекс класса – всего 47, от 0 до 46. А откуда мы узнали, что их 47? Да просто создав переменную num_classes сразу после объявления датасета:

subset = Subset(dataset, torch.randperm(4096 * 2))  
num_classes = len(dataset.classes)

И что мы будем с этими классами делать? С помощью них мы обучим модель новому условию (классу изображения) – научим её генерировать не просто сэмплы, похожие на какие-то картинки из датасета EMNIS, а на конкретные символы – 1, 2, 8, b, c, k, w и прочие. Что ж, приступим.

Как и в случае с time_embedding нам нужно получить вектор, кодирующий условие класса (class_embedding), но на руках у нас опять лишь единственное целочисленное дискретное число. В случае с time мы создавали вектор-условие прогоняя time через time_linear, но индексы класса – это не интервал, поэтому мы будем действовать по-другому: создадим ассоциативный ^[7] массив (lookup table, мапа), где каждый индекс (класс) будет ассоциироваться с каким-то конкретным вектором. И как удачно получилось, что у Pytorch как раз есть для этого уже готовое решение: nn.Embedding. Добавляем его в начало конструктора Denoiser‘a:

def __init__(self, hidden_dims, num_blocks, condition_dim):  
    super().__init__()  
    self.class_embeddings = nn.Embedding(num_classes, condition_dim)

nn.Embedding создаёт набор векторов размером condition_dim в количестве num_classes, и даёт возможность к ним обращаться вот так:

self.class_embeddings(19)

Вектора инициализируются случайными значениями, но по ходу тренировки до них доходит градиент, поэтому они тоже будут обучаться.

Помимо class_embeddings нам понадобится ещё один MLP. Объявим его на следующей строке:

def __init__(self, hidden_dims, num_blocks, condition_dim):  
    super().__init__()  
    self.class_embeddings = nn.Embedding(num_classes, condition_dim)  
    self.class_mlp = nn.Sequential(  
        nn.Linear(condition_dim, condition_dim * 4),  
        nn.SiLU(),  
        nn.Linear(condition_dim * 4, condition_dim),  
    )

Осталось лишь обновить метод forward:

def forward(self, x, t, c):  # тепеть метод принимает индекс класса  
    hidden = self.input_encoder(x)
    time_embedding = self.time_linear(t)  
    class_embedding = self.class_embeddings(c)  # вытаскиваем эмбеддинг
    class_condition = self.class_mlp(class_embedding)  # прогоняем его через mlp
    # формируем объединённый вектор-условие
    # time_embedding можно было бы переименовать в time_condition
    condition = time_embedding + class_condition 
    for block in self.blocks:  
	    # отправляем объединённый вектор-условие в блок
        hidden = hidden + block(hidden, condition)
    return self.output_decoder(hidden)

Ну и код тренировки тоже подправить надо:

Вместо

pred_velocity = model(xt, time)  # передаём в модель сэмплы и time

Пишем

pred_velocity = model(xt, time, clazz)  # передаём в модель сэмплы, time и класс

Запускаем теперь тренировку и

Теперь символы (почти) отчётливо различимы, однако присутствует какая-то размытость. Пришлось потратить некоторое время, чтобы выяснить, что причина в излишне “жирном” output_decoder.

При удалении лишнего слоя из

self.output_decoder = nn.Sequential(
	nn.Linear(hidden_dims, hidden_dims * 2),
	nn.SiLU(),
	nn.Linear(hidden_dims * 2, SIZE * SIZE),
	nn.Unflatten(1, (1, SIZE, SIZE)),  # (B, 784) -> (B, 1, SIZE, SIZE)
)

Энкодер превращается в простое умножение на матрицу (плюс bias):

self.output_decoder = nn.Sequential(
	nn.Linear(hidden_dims, SIZE * SIZE),
	nn.Unflatten(1, (1, SIZE, SIZE)),  # (B, 784) -> (B, 1, SIZE, SIZE)
)

И финальный результат выглядит гораздо лучше:

Чем это можно объяснить? Странно это выглядит, когда при уменьшении размера модели она начинает выдавать сэмплы лучшего качества. Я вижу объяснение в том, что “жирный” output_decoder хоть и обладает потенциально лучшим качеством генерации, но при ограниченности “вычислительных ресурсов” – у нас тут всего 8192 * 600 = 4915200 итераций – слишком мощный output_decoder оттягивает часть этих ресурсов на себя и из-за этого понижает качество сэмплов. Чтобы выяснить действительно ли моя гипотеза верна придётся произвести небольшое исследование, так что пока догадка остаётся догадкой.

В результате получилась модель весом 27Mb, способная генерировать узнаваемые символы из датасета EMNIST. Цель выполнена! И финальный код доступен по ссылке ^[8].

Заключение

Что мы сделали по ходу статьи:

• Разобрались как работать с датасетом EMNIST

• Адаптировали код тренировки к 4D тензорам (изображения)

• Создали модель, способную генерировать чёрно-белые изображения

• Постепенно улучшали архитектуру модели, узнав как задавать условие генерации через модуляцию

На самом деле даже такую маленькую модель есть куда улучшать – использовать нелинейный шедулер, например – у нас уже на 60% зашумления изображения от шума не отличить.

Самое главное, что можно вынести из этой статьи – это не работа с датасетом и 4D-тензорами, а механизм управления генерацией через Scale, Shift и Gate – то что называют modulation. Именно это приближает нас конечной цели – к созданию Diffusion Transformer. Чем мы и займёмся в третьей (финальной) части – продолжение следует..!