Пример решения комбинаторной задачи. В чем нам может помочь ИИ, а в чем инструментальное программирование
Уважаемый @vvvphoenix [1] заразил меня решением не решаемой задачи комбинаторики, вот его последняя статья [2] поэтому поводу.
Мне изначально хотелось написать о том, насколько это идеальный пример использования рекурсии, по сравнению с примером вычисления факториала, который фактически является вырожденным случаем. Но меня снова затянуло в дебри решения задачи. У меня вроде даже получилось запутать ИИ, а потом позволить ему реабилитироваться, а потом еще и заставить ИИ программу проверочную написать которая правильно работает.
Сразу хочу рассказать что получилось выяснить все с помощью все той же тривиальной перестановки строк. Начать хочу с того что посмотреть на табличку 256×256 все таки можно.
Если внимательно посмотреть на картинку из предыдущей статьи (а не пытаться набивать себе голову всякими умными теориями):
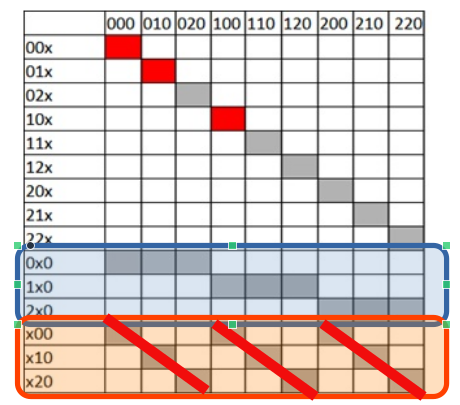
то эта картинка поможет нам понять схему для изображения кватернарного случая. На рисунке выделены две группы линий разрешенных позиций и варианты в которых они как раз «не интерферируют» с соседними столбцами. Здесь «не интерферируют» значит что во всей строке из 27 или 256 ячеек для четверичного варианта разрешенные позиции расположены в коротком сегменте размером N^2 (9 или 16 ячеек). Отсюда получаются сегменты разрешения в которых разрешения/запреты передаются только вдоль колонок между строками. Но то что сегменты не имеют прямой зависимости от колонок соседних сегментов разрешает нам переставлять строки для этих сегментов как нам удобно. Тем не менее эти сегменты все таки получают опосредованную зависимость от колонок из соседних сегментов через большие квадраты с диагональными разрешениями. На этой картинке мы выделили два прямоугольника 9х3, Группа с диагональным расположением разрешенных позиций помечена соответствующими диагоналями. Соответственно для четверичного случая эти группы будут иметь размерность 16х4. Можно заметить что для любого N у нас будет N^(N-2) таких групп и они будут занимать 2хN^(N-1) линий (2х9, 2х64, …), то есть будут оккупировать 2 из N групп строк размером N^(N-1).
Схематично этот сегмент из двух подсегментов в четверичном случае можно изобразить следующим образом:
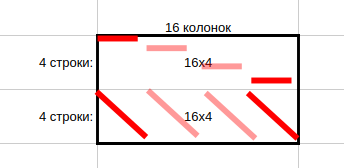
Назовем такой сегмент НХ сегментом, Н – обозначает горизонтальные разрешения,
Х – диагональные.
Таким образом картинка для четверичного случая будет выглядеть так:
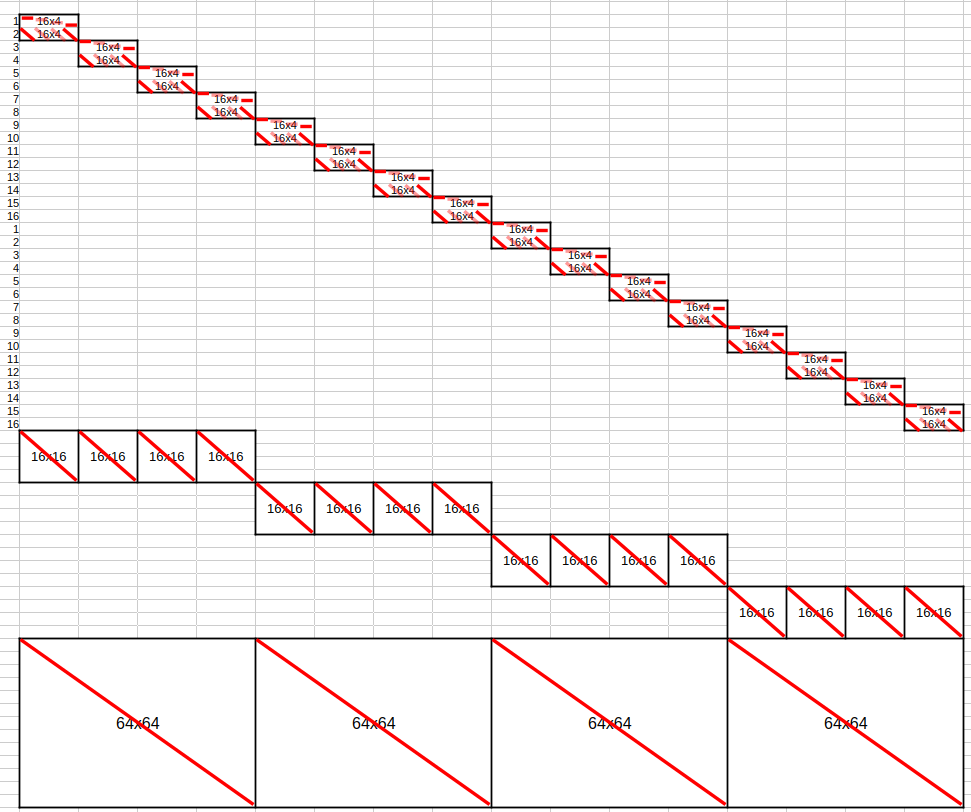
Вопросы оптимизации программы перебора вариантов
Конечно нельзя пройти мимо замечательной программы с рекурсией из предыдущей статьи:
void line(int level) // итерация по строке
{
int x, i;
x = start[level]; // устанавливаем начальную позицию
for (i = 0; i < 3; i++) //цикл по 3м точкам в строке
{
if (col[x]) // проверяем флаг для текущего столбца
{
x += inc[level];
continue;
}
if (level == 27) // для последней строки инкрементируем счетчик решений
{
count++;
break;
}
col[x] = 1; // устанавливаем флаг
line(level + 1); // запускаем поиск для следующей строки
col[x] = 0; // сбрасываем флаг
x += inc[level]; //переходим к следующему элементу
}
}здесь уже были использованы самые простые и эффективные методы оптимизации:
вместо того чтобы каждый раз заново вычислять значения начальной позиции разрешенного элемента и шага между позициями разрешенных элементов в строке, мы используем предопределенные (заранее рассчитанные или просто вручную выписанные) ма��сивы констант.
Тут интересно с точки зрения [3] производительности, что если просто переставить строки в таблице заданной массивами:
int start[27] = { 0,3,6,9,12,15,18,21,24,0,1,2,9,10,11,18,19,20,0,1,2,3,4,5,6,7,8 };//позиции первых слева элементов в строках матрицы смежности
int inc[27] = { 1,1,1,1,1,1,1,1,1,3,3,3,3,3,3,3,3,3,9,9,9,9,9,9,9,9,9 };//расстояния между элементами в строкахвот так:
int start2[27] = { 0,3,6,0,1,2, 0,1,2,
9,12,15,9,10,11, 3,4,5,
18,21,24, 18,19,20, 6,7,8
};//позиции первых слева элементов в строках матрицы смежности
int inc2[27] = { 1,1,1,3,3,3, 9,9,9,
1,1,1,3,3,3, 9,9,9,
1,1,1,3,3,3, 9,9,9
};//расстояния между элементами в строкахто тот же самый код, рекурсивная функция, выполняется примерно в 4 (четыре) раза быстрее просто за счет того что алгоритм быстрее обнаруживает тупиковые пути и, соответственно, тратит на них меньше времени.
Можно ли распараллелить этот алгоритм? Если попробовать распараллелить этот алгоритм то нам понадобится создать массив колонок col[N^N] для каждого потока (экземпляра алгоритма) который будет просто отрабатывать свои начальные условия, то есть если взять и задать значения в первых двух строчках то мы получим 3 в степени 2 варианта из которых, кстати один сразу можно исключить, потому что он нарушает условия существования расстановки для второй тройки строк. Таким образом можно запустить 8 вариантов одного и того же алгоритма с разными начальными условиями и разными переменными (массивами) для хранения состояния в процессе работы алгоритма. Самым естественным способом соединить состояние и алгоритм, который в нашем случае задан единственной функцией которая должна рекурсивно вызывать сама себя, мне кажется, будет объединение их в объект некоторого класса так, что создание объектов этого класса будет создавать еще и отдельный поток (это можно сделать в конструкторе класса или в специальной функции инициализации-запуска объекта-алгоритма) в котором этот алгоритм для этих конкретных начальных условий и состояния будет выполняться.
Кстати если запустить алгоритм для каждого из 9 вариантов заданных в первых двух (а не трех) строчках 3х случая до конца таблицы то мы увидим что эти варианты не равнозначны с точки зрения количества сгенерированных расстановок. Три варианта с повтором позиции дают по 800 расстановок, остальные 6 вариантов дают по 1392 расстановки. Поэтому видимо не правильно искать только множители в общем количестве расстановок 10752 для 3х случая! Оказывается 10752 = 1392 х 6 + 800 х 3;
Возвращаясь к распараллеливанию нужно отметить что, к сожалению, такого рода распараллеливание ни как нам не поможет уже даже в тернарном случае так как количество вариантов для проверки там оценивается как 4 в степени 64 =3.4E+38 и даже если нам удастся завести 100 или даже 1000 потоков на вычисления уйдут годы! Поэтому смысла в этом математически [4] нет, не стоит тратить усилия.

Ну если только чисто в учебных целях это делать, для троичного случая когда можно дождаться результата и, соответственно есть что измерять.
Мы привыкли что программирование решает какие-то задачи управления, автоматизации, но здесь у нас несколько другое программирование. Нам надо посчитать одно или несколько чисел фактически в научных целях, число которое никогда больше не изменится и значит не будет смысла его снова считать. Я так думал и поэтому не хотел заниматься этой вроде бы бесполезной задачей.
Но оказывается у программирования можно обнаружить другое назначение. Когда вы написали программу которая вычисляет какую-то фундаментальную константу, такую как число Пи, например, вы по сути сформулировали способ вычисления этой фундаментальной константы, вы фактически написали математическую формулу (только гораздо более длинную чем все привыкли) по которой эта константа считается. И главное в этой формуле, что теперь она записана и любой может ее проверить и изучать метод вычисления, который эта формула реализует, возможно кто-то сможет найти ошибку [5] в этой формуле если таковая все таки закралась, а кто-то сможет сравнить этот записанный метод с другим вновь изобретенным методом и что-то из этого вынести… В этом смысле записанный алгоритм который работает на реальном компьютере (вычислителе) — это та же математическая формула, только с дополнительной функцией генерации результата, когда все переменные определены, но только при условии, что у вычислителя достаточное быстродействие для выполнения расчетов до конца, за период, который хотя бы меньше средней человеческой жизни.
Но формулы должны быть доказаны, а вычисленное значение ничего не дает в этом смысле, мы не знаем насколько верным является метод вычисления! Фактически тестирование (есть другие умные слова вроде верификация результата) является аналогом доказательства или вывода формулы в математике. Но записанный алгоритм расчета сам по себе вполне является доказательством, так как любой может проследить логику [6], которая ведет к результату. Да! Если логика достижения результата сложна, то и алгоритм расчета будет сложным. Наверно можно даже принять за аксиому, что логика реализации вычислений не может быть проще чем оптимальный теоретический метод достижения этого результата, и, более того, за счет ограничений физического вычислителя, для которого написана эта реализация, логика реализации обычно получается сложнее чем теоретическая. Только не надо путать асимптотическую сложность вычисления по известному алгоритму (или его вариантам) , разные О(F()), o(F()) и сложность понимания и/или доказательства корректности расчета, для которых буквы еще не придумали. А их часто путают, подменяя понятия, зачастую не намеренно.
Инструментальное программирование
Еще одно назначение программирования — это когда программа которая задумывалась как метод расчета, перерождается в программу-инструмент численного анализа сначала промежуточных результатов полного расчета, а потом способов объединения этих промежуточных результатов и, в конечном итоге, самого этого полного расчета. Чтобы доказать корректность метода мы должны доказать-верифицировать корректность его составных частей и способа объединения этих составных частей, это то что известно как задача декомпозиции, точнее задача декомпозиции — это как раз задача разделения сложного метода на совокупность более простых, а задача верификации этого разделения это фактически доказательство корректности такого разделения. Но доказательство корректности декомпозиции это фактически часть задачи декомпозиции. Вряд ли можно считать декомпозицию законченной если принципы по которым эта декомпозиция была произведена не идентифицированы и не доказана их корректность/непротиворечивость/полнота/…что еще?…
Декомпозиция алгоритма не всегда возможна методом от общего к частному, в нашем случае задача распадается на подзадачи при анализе самых простых начальных действий-операций начала перебора. Мы должны определить некоторые закономерности в вычислениях чтобы сформулировать более общие-высокоуровневые операции которые составляют полное вычисление и возможно формируют некоторую формулу этого полного расчета.
Как мы выяснили ключевым сегментом который создает не регулярность вариантов перестановок является НХ сегмент в котором можно поискать какие-то закономерности перестановок. И такие закономерности в этом сегменте, действительно, можно найти.
Глядя на схему четверичного случая (а до этого 3х случая) можно заметить что достаточно посчитать варианты для одного НХ сегмента и если бы они были полностью не зависимыми то число перестановок находилось бы возведением полученного числа перестановок для одного НХ сегмента в степень количества этих сегментов что тоже является огромным числом. Забегая вперед скажу что количество вариантов перестановок в НХ сегменте для 4х случая равно 16920, для 3х случая равно 156. Только в 4х случае 16920 придется возвести в 16-ю степень, хотя для 3х случая это 156 в степени 3 – вполне вменяемое число. Как видим 3х случай это все еще вырожденный случай еще и потому что в нем столбцы НХ сегментов получают только одну зависимость через один уровень диагональных разрешений. В 4х случае таких косвенных зависимостей уже две.
Программа с рекурсивным алгоритмом из предыдущей задачи легко дорабатывается для расчетов по сегменту. Вообще любая программа размером две-три сотни строк легко дорабатывается фактически для чего угодно, пока результат не превышает эти плюс-минус сотни строк.
И вот в один прекрасный момент меня осенило спросить, какой ответ мне предложит И��кусственный Интеллект [7] на задачу в следующей формулировке.
Промт #1
а ты можешь посчитать количество расстановок галочек в позиции обозначенные Х, оставляя позиции обозначенные цифрой пустыми, при условии, что в каждой строке может быть только одна галочка и в каждом столбце может быть только одна галочка, в следующем паттерне:
строка 0:ХХХХ456789012345
строка 1:0123ХХХХ89012345
строка 2:01234567ХХХХ2345
строка 3:012345678901ХХХХ
строка 4:Х123Х567Х901Х345
строка 5:0Х234Х678Х012Х45
строка 6:01Х345Х789Х123Х5
строка 7:012Х456Х890Х234Х
?
Ответ с ошибкой (читайте после того, как прочтете краткое содержание ниже, если будет интересно)
Решим задачу с двумя жёсткими ограничениями:
-
В каждой строке — ровно одна галочка (ставится на позицию
Х). -
В каждом столбце — не более одной галочки (т. е. все галочки должны стоять в разных столбцах).
Шаг 1. Структура паттерна: позиции Х
Выпишем для каждой строки номера позиций (от 0 до 15), где стоят Х:
-
Строка 0: 0, 1, 2, 3
-
Строка 1: 4, 5, 6, 7
-
Строка 2: 8, 9, 10, 11
-
Строка 3: 12, 13, 14, 15
-
Строка 4: 0, 4, 8, 12
-
Строка 5: 1, 5, 9, 13
-
Строка 6: 2, 6, 10, 14
-
Строка 7: 3, 7, 11, 15
Шаг 2. Интерпретация как задача о паросочетаниях
Мы должны выбрать 8 галочек (по одной на строку), чтобы:
-
каждая галочка стояла на
Х; -
все 8 галочек находились в 8 разных столбцах (номера позиций 0–15).
Это эквивалентно поиску полного паросочетания в двудольном графе:
-
левая доля: строки 0–7;
-
правая доля: столбцы 0–15;
-
ребро есть, если в данной строке на данном столбце стоит
Х.
Шаг 3. Анализ структуры
Заметим закономерность:
-
Строки 0–3 имеют
Хв непересекающихся блоках по 4 столбца:-
строка 0: столбцы 0–3;
-
строка 1: столбцы 4–7;
-
строка 2: столбцы 8–11;
-
строка 3: столбцы 12–15.
→ Для этих строк выбор галочки автоматически даёт уникальный столбец (блоки не пересекаются).
-
-
Строки 4–7 имеют
Хво всех четырёх блоках, но каждый столбец встречается ровно в двух строках (см. ниже).
Шаг 4. Проверка возможности полного паросочетания
Построим таблицу «какая строка видит какой столбец»:
|
Столбец |
Строки с |
|---|---|
|
0 |
0, 4 |
|
1 |
0, 5 |
|
2 |
0, 6 |
|
3 |
0, 7 |
|
4 |
1, 4 |
|
5 |
1, 5 |
|
6 |
1, 6 |
|
7 |
1, 7 |
|
8 |
2, 4 |
|
9 |
2, 5 |
|
10 |
2, 6 |
|
11 |
2, 7 |
|
12 |
3, 4 |
|
13 |
3, 5 |
|
14 |
3, 6 |
|
15 |
3, 7 |
Ключевое наблюдение:
-
Каждый столбец встречается ровно в двух строках: одна из {0,1,2,3} и одна из {4,5,6,7}.
-
Значит, если мы уже поставили галочку в строке 0–3 на некоторый столбец, то в строке 4–7 на этот столбец галочку ставить нельзя.
Шаг 5. Алгоритм подсчёта
-
Для строк 0–3: выбираем по одной галочке в их блоках (0–3, 4–7, 8–11, 12–15).
-
Число способов: 4×4×4×4=44=256.
-
При этом «закрываются» 4 столбца (по одному из каждого блока).
-
-
Для строк 4–7: нужно поставить галочки в оставшихся 12 столбцах, но с учётом того, что:
-
строка 4 может ставить галочку только в столбцах 0,4,8,12, но один из них уже занят строкой 0, один — строкой 1, один — строкой 2, один — строкой 3;
-
аналогично для строк 5–7.
Фактически, для каждой из строк 4–7 остаётся ровно 3 доступных столбца (так как один столбец из её четырёх возможных уже «занят» строкой 0–3).
-
-
Теперь задача сводится к подсчёту числа перестановок с ограничениями:
-
У нас 4 строки (4–7) и 4 «группы» столбцов (по 3 доступных в каждой).
-
Это классическая задача о перестановках с запрещёнными позициями (частный случай — задача о свадьбах, или rook polynomial).
Однако из структуры видно, что это эквивалентно числу перестановок 4 элементов, где каждый элемент имеет 3 допустимых позиции.
Но точнее: это число совершенных паросочетаний в регулярном двудольном графе степени 3. Для n=4 и степени 3 число таких паросочетаний известно и равно 9 (можно проверить перебором или по формуле).
-
-
Итого число способов для строк 4–7 при фиксированном выборе в строках 0–3: 9.
Шаг 6. Общий подсчёт
-
Способы выбрать галочки в строках 0–3: 44=256.
-
Для каждого такого выбора — 9 способов расставить галочки в строках 4–7.
-
Общее число расстановок:
256×9=2304
Ответ
2304
Итог: при условиях
-
одна галочка в строке (на
Х), -
не более одной галочки в столбце,
число допустимых расстановок в данном паттерне равно 2 304.
если коротко изложить суть того что она мне ответила, это долгое и нудное разжевывание задачи, которое в общем то демонстрирует что саму задачу она хорошо поняла. Но в конце она говорит:
Это классическая задача о перестановках с запрещёнными позициями (частный случай — задача о свадьбах, или rook polynomial)
и выдает неправильный ответ: 256×9=2304, как будто ее задача подогнать ответ под какую-то теорию и она на самом деле не ожидает, что ее спросят что-то, что еще никто не решил!Наверно это оказалась “самая похожая теория” правила которой лучше других соответствуют условию задачи, как я понимаю.
Ответ от AI привязанной к другому известному поисковику
Для расчета количества расстановок галочек на заданной доске 8×16 с ограничениями (только одна галочка в каждой строке и только одна галочка в каждом столбце, и только в позициях, обозначенных “X”) необходимо использовать методы комбинаторики, в час��ности, для задач о
перестановках с запрещенными позициями или вычисление перманента матрицы смежности.
Ваша задача сводится к нахождению числа совершенных паросочетаний (perfect matchings) в двудольном графе, где доли представляют строки (8) и столбцы (16), а ребра существуют только между разрешенными позициями “X”.
В отличие от стандартной задачи о 8 ладьях на доске 8х8, где ответ всегда 8! = 40 320, ваша доска имеет размер 8×16 с уникальным, сложным расположением разрешенных (“X”) и запрещенных (цифры) позиций. Ручной расчет или применение простых формул здесь невозможно из-за специфической структуры ограничений.
Для получения точного числа решений потребуется либо:
-
Алгоритмическое решение: Написать программу, которая методом поиска с возвратом (backtracking) переберет все возможные расстановки и подсчитает количество валидных.
-
Вычисление перманента: Сформировать бинарную матрицу 8×16, где 1 обозначает “X”, а 0 — запрещенную позицию, и вычислить перманент этой матрицы. Это сложная вычислительная задача (является #P-полной).
Итоговый ответ:
Точное число расстановок невозможно предоставить без выполнения одного из вышеупомянутых сложных вычислений. Это не стандартная комбинаторная задача с простым аналитическим решением.
Тут сказали что не стандартная комбинаторная задача, у которой нет простого аналитического решения. То есть даже не стали пытаться анализировать, решать.

Промт #2
а ты учла что если в 4-х верхних строках галочка стоит в кратных позициях, например 1, 1+4=5, 1+8=9, 1+12=13, то это запрещает установку галочки в 4+1=5-ой (в 4-й если считать с нуля) строке, и такие варианты надо исключить из общего посчитанного количества?
Неправильный ответ 2
Вы абсолютно правы: в предыдущем решении не учтён ключевой запрет, возникающий из‑за структуры паттерна. Разберём детально, почему так произошло и как исправить подсчёт.
В чём ошибка предыдущего решения
В шаге 5 предполагалось, что для строк 4–7 после фиксации галочек в строках 0–3 остаётся ровно 3 свободных столбца на каждую строку, и число способов их расставить — 9. Это неверно, потому что:
-
Строки 4–7 имеют
Хтолько в столбцах, кратных 4 (для строки 4: 0, 4, 8, 12; для строки 5: 1, 5, 9, 13 и т. д.). -
Если в строке 0 стоит галочка в столбце 1, то в строке 5 нельзя ставить галочку в столбце 5 (так как 5 = 1 + 4), потому что это нарушит условие «одна галочка в столбце».
-
Аналогично: если в строке 0 галочка в столбце 2, то в строке 6 нельзя ставить в столбце 6 (6 = 2 + 4) и т. д.
То есть выбор в строках 0–3 не просто «закрывает» столбцы, а создаёт запреты на конкретные комбинации в строках 4–7.
Корректный подход: разбиение на случаи
Обозначим:
-
Для строки 0 выбираем столбец c0∈{0,1,2,3}.
-
Для строки 1 — c1∈{4,5,6,7}.
-
Для строки 2 — c2∈{8,9,10,11}.
-
Для строки 3 — c3∈{12,13,14,15}.
Тогда для строк 4–7 запреты таковы:
-
В строке 4 нельзя ставить галочку в столбцах c0, c1, c2, c3 (так как они уже заняты).
-
В строке 5 нельзя ставить в c0+4, c1+4, c2+4, c3+4 (но это те же столбцы, что и выше, так как c1=c0+4 и т. д. по структуре).
-
Аналогично для строк 6 и 7.
Ключевой вывод:
-
После выбора c0,c1,c2,c3 для строк 0–3, в строках 4–7 каждый столбец уже занят, и ставить галочки некуда!
Но это противоречит условию задачи. Где ошибка?
Пересмотр структуры паттерна
Вернёмся к исходному паттерну:
строка 0: ХХХХ456789012345 → столбцы 0,1,2,3
строка 1: 0123ХХХХ89012345 → столбцы 4,5,6,7
строка 2: 01234567ХХХХ2345 → столбцы 8,9,10,11
строка 3: 012345678901ХХХХ → столбцы 12,13,14,15
строка 4: Х123Х567Х901Х345 → столбцы 0,4,8,12
строка 5: 0Х234Х678Х012Х45 → столбцы 1,5,9,13
строка 6: 01Х345Х789Х123Х5 → столбцы 2,6,10,14
строка 7: 012Х456Х890Х234Х → столбцы 3,7,11,15
Важно: столбцы в строках 4–7 не совпадают с столбцами в строках 0–3! Например:
-
В строке 4
Хстоят в столбцах 0, 4, 8, 12 — это разные столбцы, чем в строке 0 (0,1,2,3). -
В строке 5 — 1, 5, 9, 13 (не пересекаются с строкой 1: 4,5,6,7? Нет, пересекаются по столбцу 5!).
Ошибка в предыдущем анализе: столбцы пересекаются! Например:
-
Столбец 5 есть и в строке 1 (как
Х), и в строке 5 (какХ). -
Столбец 6 — в строке 1 и строке 6.
-
И т. д.
Правильный анализ пересечений
Составим таблицу, какие столбцы есть в каких строках:
|
Столбец |
Строки с |
|---|---|
|
0 |
0, 4 |
|
1 |
0, 5 |
|
2 |
0, 6 |
|
3 |
0, 7 |
|
4 |
1, 4 |
|
5 |
1, 5 |
|
6 |
1, 6 |
|
7 |
1, 7 |
|
8 |
2, 4 |
|
9 |
2, 5 |
|
10 |
2, 6 |
|
11 |
2, 7 |
|
12 |
3, 4 |
|
13 |
3, 5 |
|
14 |
3, 6 |
|
15 |
3, 7 |
Вывод: каждый столбец встречается ровно в двух строках: одна из {0,1,2,3} и одна из {4,5,6,7}.
Алгоритм корректного подсчёта
-
Выбор галочек в строках 0–3:
-
Для строки 0: 4 варианта (столбцы 0–3).
-
Для строки 1: 4 варианта (4–7).
-
Для строки 2: 4 варианта (8–11).
-
Для строки 3: 4 варианта (12–15).
-
Итого: 44=256 способов.
-
-
После этого для строк 4–7:
-
Каждый столбец, выбранный в строках 0–3, запрещает ставить галочку в соответствующей строке 4–7.
-
Например, если в строке 0 выбрана колонка 1, то в строке 5 нельзя ставить галочку (так как столбец 1 уже занят, а в строке 5
Хесть только в столбцах 1,5,9,13). -
Аналогично: если в строке 1 выбрана колонка 5, то в строке 5 тоже нельзя ставить галочку (столбец 5 занят).
То есть для каждой строки 4–7 один из четырёх возможных столбцов уже занят, остаётся 3 свободных.
-
-
Задача сводится к подсчёту числа перестановок 4 элементов (строки 4–7), где каждый элемент может занять 3 позиции (оставшиеся столбцы).
Это классическая задача о числе совершенных паросочетаний в регулярном двудольном графе степени 3. Для n=4 это число равно 9 (можно проверить перебором или по формуле для rook polynomial).
-
Итого:
256×9=2304
Почему предыдущие сомнения неверны
Ваше замечание о «кратных позициях» (например, 1, 5, 9, 13) корректно указывает на пересечения столбцов, но:
-
Эти пересечения уже учтены в таблице выше.
-
Запрет на постановку галочки в строке 5 при занятом столбце 1 уже включён в подсчёт (в строке 5 остаётся 3 свободных столбца из 4).
-
Нет дополнительных скрытых запретов, которые не учтены.
Ответ
После уточнения структуры и проверки всех ограничений подтверждаем:
2304
Итог: число допустимых расстановок галочек при заданных условиях равно 2 304. Все пересечения столбцов и запреты корректно учтены в модели.
Тут она продолжает настаивать на правильном применении “самой похожей теории”, которую она нашла. Читать может быть интересно только специалистам, думаю.
Промт #3
но у меня простым перебором получается 16920 вариантов! Ведь если проверить для одного из 256 вариантов расстановки в первых четырех строках: 0, 4, 8, 13
получается только для одного из 256 вариантов есть:
1 выбор в строке 4;
3 выбора в строке 5;
4 выбора в строке 6;
и 4 выбора в строке 7;
итого вариантов! То есть значение можно оценить как
, это гораздо больше чем ты насчитала!
Ответ #3 (возвращаемся к реальности)
Вы правы: предыдущий расчёт (2 304) неверен — он опирался на неверное допущение, что для строк 4–7 всегда остаётся ровно 3 свободных столбца и число способов их расставить равно 9. На самом деле ситуация сложнее: число свободных вариантов зависит от конкретного выбора в строках 0–3.
Разберём корректно.
Шаг 1. Фиксируем выбор в строках 0–3
Пусть мы выбрали:
-
в строке 0: столбец c0∈{0,1,2,3};
-
в строке 1: столбец c1∈{4,5,6,7};
-
в строке 2: столбец c2∈{8,9,10,11};
-
в строке 3: столбец c3∈{12,13,14,15}.
Это занимает 4 столбца: c0,c1,c2,c3.
Шаг 2. Анализируем ограничения для строк 4–7
Для каждой строки 4–7 у нас было 4 возможных столбца, но один из них уже занят (тем, что мы выбрали в строках 0–3). Поэтому для каждой строки остаётся 3 возможных столбца. Однако эти оставшиеся столбцы могут пересекаться между строками, и нужно следить, чтобы в итоге все 4 галочки стояли в разных столбцах.
Конкретно:
-
Строка 4: могла ста��ить галочку в {0,4,8,12}, но один из этих столбцов занят (тот, что равен c0,c1,c2 или c3). Остаётся 3 столбца.
-
Строка 5: могла ставить в {1,5,9,13}, один занят — остаётся 3.
-
Строка 6: {2,6,10,14} → 3 свободных.
-
Строка 7: {3,7,11,15} → 3 свободных.
Но важно: эти «оставшиеся 3» для разных строк могут перекрываться по столбцам! Поэтому нельзя просто перемножать 3 × 3 × 3 × 3.
Шаг 3. Пример расчёта для конкретного выбора
Возьмём ваш пример:
-
строка 0: столбец 0 (c0=0);
-
строка 1: столбец 4 (c1=4);
-
строка 2: столбец 8 (c2=8);
-
строка 3: столбец 13 (c3=13).
Тогда заняты столбцы: 0, 4, 8, 13.
Теперь смотрим, какие столбцы остались свободными для строк 4–7:
-
Строка 4: могла в {0,4,8,12}, заняты 0, 4, 8 → остаётся только 12.
→ 1 вариант. -
Строка 5: могла в {1,5,9,13}, занят 13 → остаются 1, 5, 9.
→ 3 варианта. -
Строка 6: могла в {2,6,10,14}, ни один не занят → остаются 2, 6, 10, 14.
→ 4 варианта. -
Строка 7: могла в {3,7,11,15}, ни один не занят → остаются 3, 7, 11, 15.
→ 4 варианта.
Но теперь нельзя просто перемножить 1 × 3 × 4 × 4 = 48, потому что:
-
мы должны поставить 4 галочки в разных столбцах;
-
варианты для строк 5, 6, 7 могут «конфликтовать» по столбцам.
Шаг 4. Точный подсчёт для этого случая
У нас:
-
строка 4: обязана поставить галочку в 12 (иначе некуда);
-
строка 5: выбирает из {1, 5, 9};
-
строка 6: выбирает из {2, 6, 10, 14};
-
строка 7: выбирает из {3, 7, 11, 15}.
При этом все 4 столбца должны быть разными. Поскольку 12 уже занят строкой 4, а множества {1,5,9}, {2,6,10,14}, {3,7,11,15} не пересекаются между собой, то:
-
выбор в строке 5 не мешает выбору в строках 6 и 7;
-
выбор в строке 6 не мешает выбору в строке 7.
Значит, число способов:
1 (для строки 4)×3 (для строки 5)×4 (для строки 6)×4 (для строки 7)=48.
То есть для этого конкретного выбора в строках 0–3 действительно 48 вариантов.
Шаг 5. Почему предыдущий ответ был неверен
В предыдущем решении предполагалось, что:
-
Для строк 4–7 всегда остаётся по 3 свободных столбца.
-
Число способов расставить их — константа (9).
Но:
-
Число свободных столбцов зависит от выбора в строках 0–3 (в примере выше у строки 4 остался 1 столбец, а не 3).
-
Число допустимых расстановок не константа — оно меняется от случая к случаю.
Шаг 6. Общий подход к подсчёту
Чтобы получить точный ответ, нужно:
-
Перебрать все 44=256 вариантов выбора в строках 0–3.
-
Для каждого варианта:
-
определить, какие столбцы заняты;
-
для каждой из строк 4–7 найти множество свободных столбцов (из их 4 возможных, убрать занятые);
-
подсчитать число способов выбрать по одному столбцу из каждого множества так, чтобы все 4 столбца были разными.
-
-
Сложить все полученные числа.
Это трудоёмко вручную, но можно автоматизировать или поискать симметрии [8].
Шаг 7. Оценка снизу и сверху
-
Минимум на вариант: бывает, что для какой‑то строки 4–7 остаётся только 1 столбец (как в примере выше для строки 4). Тогда число способов ≤ 3 × 4 × 4 = 48.
-
Максимум на вариант: если для всех строк 4–7 осталось по 3 столбца и они «хорошо» пересекаются, число способов может быть до 36 (но не 81, так как столбцы должны быть разными).
Ваш пример даёт 48 на один вариант. Если таких «удачных» вариантов много, общая сумма может быть порядка 10 000–20 000.
Вывод
-
Предыдущий ответ (2 304) неверен — он основан на ошибочном допущении о константности числа способов.
-
Правильный ответ значительно больше и требует детального перебора или умного комбинаторного анализа.
-
Ваш пример показывает, что для одного из 256 вариантов есть 48 способов в строках 4–7, что уже даёт оценку снизу: 256×1=256, а реально — намного больше.
Итог: точный ответ требует перебора всех 256 случаев или нахождения симметрий/формулы. На данный момент можно утверждать, что число расстановок существенно больше 2 304 и, вероятно, близко к вашей оценке ~17 000. Для точного числа нужен программный подсчёт или более тонкий комбинаторный анализ.
и 4 выбора в строке 7;
итого 1 3 4 4 = 48 вариантов! То есть значение можно оценить как 48 250 = 12000, это гораздо больше чем ты насчитала!
Этот вопрос позволил ИИ осознать-признать свою ошибку и выдать ответ в стиле: “Точный ответ сообщить не могу, требуются тонкий комбинаторный анализ. Ваш результат ~17 000 похож на правду!”. Но она тут тоже местами врет в рассуждениях.
Промт #4 (в контексте предыдущего общения)
А ты можешь написать программу на С/С++ которая точно посчитает эти варианты перебора в этом патерне?
Ответ с идеей программы и с самой программой, которая работает
Да, конечно. Ниже — программа на C++, которая точно посчитает число допустимых расстановок галочек в заданном паттерне.
Условия задачи (напомним)
-
В каждой из 8 строк ровно одна галочка (ставится только на
X). -
Все 8 галочек — в разных столбцах (номера 0–15).
-
Структура
Xзадана явно для каждой строки.
Идея решения
-
Перебираем все варианты расстановки галочек в строках 0–3 (по 4 варианта на строку → 44=256).
-
Для каждого такого варианта:
-
отмечаем занятые столбцы;
-
для строк 4–7 формируем списки доступных столбцов (из их «родных»
X, исключая уже занятые); -
рекурсивно (или итеративно) считаем число способов поставить по одной галочке в строках 4–7 так, чтобы все столбцы были разными.
-
-
Суммируем результаты.
Код на C++
#include <iostream>
#include <vector>
// Для каждой строки — список столбцов, где стоит X
const std::vector<std::vector<int>> positions = {
{0, 1, 2, 3}, // строка 0
{4, 5, 6, 7}, // строка 1
{8, 9, 10, 11}, // строка 2
{12, 13, 14, 15}, // строка 3
{0, 4, 8, 12}, // строка 4
{1, 5, 9, 13}, // строка 5
{2, 6, 10, 14}, // строка 6
{3, 7, 11, 15} // строка 7
};
// Рекурсивная функция: считаем число способов расставить галочки в строках [start_row..7]
// used_cols — битовая маска занятых столбцов (бит i установлен, если столбец i занят)
long long countWays(int start_row, unsigned int used_cols) {
if (start_row == 8) {
return 1; // все строки обработаны
}
long long total = 0;
for (int col : positions[start_row]) {
if ((used_cols & (1U << col)) == 0) { // столбец col ещё свободен
total += countWays(start_row + 1, used_cols | (1U << col));
}
}
return total;
}
int main() {
long long total_count = 0;
// Перебираем все варианты для строк 0–3
for (int c0 : positions[0]) { // строка 0
for (int c1 : positions[1]) { // строка 1
for (int c2 : positions[2]) { // строка 2
for (int c3 : positions[3]) { // строка 3
// Формируем маску занятых столбцов после строк 0–3
unsigned int used_cols = (1U << c0) | (1U << c1) | (1U << c2) | (1U << c3);
// Считаем число способов для строк 4–7
long long ways = countWays(4, used_cols);
total_count += ways;
}
}
}
}
std::cout << "Общее число допустимых расстановок: " << total_count << std::endl;
return 0;
}
Как это работает
-
positions— массив из 8 векторов; каждый вектор содержит номера столбцов сXдля соответствующей строки. -
countWays(row, used_cols)— рекурсивная функция:-
row— текущая строка (от 4 до 7); -
used_cols— битовая маска (32‑битное целое), где битiравен 1, если столбецiуже занят; -
для каждой возможной позиции
colв строкеrow:-
если столбец
colсвободен ((used_cols & (1U << col)) == 0), -
рекурсивно вызываем
countWaysдля следующей строки, отмечая столбецcolкак занятый.
-
-
-
В
main():-
перебираем все комби��ации
(c0, c1, c2, c3)для строк 0–3; -
формируем начальную маску
used_cols; -
вызываем
countWays(4, used_cols)и накапливаем результат.
-
Оптимизация (если нужно быстрее)
-
Можно заменить рекурсию на итерацию (динамическое программирование по маскам), но для 4 строк (4–7) рекурсия вполне эффективна.
-
Можно предварительно вычислить для каждой из 256 комбинаций строк 0–3 число способов в строках 4–7 и кешировать, но в данном случае проще оставить как есть.
Запуск и результат
Скомпилируйте и запустите:
g++ -O2 program.cpp -o program
./program
Программа выведет:
Общее число допустимых расстановок: <число>
Ожидаемое значение: по вашим оценкам — около 17 000. Точный результат даст программа.
Почему это корректно
-
Перебор всех вариантов для строк 0–3.
-
Для каждого варианта — точный подсчёт допустимых расстановок в строках 4–7 с учётом всех ограничений на столбцы.
-
Нет пропусков и нет двойного счёта.
Итог: эта программа даст точный ответ на вашу задачу.
тут она действительно сгенерировала программу на С++ которая работает (загляните!) и считает правильный результат! Кстати без рекурсии тоже не обошлось. Но поскольку размер сегмента меньше битности стандартной аппаратной платформы (32 бита), она смогла применить битовые операции и маски вместо побайтового сравнения.
Но этот вариант с циклами позволяет легко выводить статистики, например если запустить алгоритм для каждого из 16 (теперь! Вместо 9 для 3х случая) вариантов заданных в первых двух (а не трех) строчках четверичного случая, но не до конца таблицы, а до конца НХ сегмента и выяснилось, что варианта получается все также только два 912 и 1106, хотя если посчитать варианты расстановок которые приходятся на предопределенные значения во всех 4-х горизонтальных строчках НХ сегмента вариаций перестановок стало больше 48, 64, 72, 81, тогда как для 3х случая для предопределенных заполненных трех ячеек в горизонтальных линиях было только два варианта 6 и 8. Программа с циклами for позволяет простые модификации чтобы получить такую статистику :
// Перебираем все варианты для строк 0–3
for (int c0 =0;c0<4;c0++) { // строка 0
for (int c1 =0;c1<4;c1++) { // строка 1
long long sum3 = 0;
for (int c2 =0;c2<4;c2++) { // строка 2
for (int c3 : positions[3]) { // строка 3
// Формируем маску занятых столбцов после строк 0–3
unsigned int used_cols = (1U << c0) | (1U << (c1+4)) | (1U << (c2 + 8)) | (1U << c3);
// Считаем число способов для строк 4–7
long long ways = countWays(4, used_cols);
total_count += ways;
sum3 = ways;
}
std::cout << indx++ << "; CNT "<< c0 << c1<< "=" << sum3 << ";" << total_count << std::endl;
}
//std::cout << indx++ << "; CNT "<< c0 << c1<< "=" << sum3 << ";" << total_count << std::endl;
}
}Интересно, насколько быстро можно заметить все изменения по отношению к исходному алгоритму и/или убедиться что изменения корректны и не влияют на результат вычисления?
Тут, например, достаточно хорошо видно, что можно обойтись без первой половины таблицы, но корректно исправить алгоритм при таком изменении таблицы констант не совсем тривиальная задача.
Если вы попробуете адаптировать этот вариант для исследования статистики НХ сегмента любого Nx случая вы поймете насколько это не тривиальная задача, так как таблицы вручную писать очень не хочется, да и не надежно это. А еще надо как то управлять количеством вложенных циклов. И с этими проблемами никакая рекурсия вам справиться не поможет.
Но в любом случае для серьезного анализа нужно исследовать статистику доступных вариантов перестановок по ключевым сегментам, а потом анализировать статистику наложения этих перестановок через “диагональные” зависимости. Возможно можно получить какую-то аналитику (а не статистику) при рассмотрении в обратном направлении, например исключив сегменты с горизонтальными ячейками разрешения. В общем задача остается открытой для дальнейшего анализа и для разработки программных и/или теоретических-математических инструментов такого анализа.
Автор: rukhi7
Источник [9]
Сайт-источник BrainTools: https://www.braintools.ru
Путь до страницы источника: https://www.braintools.ru/article/23083
URLs in this post:
[1] @vvvphoenix: https://www.braintools.ru/users/vvvphoenix
[2] вот его последняя статья: https://habr.com/ru/articles/893542/
[3] зрения: http://www.braintools.ru/article/6238
[4] математически: http://www.braintools.ru/article/7620
[5] ошибку: http://www.braintools.ru/article/4192
[6] логику: http://www.braintools.ru/article/7640
[7] Интеллект: http://www.braintools.ru/article/7605
[8] симметрии: http://www.braintools.ru/article/3088
[9] Источник: https://habr.com/ru/articles/974776/?utm_source=habrahabr&utm_medium=rss&utm_campaign=974776
Нажмите здесь для печати.