Азбука тензорных сетей, часть 2: тензорный поезд из кружочков и палочек

На связи вновь Алексей Капранов, архитектор-исследователь в команде квантовых вычислений Cloud.ru ^[1]. В первой части ^[2] мы узнали, что такое тензорные сети, познакомились с графическим представлением, вспомнили основные операции и подумали над алгоритмической сложностью.

Прошлая статья была подготовительной и немного философской преамбулой. Сегодня мы продолжим знакомиться с тензорными сетями и наконец-то доберемся до представления тензорного поезда, которое получим при помощи сингулярного разложения.

Сингулярное разложение

Для читателей, знакомых с ML/AI, существование сингулярного разложения ^[3] (Singular Value Decomposition (SVD)) не является каким-то сюрпризом или неожиданностью, как и вообще наличие задачи понижения размерности. Сейчас мы поговорим, что же это за разложение такое и как оно работает.

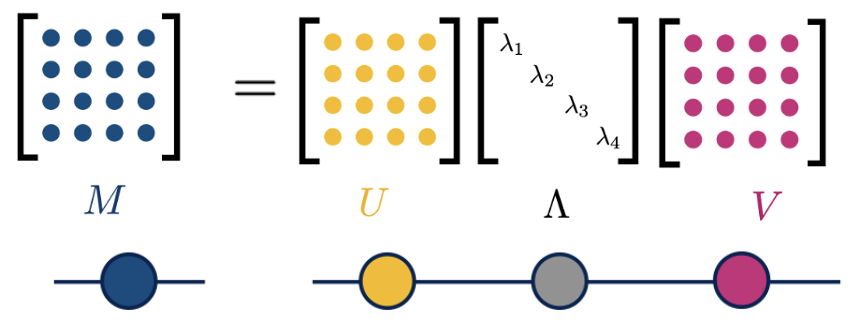
Есть строгое утверждение: любую матрицу можно представить в виде произведения трех матриц. На картинке приведен пример такого разложения для произвольной матрицы. Матрицы и являются унитарными ^[4], а — это диагональная матрица, состоящая из сингулярных чисел. Сразу отмечу, что на картинке и в примере я буду использовать квадратные матрицы в силу простоты и наглядности, но помните: это разложение справедливо и для прямоугольных матриц.

Усечение

Главным преимуществом такого разложение является возможность провести так называемое усечение. В чем оно заключается? Представим, что мы выполнили сингулярное разложение матрицы таким образом, что в диагональной матрице сингулярные значения располагаются в порядке убывания, то есть. Теперь будем приравнивать сингулярные значения к нулю, начиная с самых маленьких. В результате мы получим матрицу, близкую к исходной. Мы можем контролировать, насколько она будет близка, выбирая, сколько сингулярных значений занулить. Если же оставить все значения на месте, то такое приближение ничем не будет отличаться от исходной матрицы, потому что SVD разложение является точным. Давайте рассмотрим эту процедуру подробнее и разберем на примере.

Предположим, что мы работаем со все той же матрицей. Нам не хочется хранить кучу элементов, мы хотим иметь низкоранговую аппроксимацию (далее поговорим, что это и зачем) и радоваться жизни. Поэтому сначала приравниваем к нулю самое маленькое сингулярное значение

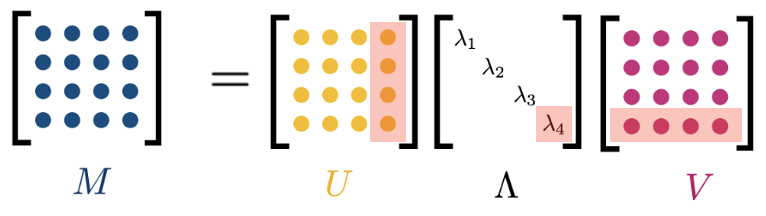
Так как, то правый столбец унитарной матрицы и левая строка унитарной матрицы тоже зануляются и исчезают из разложения, как это изображено на рисунке выше.

Можно пойти дальше и приравнять к нулю уже следующее сингулярное значение Тогда из разложения исчезнет еще один столбец матрицы U и еще одна строка матрицы

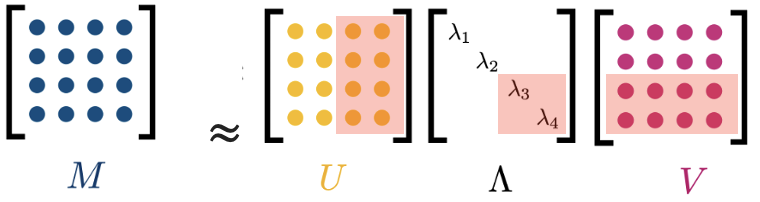
Мы не хотим останавливаться, мы хотим дальше умножать на ноль, поэтому приравниваем к нулю Тогда из нашего разложения исчезают еще один столбец и одна строка

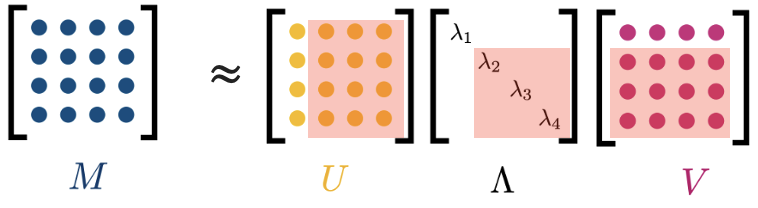
В результате такой процедуры у нас осталось только одно сингулярное значениеи по строке и столбцу в матрицахисоответственно. Дальше «выкидывать» сингулярные значения мы не можем, так как иначе просто получим полную нулей матрицу, и нам надо остановиться, пока остановка не стала последней.

Норма Фробениуса

Теперь мы умеем строить низкоранговую аппроксимацию произвольной матрицы, но как нам понять, что мы выбрали правильное приближение? Почему мы должны выкинуть именно два сингулярных значения, а не одно или три? Надо как-то оценивать, насколько близки матрицы, и для этого нет способа лучше, чем норма Фробениуса. Она определяется следующим образом

где — это сингулярные значения матрицы , которые являются действительными положительными числами.

Обремененные этими знаниями, рассмотрим еще один игрушечный пример. Пусть у нас есть следующая матрица

Выполнив сигулярное разложение, получаем

Посмотрим, как будут отличаться нормы матриц, если мы выполним процедуру усечения с одним и двумя сингулярными значениями.

Под обозначением будем понимать восстановленную матрицу, где индекс — это количество оставшихся сингулярных значений. Выкинув самое малое значение мы получаем разницу норм Если же занулить еще и , то разница норм . Таким образом, мы получаем контролируемое приближение исходной матрицы .

Подводные камни

Задача эффективного понижения размерности напрямую зависит от количества сингулярных значений, которые мы можем «выкинуть» без превышения наперед заданной нами ошибки ^[5]. Из примера выше можно заметить, что мы без особого для себя урона можем избавиться от относительно небольших сингулярных значений. Тогда сразу назревает проблема – если у нас достаточно много близких по абсолютной величине сингулярных значений, то без ущерба для точности восстановленной матрицы мы сможем «выкинуть» только очень малую их часть .

Скажу честно, в этом случае таким подходом просто так не отделаешься и надо его комбинировать с другими методами и вообще проявить стоицизм в этом вопросе. Но такая ситуация достаточно редкая, и зачастую мы имеем дело с экспоненциально малым числом «больших» сингулярных значений и экспоненциально большим числом «малых» сингулярных значений.

Типичный пример такой ситуации изображен на картинке ниже, которую любят приводить в обзорах по тензорным сетям. Это пример использования сингулярного разложения для сжатия изображения. Крайне правый график — это величина сингулярного числа относительно его порядкового номера, отсортированная по убыванию. Мы видим, что есть относительно небольшое число «значимых» для успешного восстановления картинки сингулярных значений, а остальные можно выкинуть в силу малости.

Именно такая процедура и изображена на рисунке выше. Если мы оставим только 1% сингулярных значений, то мы сможем восстановить исходную картинку, но лишь в общих чертах и достаточно «шакально». Если же оставим уже 5% сингулярных значений, то восстановленное изображение уже мало будет отличаться от оригинала (не кидайтесь камнями, я близорукий).

Tensor Train

Поздравляю, теперь вы обладаете необходимым минимумом знаний, чтобы получить самое простое и наиболее изученное тензорное разложение, которое в зависимости от предметной области называется Tensor Train (TT) decomposition или Matrix Product State (MPS). Я буду использовать именно понятие Tensor Train, так как мы здесь обсуждаем скорее компьютерные науки, нежели квантовую физику.

В первой части ^[2] я говорил про мотивацию ^[6] к использованию тензорных разложений, давайте еще раз ее вспомним. Мы имеем дело с так называемым проклятием размерности, когда вычислительная сложность задачи растет как , где — это число параметров, а — это размерность. Использование представления TT позволяет сделать скейлинг сложности линейным по и то есть Внимательный читатель может поймать меня за руку и справедливо заметить, что тут появилась еще одна буква . Она означает максимальный ранг разложения матрицы, который получается в ходе сингулярного разложения (здесь ранг в смысле числа линейно-независимых строк/столбцов). То есть мы должны «выкидывать» достаточное количество сингулярных значений, чтобы эффективно использовать ТТ и был относительно небольшим. Что такое «достаточное» это отдельный вопрос, который определяется фактурой задачи, то насколько точно мы можем восстановить матрицу и как вообще ведут себя ее сингулярные значния. Здесь я уклончиво обойду это стороной, так как мы все-таки обсуждаем общую концепцию, а не конкретный случай.

Сейчас мы получим это представление для произвольного тензора 6-го ранга, а потом еще раз обдумаем, что же это все значит и как проще это представить у себя в голове.

Алгоритм приведения произвольного тензора к виду TT

Мы инициализируем произвольный тензор 6-го ранга с размерами и знаем, как изобразить его графически — это овал с 6 палочками (здесь и далее будет дан код, соответствующий тензорной диаграмме). То есть

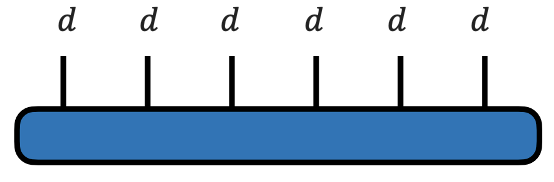
import numpy as np
# задаем размерность d, пусть она будет равна 5
d = 5
# инициализируем случайный тензор 6-го ранга
M = np.random.rand(d,d,d,d,d,d)
# проверим его размер
print(M.shape) # (5, 5, 5, 5, 5, 5)

У нас уже есть инструмент для декомпозиции с контролируемой точностью, но он работает для матриц. Значит, нам надо просто превратить тензор в матрицу, сделать это мы можем с помощью reshape’a. Графически это будет выглядеть так, как будто мы оставили одну палочку, а другие пять штук соединили в одну большую.

# преобразуем тензор в матрицу
M = M.reshape(d,d**5)
# проверяем размер
print(M.shape) # (5, 3125) = (5, 5**5)

Теперь у нас есть матрица и можем выполнять сингулярное разложение. Сразу предположим, что мы из некой экспертной оценки знаем ранг разложения, пусть он будет

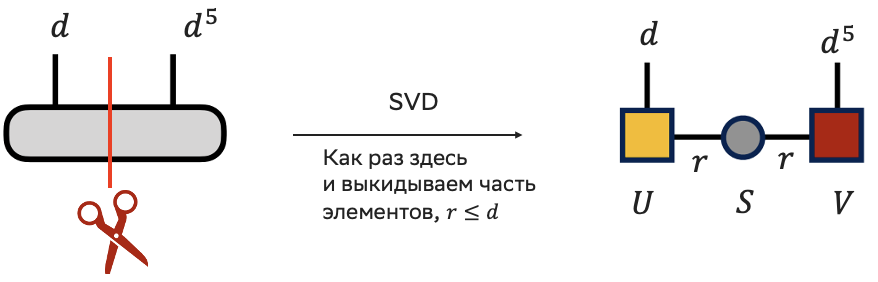
from numpy import linalg as LA
# выполняем SVD 
U,S,V = LA.svd(M, full_matrices=False)
# проверяем размерности
print(U.shape) # (5, 5)
print(S.shape) # (5, )
print(V.shape) # (5, 3125)
print(M.shape) # (5, 3125)
# выполняем усечение до ранга r
# пусть он будет равен 4
r = 4
U = U[:,:r]
S = np.diag(S[:r])
V = V[:r,:]
# проверяем размерности
print(U.shape) # (5, 4)
print(S.shape) # (4, 4)
print(V.shape) # (4, 3125)
# можно также убедиться, что мы восстанавливаем 
# ту же матрицу M, если раскомментируем строчки ниже
# M = U @ S @ V
# print(M.shape) # (5, 3125)

Отмечу, что в numpy сингулярные значения располагаются в порядке убывания, как в примерах, которые мы рассматривали выше, поэтому в коде выше именно такое усечение.

Отлично, мы наплодили сущностей. Давайте теперь думать, что нам делать дальше. По аналогии с матричным разложением мы хотим получить некую свертку нескольких тензоров. Для этого нам придется перемножить центральную диагональную матрицу сингулярных чисел с матрицей слева или справа. Мы будем сворачивать с правой матрицей из соображений хода операций слева направо.

# перемножаем центральную матрицу с правой матрицей 
SV = S @ V
# проверяем размерности 
print(U.shape) # (5, 4) 
print(SV.shape) # (4, 3125)

Про выбор кого с кем перемножить

Здесь я должен сделать небольшое отступление. Из-за того, что мой выбор перемножения не является единственным, не единственным будет и TT разложения. Вопросы выбора нужных перемножений (слева или справа) называется калибровкой тензорной сети, и это отдельный серьезный вопрос, которого мы касаться не будем. Просто знайте, что разложение можно получить не единственным образом.

Вообще, для реализации таких гибких хитрых калибровок часто вообще не перемножают диагональную матрицу с остальным, а оставляют ее как есть. Даже в этом случае мы все равно получим ТТ разложение. Просто для новичка эта тема сложная, а еще мне лень рисовать в два раза больше кружочков и палочек.

Кажется, мы начинаем наблюдать что-то похожее на тензорное разложение. У нас появился отдельный тензор который принято называть ядром, и есть весь остальной тензор Теперь наша задача разделить этот большой тензор на ядра, ровно как мы и делали до этого. Давайте теперь получим отдельно ядро и тензор

Нам надо проделать аналогичную процедуру, то есть свернуть в матрицу, выполнить сингулярное разложение и развернуть обратно в тензор, факторизуя дополнительное ядро

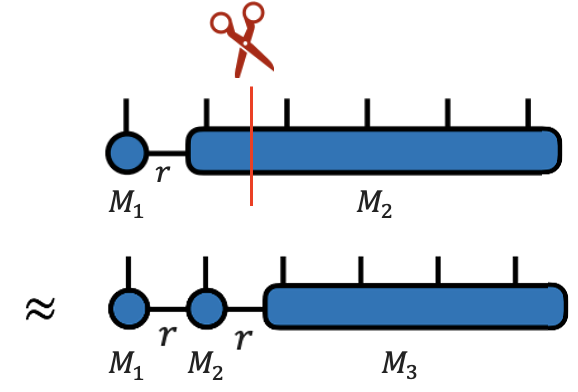
# сворачиваем M2 в матрицу
# обратите внимание, что я сворачиваю два индекса слева
M2 = M2.reshape(r*d, d**4)
# выполняем SVD и сразу делаем усечение по r
U,S,V = LA.svd(M2, full_matrices=False)
U = U[:,:r]
S = np.diag(S[:r])
V = V[:r,:]
# проверяем размерности 
print(U.shape) # (20, 4)
print(S.shape) # (4, 4)
print(V.shape) # (4, 625)
# перемножаем центральную матрицу S
# и правую матрицу V
SV = S @ V
# теперь мы разворачиваем матрицу U в ядро M2
# и разворачиваем матрицу SV в тензор M3
M2 = U.reshape(r,d,r)
M3 = SV.reshape(r,d,d,d,d)
# проверяем размерности 
print(M2.shape) # (4, 5, 4)
print(M3.shape) # (4, 5, 5, 5, 5)

Теперь мы должны повторить все это для . Код я прикладывать не буду, все с точностью до замены индексов (2, 3) в букве на (3, 4).

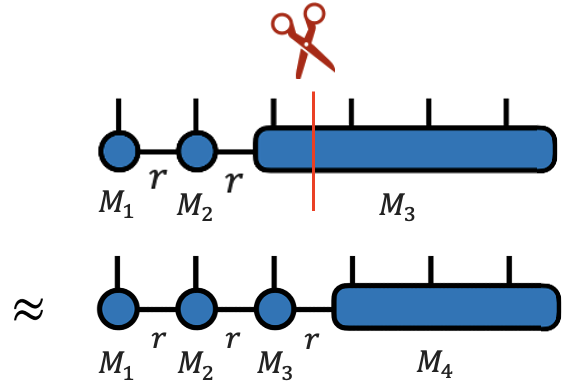
Продолжая разрезать тензор, мы получим все шесть ядер

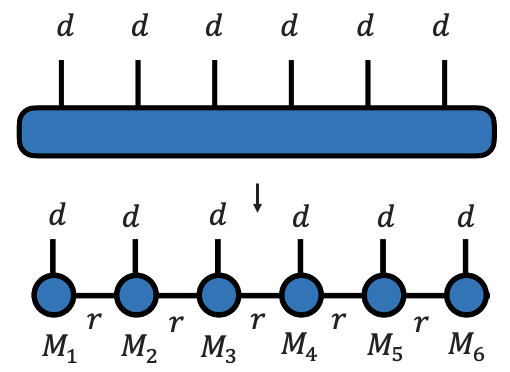
Вот мы и получили TT-представление! Сразу оговорюсь, что в данном учебном примере мы в сингулярном разложении «обрезали» на одном и том же значении рангадля простоты картины. Очевидно, что в общем случае мы можем выбирать совершенно разные ранги между любыми ядрами, но в асимптотике мы, конечно, учитываем только максимальный ранг.

Если мы хотим представить TT в своем воображении, то стоит подумать, почему же в квантовой физике у этого разложения другое название — Matrix Product State. Ключевые слова здесь Matrix и Product, то есть каждый элемент тензора представляется в виде произведения матриц. Мне очень нравится следующая иллюстрация из выступления ^[7] Александра Новикова.

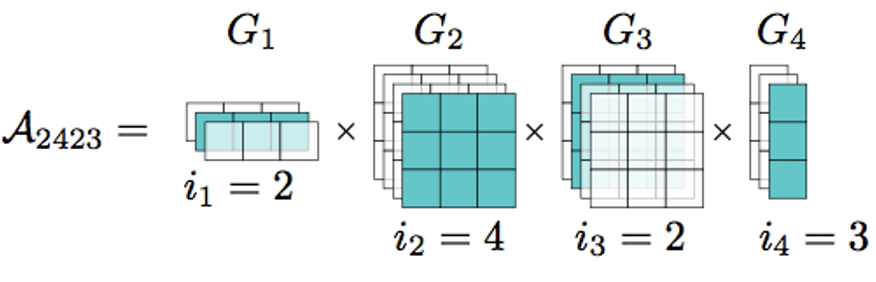
Что же тут нарисовано? По краям тензорного разложения расположены матрицы, а между ними уже тензора 3-го ранга. Когда мы фиксируем какой-то индекс в матрице, получаем вектор, а в случае тензора третьего ранга получаем матрицу. То есть каждый элемент тензора мы можем получить через произведения векторов и матриц, которые лежат по нужному «адресу».

Про алгоритмическую сложность

Для полноты картины давайте получим вычислительную сложность, а то я везде привожу асимптотику, но до этого мы не могли ее вывести. С нашим багажом знаний мы получим этот результат почти «бесплатно». Достаточно просто посмотреть на картинку тензорной сети и сразу смекнуть, что к чему.

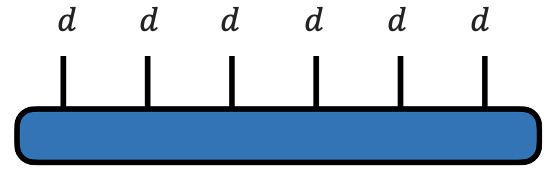
Посмотрим еще раз на начальный тензор. Что мы видим? Мы видим синий овал и шесть палок. Поскольку они все «торчат» из одного тензора, то по правилам из первой части ^[2], мы заработаем асимптотику , а в общем случае .

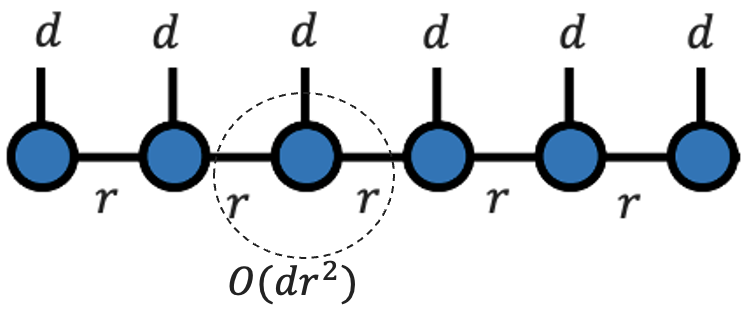
Мощь представления тензорного поезда как раз и заключается в том, что мы можем как бы отдельно работать с ядрами. То есть если мы последовательно будем выполнять операции с каждым их них, то получим сложность . В общем же случае для ядер мы получаем .

Про алгоритмическую сложность SVD

Мы научились получать ТТ-представление для произвольного тензора при помощи сингулярного разложения, однако сейчас алгоритмы проектируют таким образом, чтобы сразу же работать с тензорным разложением. То есть не выполнять работу по приведению данных в ТТ-формат.

Однако все равно часто приходится прибегать к сингулярному разложению и полезно знать, что его алгоритмическая сложность . Если же нам надо выделить какие-то значений, то мы можем ее сократить до .

К каким итогам мы пришли?

Мы получили TT-представление тензора, но что дальше? Хочется подробнее рассказать про операции с тензорами в TT-формате (они есть, причем быстрые и достаточно дешевые, см. выступления И. Оселедеца и А. Новикова), максимальные значения рангов, возникающие проблемы и самые свежие результаты, а также ограничения и пути их обхода. Особый интерес ^[8] вызывает рассказ о более сложных тензорных представлениях. Но объять необъятное это, наверное, NP-сложная задача, а две эти статьи и так слишком разрослись. Так что ограничусь небольшим перечислением основных применений и проблем такого подхода.

Из-за своей профессиональной деформации, в первую очередь я упомяну квантовые вычисления, где применение таких методов является почти безальтернативной необходимостью для симуляции работы квантовых устройств. Мы живем в эпоху шумных квантовых вычислений (почитайте отличную работу ^[9] моего соратника Михаила Ремнева (@maremnev ^[10]) про квантовые компьютеры), а значит, исследовательская работа в этом направлении не может обойтись без методов тензорных сетей, которые позволяют победить «проклятие размерности» квантового мира.

Сейчас появляется все больше работ, посвященных использованию TT-формата и более сложных представлений в ML/DL. Это связано с тем, что результаты исследований постепенно просачиваются через стены лабораторий и R&D отделов в чуть более широкие массы (по крайней мере, я надеюсь на это). Я перечислю парочку интересных результатов за последние год-два.

В работе ^[11] авторы использовали квантово-вдохновленный подход, идеологически аналогичный TT, для компрессии корреляционного пространства модели. Тесты на LlaMA-7B показали снижение памяти ^[12] на 93% и количества параметров на 70% c ускорением обучения ^[13] на 50% и инференса на 25% при минимальных потерях точности в 2–3%.

Можно добиться сокращения числа параметров и ускорения обучения для сверточных нейронных сетей (ссылка 1 ^[14] и ссылка 2 ^[15]). Также тензорные алгоритмы дают значительное понижение сложности с экспоненциальной на линейную в механизмах внимания ^[16] (ссылка ^[17]).

Кратко скажу про основные ограничения именно TT-формата. В первую очередь, не все тензоры хорошо «жмутся», то есть никто не гарантирует, что мы сможем «выкинуть» достаточно много сингулярных значений. Второе — ограничения по максимальному рангу разложения. Он может оказаться достаточно большим для сильно связанных систем, что не позволит сильно понизить размерность задачи. Наконец, зачастую требуется тонкая ручная настройка гиперпараметров, что бывает значительно усложняет работу. Однако даже простое использование TT-формата без применения усечения (то есть при ), зачастую позволяет существенно улучшить жизнь.

Теперь вы уже знаете достаточно и можете самостоятельно ознакомиться с так любимыми мной текстом выступления ^[18] Ивана Валерьевича Оселедеца в Яндексе или посмотреть запись выступления ^[7] Александра Новикова на семинаре ФКН ВШЭ.

Всем спасибо за внимание! Надеюсь, было понятно и интересно. До новых встреч, Хабр!

Благодарности

Эти статьи не появились бы без тех, кто помогал мне с редактурой. Это мой коллега Александр Мальцев (@pulk ^[19]), направление контент-маркетинга Cloud.ru (Анастасия Тутова (@tutova_tut ^[20]), Марина Митясова и Елизавета Иванова) и редакция Хабра (Люси Шибарова).

Помимо редактуры есть люди, с которыми в обсуждениях удалось сформулировать объяснения этой темы в том виде, в котором вы ее читаете. Это — Михаил Ремнев (@maremnev ^[10]), Павел Бузин (@pbuzin ^[21]), Глеб Шувалов, Екатерина Кривцова (@kriwzowa ^[22]) и Екатерина Мицкевич.

Спасибо всем вам.

<spoiler>