Машина, которая никогда не останавливается: как одно предложение поставило предел человеческому познанию
Аннотация
В 1936 году Алан Тьюринг, пытаясь формализовать пределы вычислений, сформулировал вопрос, навсегда изменивший не только компьютерную науку, но и наше понимание границ познания. Этот вопрос — известная как «Проблема остановки» — звучит обманчиво просто: можно ли создать алгоритм, который, анализируя код любой программы и её входные данные, заранее и безошибочно определит, завершится ли её работа или же она уйдёт в бесконечный цикл? Казалось бы, речь идёт о чисто технической задаче, мечте каждого программиста об идеальном отладчике. Однако ответ Тьюринга, уместившийся в элегантное и почти язвительное доказательство от противного, оказался оглушительным: нет, такой алгоритм принципиально невозможен. В этой статье мы не только разберём суть этого гениального доказательства, которое построено на самореференции и логическом парадоксе [1], подобном «лжецу», но и визуализируем его ход с помощью наглядного кода в MATLAB, превратив абстрактную логику [2] в динамическую демонстрацию. Мы увидим, как гипотетическая «всезнающая» программа H неминуемо запутывается в сетях, расставленных специально сконструированной программой-провокатором , приводя к неразрешимому противоречию в любом исходе. Это открытие — не просто академическая курьёзность. Оно устанавливает фундаментальный, алгоритмический предел: существуют чётко поставленные вопросы, на которые мы никогда не получим однозначный «да» или «нет» от любой вычислительной машины. Мы проследим глубокую связь этого результата с теоремой Гёделя о неполноте, обсудим другие неразрешимые проблемы, такие как проблема соответствия Поста, и затронем трезвые последствия для современной разработки, верификации программ и даже для мечтаний о создании всесильного искусственного интеллекта [3]. Эта история — о том, как осознание непреодолимой границы стало одним из самых мощных интеллектуальных достижений человечества, чётко очертив то, что мы можем знать, и указав на бескрайние области того, что мы знать не в силах.
Представьте 1936 год. Мир стоит на пороге войны, но в тишине кабинетов происходит тихая революция. Алан Тьюрингу — молодому, ещё не легендарному математику [4] — поручают, казалось бы, сухую и абстрактную задачу: определить, что именно можно вычислить с помощью механического процесса, алгоритма. Это был вопрос из области основ математики, часть программы «формализации» — попытки превратить всю математику в безупречную логическую машину, где истинность любого утверждения можно было бы проверить автоматически.
Именно в этой работе Тьюринг создаёт свою абстрактную «машину» — прообраз всех современных компьютеров. Но среди технических деталей возникает один, на первый взгляд, побочный и практичный вопрос. Он звучит так: «Можем ли мы, просто взглянув на описание программы и её входные данные, заранее предсказать, завершит ли она свою работу, выдав результат, или же будет работать вечно, зациклившись?»
Это и есть Проблема остановки (Halting Problem). В её основе — не просто любопытство. Это вопрос о самой природе логики и её предсказуемости. Если бы на него можно было ответить «да», мы бы получили ключ к абсолютному контролю над цифровым миром. Вы представляете?
-
Идеальный отладчик, который одним взглядом на код находит все потенциальные бесконечные циклы и зависания.
-
Абсолютный антивирус, который безошибочно отличает вредоносный код от безопасного, просто анализируя его логику.
-
Всемогущий верификатор, который доказывает правильность любой программы, скажем, для управления атомной станцией или медицинским аппаратом.
Это была бы утопия формальной логики — мир, в котором любое поведение [5] программы можно было бы предсказать, не запуская её. Мечта, лежащая в самой основе идеи «совершенной машины».
Но Тьюринг, применив оружие чистой логики против самой себя, разбил эту мечту. Его доказательство, короткое и невероятно элегантное, показало, что такой волшебный анализатор не может существовать в принципе. Ответ на п��облему остановки — «нет». И это «нет» — не временное ограничение наших технологий. Это фундаментальный, математический барьер, встроенный в саму ткань логики и вычислений.
Почему же это открытие, доказавшее невозможность чего-либо, стало одним из краеугольных камней всей компьютерной науки? Потому что, осознав непреодолимую границу, мы, наконец, смогли по-настоящему понять силу и природу того, что возможно. Давайте разберем эту логическую ловушку, в которую попадает любая претендующая на всезнание машина.
Итак , начнем , доказательство Тьюринга — это не атака грубой силой, а интеллектуальное дзюдо. Он использует силу гипотетического «всезнающего» алгоритма против него самого, заставляя его споткнуться о собственные предположения.
Представим, что волшебная программа всё-таки существует. Она — чёрный ящик. Вы подаёте ей на вход исходный код любой другой программы
и её входные данные
. После некоторого анализа
выдаёт безошибочный вердикт:
-
1 (Истина): «
завершится».
-
0 (Ложь): «
никогда не завершится (зациклится)».
Теперь сконструируем программу-провокатор . Её логика — это логика бунтаря, который поступает строго наоборот тому, что предсказывает оракул
.
Пусть получает на вход описание некоторой программы
. Что она делает?
-
спрашивает у
: «Что будет, если программе
скормить на вход… её же собственный код? Завершится ли вычисление
?» (Здесь рождается самореференция — ключевой момент, роднящий этот парадокс с утверждением «Это высказывание — ложь»).
-
получает ответ от
и…
-
Если
говорит: «Да,
остановится», — тогда
, получив такой прогноз, сознательно уходит в бесконечный цикл и никогда не останавливается.
-
Если
говорит: «Нет,
не остановится», — тогда
, вопреки прогнозу, немедленно и корректно завершает свою работу.
-
— это логическая мина, начиненная противоречием. Её единственная цель — опровергнуть предсказание
.
Формально-алгоритмический уровень
Давайте формализуем эту конструкцию, чтобы противоречие стало математически очевидным.
-
Гипотеза: Существует вычислимая функция
. Для любой программы
и входных данных
:
, если программа
на входе
останавливается.
, если программа
на входе
не останавливается.
(Здесь
может быть и кодом программы, и её данными, так как в машине Тьюринга и то, и другое — суть строки символов).
-
Конструкция провокатора: Теперь определим программу
, код которой зависит от
. На псевдокоде её логика выглядит так:
ФУНКЦИЯ P(вход x):
ЕСЛИ H(x, x) == 1 ТО
ПЕРЕЙТИ В ШАГ 2 // Уходим в бесконечный цикл
ИНАЧЕ
ЗАВЕРШИТЬ РАБОТУ // Корректно останавливаемся-
Критически важно: программа
вполне конструктивна. Если бы
существовала, то и
можно было бы запрограммировать — это просто комбинация вызова
и условного оператора.
-
Фатальный вопрос: Что произойдет, если мы подадим саму программу
ей же на вход? То есть, рассмотрим вычисление
.
Подставим
в качестве аргумента в её же собственную логику и проанализируем оба возможных ответа оракула
.
-
Случай А: Предположим,
. Согласно определению
H, это означает: «Вычислениеостановится».
Но если мы теперь реально запустим, то, выполняя её код, мы увидим: поскольку
, программа
выполнит ветку
и уйдет в бесконечный цикл. Следовательно,
не остановится.
-
H(P, P) = 1 => P(P) не остановится. // ПРОТИВОРЕЧИЕ.Случай Б: Предположим, . Это означает: «Вычисление
не остановится (зациклится)».Теперь запустим
. Её код, получив результат
, пойдет по ветке
и немедленно завершится. Следовательно,
остановится.
H(P, P) = 0 => P(P) остановится. // ПРОТИВОРЕЧИЕ.-
Мы приходим к логическому тупику. Не существует такой функции
, которая могла бы дать непротиворечивый ответ на вопрос об остановке
.
-
Если она говорит «стоп», программа уходит в вечный цикл.
-
Если она говорит «вечный цикл», программа торжественно останавливается.
-
Следовательно, наша исходная гипотеза неверна. Проблема остановки алгоритмически неразрешима. Универсальной программы , способной предсказать судьбу любой другой программы, не существует в принципе. Это не ограничение наших инженерных способностей — это фундаментальный закон мироздания вычислений, такой же непреложный, как закон сохранения энергии в физике.
Теоретическое доказательство неразрешимости проблемы остановки — это шедевр логики. Но что, если мы попробуем его смоделировать? Что, если мы, невзирая на доказанную невозможность, попытаемся создать прототип оракула и программы-провокатора
? Именно это мы сейчас и сделаем в MATLAB, чтобы увидеть парадокс воочию, в динамике вычислений и графиков.
Наша цель — не создать невозможное, а визуализировать сам момент возникновения противоречия. Мы построим символическую модель, где программы — точки в пространстве, их поведение [6] — математические поверхности, а логическая ловушка — разрыв на графике. Этот эксперимент превратит сухую формулу в наглядную драму.
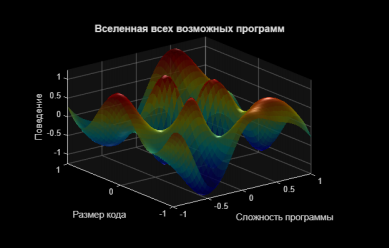
Сначала создадим контекст — абстрактное пространство, где живут наши программы. В реальности множество всех программ дискретно и бесконечно, но для наглядности представим его как непрерывную сложную поверхность (Рис. 1, подграфик 1). Её «складки» и «пики» символизируют невероятное разнообразие возможных поведений: где-то программа завершается быстро, где-то — входит в цикл, где-то — демонстрирует хаотичное вычисление.
% 1. СИМВОЛИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВСЕЛЕННОЙ ПРОГРАММ
figure('Position', [100 100 1200 800]);
subplot(2,2,1);
% Матрица программ и их поведения
N = 50;
[X, Y] = meshgrid(linspace(-1, 1, N));
R = sqrt(X.^2 + Y.^2); % Исправлена опечатка: .*2 -> .^2
Theta = atan2(Y, X);
Z = sin(5*R).*cos(3*Theta) + 0.3*cos(7*X).*sin(5*Y);
surf(X, Y, Z, 'EdgeColor', 'none', 'FaceAlpha', 0.8);
title('Вселенная всех возможных программ', 'FontSize', 12);
xlabel('Сложность программы'); ylabel('Размер кода'); zlabel('Поведение');В эту вселенную мы помещаем гипотетического оракула . Представим его как классификатор, который проводит границу через пространство всех пар «программа-вход» (Рис. 1, правый верхний угол). По одну сторону — программы, которые, по его «мнению», остановятся (синяя область), по другую — которые зациклятся (красная область). Плавная красная линия — это «граница решения» оракула, результат его «всеведения».
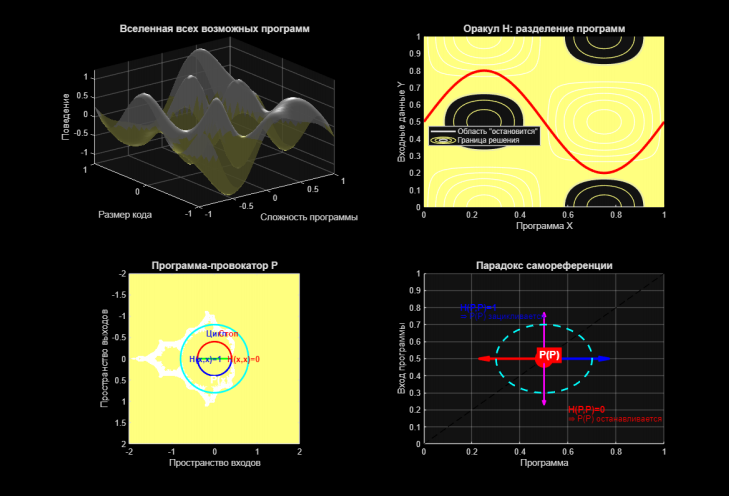
H. Он делит все возможные вычислительные задачи на два класса. Плавная граница символизирует его идеальное, по нашему предположению, знание. % 2. ГИПОТЕТИЧЕСКИЙ ОРАКУЛ H
subplot(2,2,2);
hold on;
[X_h, Y_h] = meshgrid(linspace(0,1,100));
Z_h = sin(2*pi*X_h).*cos(2*pi*Y_h) + 0.5;
contourf(X_h, Y_h, Z_h, [0 0], 'LineWidth', 2);
decision_boundary = 0.5 + 0.3*sin(2*pi*X_h(1,:));
plot(X_h(1,:), decision_boundary, 'r-', 'LineWidth', 3);
title('Оракул H: разделение программ', 'FontSize', 12);
xlabel('Программа X'); ylabel('Входные данные Y');
legend({'Область "остановится"', 'Граница решения'}, 'Location', 'best');Теперь построим главного героя нашей драмы — программу . Её логика самореферентна и коварна. Мы визуализируем её не как код, а как фрактальную структуру — множество Мандельброта (Рис. 1, левый нижний угол). Это глубоко символично: фракталы являются эталоном вычислимой, но бесконечно сложной структуры, а их граница — место, где мельчайшие изменения ведут к кардинально разным исходам (остановка или цикл). Это идеальная метафора для
.
Поверх фрактала мы накладываем схему её алгоритма: внешний контур (циан), внутри — развилка: синяя ветвь (действие при : уход в цикл) и красная ветвь (действие при
: остановка).
% 3. ПРОГРАММА-ПРОВОКАТОР P
subplot(2,2,3);
% ... (код генерации множества Мандельброта) ...
imagesc(x_p, y_p, log(escape+1));
colormap(hot);
% ... (код рисования логической схемы P) ...
text(-0.1, 0.5, 'P(x):', 'Color', 'w', 'FontSize', 12, 'FontWeight', 'bold');
title('Программа-провокатор P', 'FontSize', 12);
xlabel('Пространство входов'); ylabel('Пространство выходов');Примечание :Рис. 1 (левый нижний угол): Программа , представленная как фрактал (Множество Мандельброта). Её внутренняя логическая структура (схема справа) показывает две взаимоисключающие ветви, зависящие от вердикта
.
Кульминация наступает, когда мы задаем роковой вопрос: «А что если ?». Это точка самореференции, где программа применяется к самой себе. На графике (Рис. 1, правый нижний угол) это диагональ
. Точка
лежит на этой диагонали.
И здесь оракул сталкивается с дилеммой, представленной синим и красным векторами, устремленными в противоположные стороны.
-
Синий вектор (
): Если оракул предсказывает остановку,
по своей логике уходит в цикл, «убегая» от предсказания влево (в область не-остановки).
-
Красный вектор (
): Если оракул предсказывает цикл,
немедленно останавливается, «убегая» от предсказания вправо (в область остановки).
% 4. ПАРАДОКС И ПРОТИВОРЕЧИЕ
subplot(2,2,4);
plot(t, t, 'k--', 'LineWidth', 1); % Диагональ самореференции
plot(0.5, 0.5, 'ro', 'MarkerSize', 20, 'MarkerFaceColor', 'r'); % Точка P(P)
quiver(0.5, 0.5, 0.3, 0, 'b', 'LineWidth', 3); % Вектор противоречия H=1
quiver(0.5, 0.5, -0.3, 0, 'r', 'LineWidth', 3); % Вектор противоречия H=0
title('Парадокс самореференции', 'FontSize', 12);Примечание : Рис. 1 (правый нижний угол): Точка парадокса P(P) на диагонали самореференции. Противоречивые векторы показывают, что любой ответ H приводит к обратному результату, создавая логический разрыв.
Давайте попробуем симулировать работу такого оракула для множества программ. Создадим матрицу, где элемент (i, j) — это решение H для i-й программы на j-м входе (Рис. 2, левая часть). На диагонали этой матрицы, где программа применяется сама к себе, мы искусственно встроим логику P, приводящую к противоречию. На графике это проявляется как сбой на диагонали: фактические результаты (синие кружки) не следуют плавной ожидаемой зависимости (красный пунктир), а в точке P(P) (красный круг) происходит катастрофическое расхождение.
% 5. МОДЕЛИРОВАНИЕ ЛОГИЧЕСКОГО ПРОТИВОРЕЧИЯ
% ... (код создания матрицы решений с противоречием на диагонали) ...
imagesc(program_space, program_space, results);
hold on;
plot(program_space, program_space, 'k-', 'LineWidth', 3); % Диагональ
title('Матрица решений оракула H', 'FontSize', 12);
subplot(1,2,2);
plot(program_space, diagonal, 'b-o', 'LineWidth', 2); % Фактический результат
plot(program_space, program_space, 'r--', 'LineWidth', 2); % Ожидание
plot(program_space(idx), diagonal(idx), 'ro', 'MarkerSize', 15); % Точка P(P)
title('Парадокс на диагонали самореференции', 'FontSize', 12);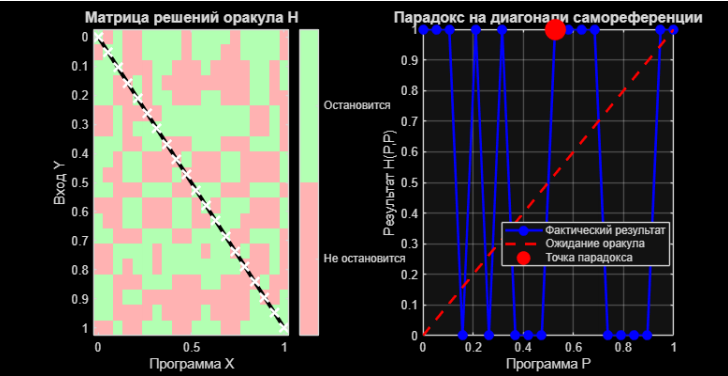
Примечание : Рис. 2: Слева — матрица решений гипотетического оракула. Диагональ, где программа анализирует саму себя, — это место потенциального сбоя. Справа — график этого сбоя: поведение P(P) (красная точка) не может лежать ни на красной (ожидание остановки), ни быть согласовано с синей линией (реальные результаты), демонстрируя разрыв.
Финал нашей визуальной демонстрации — «логический взрыв» (Рис. 3). Мы представляем парадокс как волну, расходящуюся из эпицентра — точки P(P). Эта красивая, симметричная, но внутренне противоречивая структура — символ того, как одно-единственное противоречие разрушает стройное здание гипотезы о существовании H. Взрыв не физический, а концептуальный: взрыв невозможности.
% 6. ФИНАЛЬНАЯ ДЕМОНСТРАЦИЯ ЛОГИЧЕСКОГО ВЗРЫВА
figure('Position', [100 100 600 600]);
% ... (код создания волновой поверхности "взрыва") ...
surf(X_ex, Y_ex, Z_explosion, 'EdgeColor', 'none', 'FaceAlpha', 0.9);
plot3(0, 0, max(Z_explosion(:)), 'ro', 'MarkerSize', 20); % Эпицентр
title('ЛОГИЧЕСКИЙ ВЗРЫВ', 'FontSize', 16, 'FontWeight', 'bold');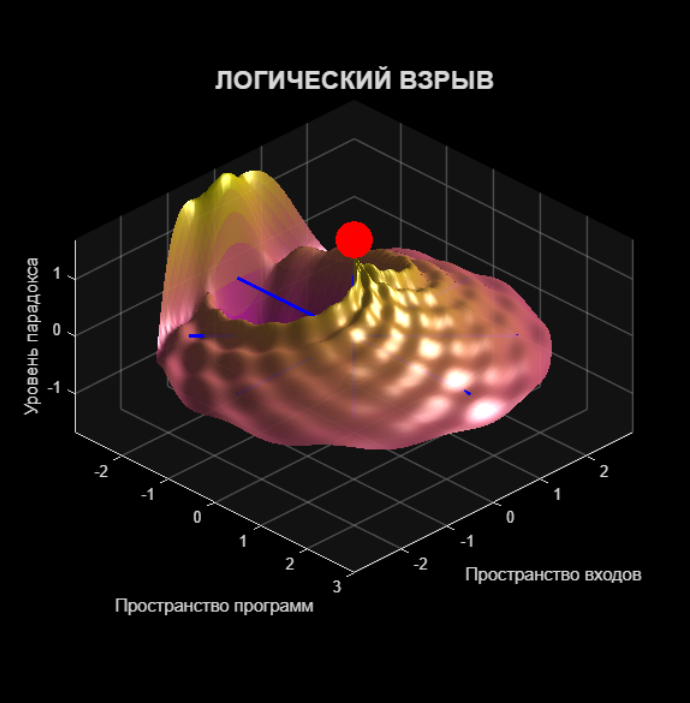
H. Эпицентр — точка P(P). Наш MATLAB-эксперимент не создал оракула — он смоделировал его крах. Мы прошли весь путь доказательства Тьюринга в наглядной форме:
-
Предположили существование
Hи визуализировали его как идеальный классификатор. -
Сконструировали программу
P, чья логика материализовалась в виде фрактальной сложности и четкой условной схемы. -
Применили самореференцию (
P(P)), что на графиках отобразилось как точка на диагонали. -
Обнаружили логический разрыв: в этой точке любое решение
Hведет к обратному поведениюP. Вектора на графике разошлись, кривая на диагонали разорвалась. -
Визуализировали итог как «взрыв» — распространяющуюся из точки противоречия несовместимость.
Финальный итог терминала :
==========================================
ДОКАЗАТЕЛЬСТВО ЗАВЕРШЕНО
Анализ показывает:
1. Предположим существование оракула H
2. Построим программу-провокатор P
3. Рассмотрим вычисление P(P)
4. Получаем логическое противоречие:
- Если H(P,P)=1, то P(P) зацикливается
- Если H(P,P)=0, то P(P) останавливается
5. Следовательно, H не может существовать
ВЫВОД: Проблема остановки алгоритмически неразрешима.
==========================================Таким образом, наше моделирование — не попытка решить неразрешимое, а мощный инструмент для понимания сути этого фундаментального ограничения. Мы не смогли построить , но мы смогли увидеть и показать, почему это невозможно. Графики и код превратили абстрактный парадокс в зримую драму вычислений, где логика, обращенная на себя, неизбежно приводит к взрыву. Это и есть живое, экспериментальное подтверждение теоремы Тьюринга.
Доказательство неразрешимости проблемы остановки — не просто красивая головоломка для математиков. Это фундаментальный результат, который провел четкую границу между тем, что можно и нельзя узнать с помощью алгоритмов. Он поставил пределы самому человеческому познанию в той его части, что опирается на вычисления и формальную логику.
Теперь мы проведем 4 границы познания :
Для программирования: Вечная война с неопределенностью
Мечта о «идеальном отладчике», который одним взглядом на код находит все ошибки [7], разбилась о доказательство Тьюринга.
-
Статический анализ обречен на несовершенство. Современные инструменты анализа кода — это не оракулы. Они ищут известные шаблоны уязвимостей и антипаттерны. Однако проблема остановки доказывает: не существует алгоритма, который гарантированно на��дет все потенциальные бесконечные циклы или логические тупики. Всегда останутся программы, чье поведение анализатор не сможет предсказать, не запустив их. Это фундаментальная «слепая зона», которую нельзя устранить — можно лишь сузить, увеличивая сложность эвристик.
-
Верификация программ имеет пределы. Формальные методы доказательства корректности программ (как в критическом ПО для авиации или медицины) — мощный инструмент. Но они работают для конкретных программ и спецификаций. Теорема Тьюринга говорит: нельзя создать универсальную систему верификации, которая докажет правильность любой произвольной программы. Для каждой новой сложной системы доказательство нужно выстраивать заново, и для некоторых систем оно может оказаться невозможным в рамках заданной формальной логики.
Практический вывод для разработчика: Примите неопределенность как данность. Ваши инструменты — умные, но не всемогущие. Любой статический анализ — это вероятностная оценка, а не абсолютный приговор. Полная уверенность в поведении произвольного кода алгоритмически недостижима.
Для математики: Эхо теоремы Гёделя
В 1931 году Курт Гёдель доказал свою знаменитую теорему о неполноте: в любой достаточно мощной формальной системе (как арифметика) существуют истинные утверждения, которые нельзя доказать средствами самой этой системы.
Работа Тьюринга 1936 года стала вычислительным переложением этой идеи. Покажите, что:
-
Проблема остановки неразрешима.
-
Любое математическое утверждение можно закодировать как вопрос об остановке некой специально построенной программы (которая ищет контрпример к утверждению).
-
Следовательно, если бы мы могли алгоритмически доказывать все истинные утверждения (т.е. решать проблему остановки для этих программ-искателей), мы бы нарушили теорему Гёделя.
Таким образом, неразрешимость проблемы остановки — это вычислительный аналог неполноты. Она показывает, что «истина» и «доказуемость» — разные вещи, и между ними лежит пропасть, которую не может перекрыть ни один конечный алгоритм. Математика, как и программирование, обречена на незавершенность.
Для Computer Science: Карта территории невозможного
Проблема остановки стала прототипом, открывшим целый класс алгоритмически неразрешимых проблем. Если некая задача может быть «сведена» к проблеме остановки (то есть её решение позволило бы решить и проблему остановки), то и она сама неразрешима. Это мощный инструмент для определения границ вычислимости.
-
Проблема соответствия Поста (Post Correspondence Problem): Простая игра со строками, которая кажется головоломкой, но оказывается столь же неразрешимой, как и проблема остановки. Невозможно создать алгоритм, который для произвольного набора карточек со словами определит, можно ли из них составить две одинаковые последовательности.
-
Проблема эквивалентности программ: Не существует алгоритма, который для двух произвольных программ определит, вычисляют ли они одну и ту же функцию для всех входных данных.
-
Проблема проверки на вирус: В общем случае невозможно создать антивирус, который без ложных срабатываний и пропусков определит, содержит ли произвольная программа вредоносный код (поскольку это сводится к анализу её бесконечного поведения).
В итоге теория вычислимости не просто говорит, что «сложно», она указывает на задачи, которые в принципе не имеют алгоритмического решения. Это позволяет ученым и инженерам не тратить силы на поиск невозможного, а фокусироваться на поиске приближенных решений или на подклассах задач, которые всё же разрешимы.
Для будущего ИИ: Фундаментальный барьер для «всеведения»
Мечты о создании сверхразума, способного ответить на любой вопрос, наталкиваются на доказательство Тьюринга.
-
ИИ как вычислительная система: Любой искусственный интеллект, реализованный на классическом компьютере (включая современные нейросети), по определению является вычислимой функцией — программой. А значит, на него распространяются все ограничения, выведенные Тьюрингом.
-
Оракул для ИИ: Представьте «всезнающий» ИИ как оракул
H. Мы могли бы построить для него программу-провокаторP_AI, которая задает ему вопрос: «Завершится ли твой собственный мыслительный процесс при анализе этого вопроса?» — и поступает наоборот. Это приводит к тому же парадоксу. Не существует вычислимой системы (ИИ), которая могла бы безошибочно предсказать результат своей собственной работы для всех возможных входных данных. -
Пределы самопознания и предсказания: Это накладывает фундаментальное ограничение на способность ИИ к полному самопониманию и предсказанию последствий своих действий в произвольных сложных ситуациях. Будут всегда существовать вопросы (особенно мета-вопросы о нем самом и его взаимодействии со средой), на которые даже сверхразумный, но конечный алгоритм не сможет дать однозначного ответа.
Итог для философии ИИ: Мы не сможем создать бога в машине. Мы сможем создать невероятно могущественные, но принципиально ограниченные инструменты. Их сила будет не во «всеведении», а в способности решать колоссальное, но всё же ограниченное подмножество задач из области человеческих интересов. Проблема остановки — это напоминание, что даже в эпоху ИИ непознаваемое останется частью нашей реальности.
Таким образом, результат Тьюринга — это не тупик, а карта. Он четко очертил континент того, что подвластно алгоритмам, и указал на океан невозможного, который его окружает. Понимание этих границ — не поражение, а высшая форма знания. Оно освобождает нас от погони за химерами и позволяет сфокусировать гений [8] человеческой мысли на том, что действительно достижимо, делая наши технологии не менее могущественными, но гораздо более осознанными.
В конце хочу сказать , что проблема остановки и её доказательство — это не история о том, чего мы не можем. Это история о том, что мы узнали. Узнали фундаментальную истину о природе вычислений, логики и самого познания. Неразрешимость — это не поражение разума, а его триумф: карта, на которой четко, математически безупречно, очерчены границы территории, доступной алгоритмам. Это освобождающее знание. Оно останавливает бесплодные поиски абсолютного, всемогущего инструмента и направляет творческую энергию в плодотворное русло — на изучение и освоение обширного континента разрешимого.
Машина Тьюринга, начавшаяся как абстрактная модель механического вычисления, и простая программа-провокатор , построенная из чистого логического противоречия, стали краеугольными камнями, на которых стоит вся современная computer science. Они превратили её из набора инженерных решений в глубокую, философски насыщенную дисциплину, задающую вопросы о пределах знания, природе разума и структуре реальности, которую можно описать алгоритмом. Понимание, что в сердце цифрового мира лежит принципиально неразрешимая проблема, заставляет нас смотреть на технологии не как на магию, а как на мощный, но ограниченный инструмент, чьи возможности и границы мы теперь понимаем изнутри.
Какие дальнейшие горизонты и практические выводы из этого следуют ?
Глубже в теорию: Тьюринг, Гёдель и сны о формализации
Элегантность доказательства Тьюринга оттеняется его глубокой связью с теоремой Гёделя о неполноте (1931). Гёдель показал, что в любой достаточно богатой математической системе существуют истинные утверждения, недоказуемые в её рамках. Тьюринг, по сути, дал этому феномену вычислительную интерпретацию. Можно представить программу, которая последовательно перебирает все возможные доказательства в формальной системе в поисках доказательства противоречия. Вопрос «остановится ли эта программа?» эквивалентен вопросу «непротиворечива ли система?». Неразрешимость первого вопроса делает алгоритмически неразрешимым и второе. Таким образом, мечта Гильберта о полной, непротиворечивой и завершаемой формализации всей математики была разрушена вдвойне: сначала метаматематически Гёделем, затем — алгоритмически Тьюрингом.
Другие «неразрешимые» монстры: Проблема соответствия Поста
Проблема остановки стала родоначальницей целого зоопарка неразрешимых проблем. Один из самых изящных и наглядных «монстров» — Проблема соответствия Поста (ПСП). Её формулировка проста до гениальности: дан набор карточек, на каждой из которых написано два слова (например, ). Можно ли выбрать последовательность этих карточек (с повторами) так, чтобы верхняя и нижняя склейки слов совпали? Оказывается, не существует общего алгоритма, отвечающего на этот вопрос для произвольного набора. Это проблема не о поведении программ во времени, а о статическом свойстве строк — и она столь же неразрешима. ПСП — мощный инструмент для доказательства неразрешимости других задач, особенно в теории формальных языков и лингвистике.
Таким образом, осознание абсолютного предела — проблемы остановки — становится источником практической мудрости и двигателем прогресса. Оно учит нас скромности перед лицом сложности, направляет наши усилия на достижимое и делает нас лучше как инженеров, ученых и мыслителей, создающих технологии в мире, где всемогущие алгоритмы невозможны, но невероятно мощные — уже реальность.
Автор: DigitalPsychiatry
Источник [9]
Сайт-источник BrainTools: https://www.braintools.ru
Путь до страницы источника: https://www.braintools.ru/article/23877
URLs in this post:
[1] парадоксе: http://www.braintools.ru/article/8221
[2] логику: http://www.braintools.ru/article/7640
[3] интеллекта: http://www.braintools.ru/article/7605
[4] математику: http://www.braintools.ru/article/7620
[5] поведение: http://www.braintools.ru/article/9372
[6] поведение: http://www.braintools.ru/article/5593
[7] ошибки: http://www.braintools.ru/article/4192
[8] гений: http://www.braintools.ru/article/4566
[9] Источник: https://habr.com/ru/articles/981908/?utm_source=habrahabr&utm_medium=rss&utm_campaign=981908
Нажмите здесь для печати.