Гиперсети: нейронные сети для обработки иерархических данных

С точки зрения нейронных сетей мир плоский. Иерархические данные напоминают, что это не так.

Работа нейронных сетей неотделима от допущения, что всего одна функция отображает вводные данные на выходные. Но в реальных условиях данные редко вписываются в такие рамки.

Допустим, есть клиническое исследование, проводимое сразу в нескольких больницах. Лекарство одно и то же, но отличаются популяции пациентов, процедуры и порядок ведения записей. В таких случаях наблюдения группируются в разные датасеты, каждый из которых управляется скрытыми параметрами.

Стандартные нейронные сети в таких условиях жёстко сбоят. Обучите одну модель сразу на всех датасетах — и она расфокусируется из-за различий, станет усреднять функции, которые усреднять не следует. Натренируйте по модели на каждом из датасетов — и получите переобучение, в особенности, если датасеты будут маленькими. Такие обходные манёвры как задействовать статические векторные представления (эмбеддинги) или постоянно наращивать размер сети в сущности не решают ключевую проблему: система запоминает причуды сети, не моделируя её структуру, складывающуюся на уровне датасета. А ведь именно эта структура — залог качественных результатов.

В этом посте мы проанализируем иной подход, а именно создание гиперсетей. С их помощью можно научить нейронные сети адаптироваться к датасету. Гиперсеть не будет заучивать одно фиксированное отображение, а освоит генерацию параметров другой сети на основании датасета, полученного в качестве эмбеддинга. В результате получится модель, способная:

• На основании всего пары точек данных выводить свойства, действующие на уровне всего датасета,

• Адаптироваться к совершенно новым датасетам без повторного обучения и

• Аккумулировать информацию, взятую из разных датасетов, для повышения стабильности и купирования переобучения.

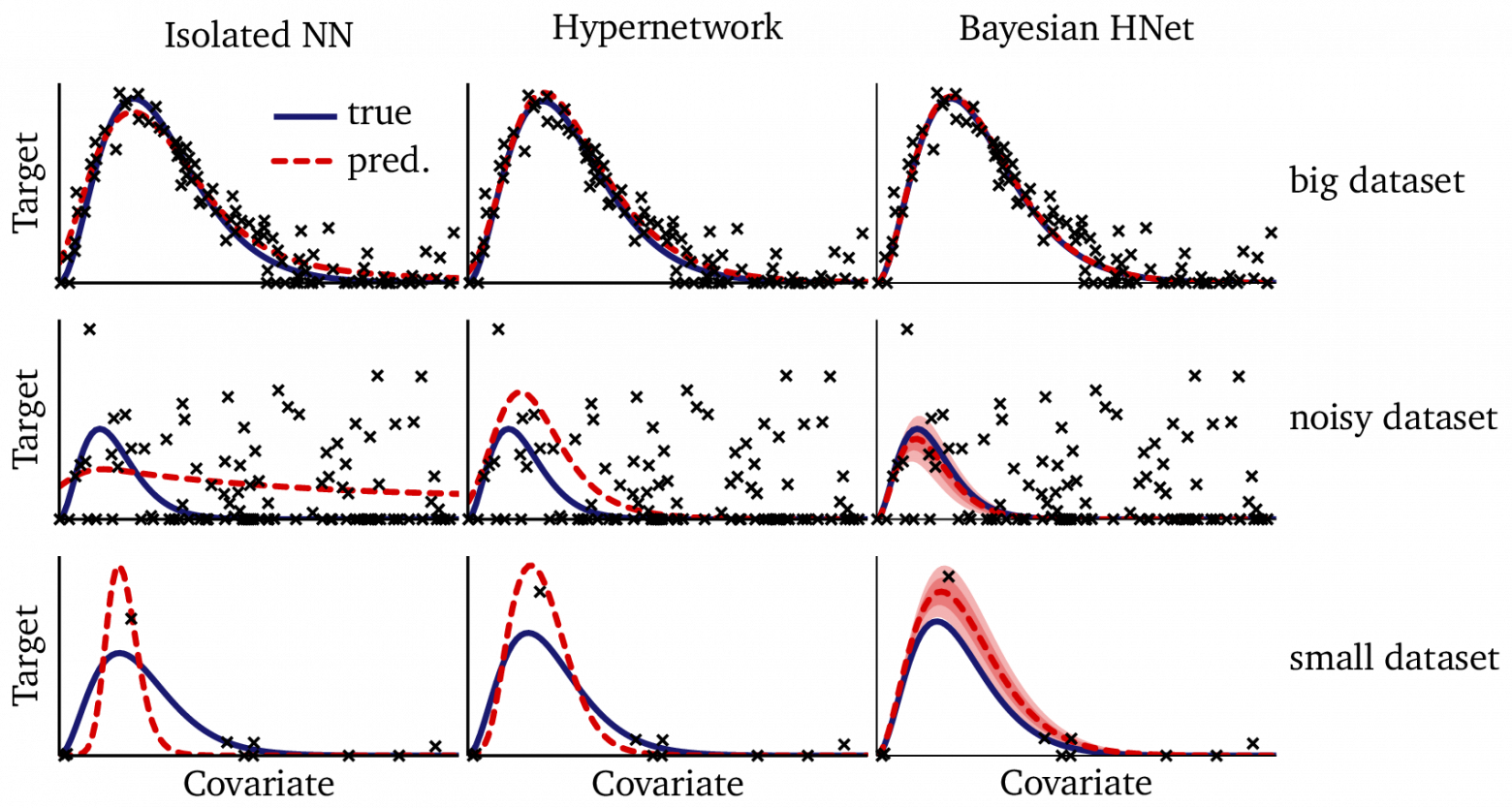
В этой статье мы пошагово построим модель. К ней прилагается код, который вы сами можете выполнить и протестировать на синтетических данных, сгенерированных на базе закона Планка. Изучая эту тему, мы также сравним гиперсети с традиционными нейронными сетями и приоткроем тайну, почему в некоторых случаях байесовские модели могут справляться даже лучше.

1. Введение

При решении многих реалистичных задач приходится работать с данными, которые иерархичны по своей природе: результаты наблюдений группируются во взаимосвязанные, но разные датасеты, каждым из которых управляют присущие ему скрытые свойства. В качестве примера возьмём клиническое исследование, в рамках которого тестируется новый препарат. В исследовании участвует множество больниц, и в ходе работы фиксируется, в какой дозировке получал препарат каждый пациент плюс данные о том, как это повлияло на пациента. Естественно, главным фактором, определяющим итоги исследования, является эффективность препарата. Но определённую роль играют и условия, характерные для каждой больницы. Демографические данные о пациентах, процедурные отличия и даже способ фиксации результатов также могут привести к коррекции итогового результата. Если эти отличия существенны, то нельзя трактовать данные как поступившие всего от одной популяции, поскольку это приведёт к неверным выводам об эффективности препарата.

С точки зрения машинного обучения конфигурация очень непростая. Свойства, действующие на уровне датасетов — а именно, как результаты варьируются от больницы к больнице — неявные: они существуют, но прямо не наблюдаются. Стандартная нейронная сеть выучит ровно одно постоянное соответствие между некоторыми входными и некоторыми выходными данными, но именно здесь это соответствие является неоднозначным. Две разных больницы, в которых отличаются неявные условия, дадут разные результаты даже для пациентов с идентичными профилями. Функция становится вполне определённой (то есть, однозначной), только когда в ней учтены факторы, действующие на уровне отдельных датасетов.

Чтобы конкретизировать эти выкладки, составим упрощённый пример, на котором попробуем количественно выразить интересующие нас показатели исследования. Каждый датасет будет состоять из наблюдений (𝝂, y), выведенных из простой иерархически структурированной функции. Функцию мы сгенерируем по закону Планка:

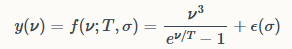
где:

• 𝝂 — это ковариата (частота),

• y — это отклик (яркость или поток),

• T — это параметр, специфичный для датасета (температура). В рамках данного датасета этот параметр является постоянным, но от датасета к датасету может варьироваться; наконец

• ε — это гауссовский шум с масштабным фактором σ, который остаётся неизвестным, но во всех датасетах является одинаковым.

На основе этих данных можно было бы отобразить пиксели на картинке, визуализирующей температуру. Каждый пиксель на картинке «обладает» собственной поверхностной температурой T, от которой зависит её спектр, тогда как масштаб шума σ — это свойство спектрографа или усилителя, которое остаётся согласованным во всём разбросе наблюдений.

В данном случае самое важное, что, тогда как моделирующий человек наблюдает и знает пары (𝝂, y), параметр T входит в состав функции, генерирующей данные, и наблюдателю он не известен. Притом, что функция f(𝝂; T) является постоянной (каждый из датасетов укладывается в одно и то же общее уравнение), у каждого датасета свой особый T, поэтому отображение y(𝝂) от датасета к датасету варьируется. Такая фундаментальная структура — содержащая специфичные для каждого датасета скрытые переменные, которые влияют на наблюдаемые соответствия — повсеместно встречается в реалистичных задачах.

Если поступить бесхитростно и обучить одну модель сразу на всех датасетах, то тем самым мы принудим сеть проигнорировать эти латентные отличия и аппроксимировать «среднюю» функцию. Такой подход фундаментально не подходит для работы с неоднородными (гетерогенными) данными. Подгонять модель под каждый датасет — также не выход. Если датасет маленький, то точек данных в нём просто не хватит, чтобы модель уверенно научилась. Кроме того, разделяемая функциональная структура вместе с разделяемыми параметрами, такими, как масштабный фактор шума σ, не поддаётся надёжной оценке, если не прибегать к пулингу информации.

Напротив, именно для таких случаев нам потребуется иерархическая модель — такая, в которой одновременно учитывалась бы вариативность, специфичная для отдельных датасетов, а также был налажен обмен информацией между датасетами. При использовании нейронных сетей этот путь логично приводит нас к метаобучению: получаются модели, не просто изучающие функцию, но и научающиеся, как следует изучать функции.

Вывод

Работа стандартных нейронных сетей основана на допущении, что одна функция может охватить все данные. Но (очень распространённые) иерархические данные фундаментально не соответствуют этому допущению. Нужны такие модели, которые при необходимости могли бы адаптироваться к каждому датасету, но при этом продолжали совместно пользоваться информацией, которая согласуется в разных датасетах.

2. Почему стандартные нейронные сети не справляются с иерархическими данными

Стандартная нейронная сеть, обученная непосредственно на парах (𝝂, y), в вышеописанной конфигурации сбоит из-за допущения, будто существует одна универсальная функция, способная соотнести вводные значения с выходными сразу во всех латасетах. Но в сформулированной нами задаче каждый датасет подчиняется своей функции y(𝝂), зависящей от скрытого параметра T, специфичного для конкретного датасета. Мы не располагаем однозначной функцией f(𝝂; T), поскольку мы не можем наблюдать параметр T. Без явного доступа к T нейронная сеть не может знать, каким именно отображением пользоваться.

Неоднозначные отображения

Чтобы было понятнее, в чём здесь проблема, давайте попробуем спрогнозировать рост человека, не опираясь ни на какую дополнительную информацию. В однородной популяции — скажем, где присутствуют только взрослые — обычное среднее значение будет достаточно хорошим прогнозом. Например, если рассматриваемая популяция — это взрослые голландки, то среднее значение в 68% процентов случаев будет соответствовать фактическому росту женщины с погрешностью ± 5 сантиметров. Но допустим, что в набор входят данные как по взрослым, так и по детям. Если распределение всего одно, то модель неизбежно выучит «средний» рост, который не будет адекватен ни для детей, ни для взрослых. Прогнозы с таким использованием среднего практически никогда не бывают правильными.

Аналогичная проблема возникает и в нашей иерархической ситуации: поскольку нет такой функции, которая одновременно охватывала бы все датасеты, не слишком адекватны будут прогнозы, сделанные на основе «средней» функции.

Обычные обходные маневры, и почему их недостаточно

• Статические эмбеддинги в датасете: зачастую пытаются присвоить каждому датасету уникальное векторное представление (эмбеддинг), извлекаемое из таблицы поиска. Благодаря этому сеть запоминает, какие корректировки соответствуют каждому конкретному датасету. Но эта стратегия не обобщается: поступает новый датасет, и у сети нет векторного представления для него, поэтому она и не может адаптироваться к работе с новым датасетом.

• Обучение по короткому пути (shortcut learning): другой вариант — просто увеличить сеть и наполнить её дополнительными данными. В принципе, модель может улавливать тонкие статистические подсказки — отличия в паттернах шума или распределениях ввода — которые косвенно кодируют индекс датасета. Но такое «обучение по короткому пути» получается одновременно неэффективным и ненадёжным. Сеть запоминает причуды, присущие конкретным датасетам, а не делает то, что нужно — то есть, не моделирует в явном виде отличия, возникающие на уровне датасетов. В прикладных областях из‑за этого возникает сдвиг: например, сеть может научиться неверно использовать прокси‑переменную (такую как почтовый код или демографические данные), из‑за чего будут возникать нечестные или нестабильные прогнозы.

Что нам нужно на самом деле

Эти недостатки помогают понять, какие требования к модели иерархических данных действительно актуальны. Мы не вынуждаем единственную сеть одновременно аппроксимировать каждый из датасетов, просто нам нужна модель, которая может:

• На основе немногочисленных примеров выводить свойства, применимые ко всему датасету,

• Адаптироваться к совершенно новым датасетам без повторного обучения с нуля и

• Эффективно аккумулировать данные из разных датасетов, так, чтобы надёжнее оценивались совместно используемая структура (например, функциональная форма или масштабный фактор шума σ).

Стандартные нейронные сети, обладающие фиксированной структурой, просто не способны удовлетворить эти требования. Чтобы продвинуться далее, нам требуется модель, которая динамически адаптируется к специфической структуре датасета, но при этом продолжает учиться на данных, вытянутых из разных датасетов. Гиперсети — это интересная попытка подступиться к данной проблеме.

Вывод

Такие ухищрения, как применение статических векторных представлений или укрупнение моделей не решают ключевую проблему: из-за факторов, скрытых в датасете, отображения с входных данных на выходные получаются многозначными. Нейронная сеть, функция которой по определению результирует в одно значение, не может охватить такие данные. Требуется модель, которая (1) выводит свойства сразу из всего датасета, (2) адаптируется к новым датасетам и (3) аккумулирует знания, подтянутые из разных датасетов.

3. Нейронные сети адаптируются к датасету

3.1 Векторные представления датасетов

Создавая сеть, адаптирующуюся к датасету, нужно первым делом обеспечить модели способ представлять вариабельность на уровне датасета. Для этого введём векторное представление датасета: латентный вектор E, резюмирующий свойства датасета в целом.

Каждому учебному датасету присвоим доступное для изучения учебное представление:

# векторные представления датасета (инициализированные случайными значениями и обновляемые в процессе обучения)
dataset_embeddings = tf.Variable(
    tf.random.normal([num_datasets, embed_dim]),
    trainable=True
)

# Присваиваем индексы датасета каждой выборке
dataset_indices = np.hstack([np.repeat(i, len(v)) for i, v in enumerate(vs)])
x_train = np.hstack(vs).reshape((-1, 1))
y_train = np.hstack(ys).reshape((-1, 1))

# Извлекаем векторные представления, специфичные для датасета 
E_train = tf.gather(dataset_embeddings, dataset_indices)

На первый взгляд код может напомнить обычный поиск по векторным представлениям. В такой ситуации каждому датасету присваивается статический вектор, извлекаемый из таблицы — но выше мы уже подробно обсудили, почему в данном случае такой подход не сработает!

В ходе обучения эти векторные представления в самом деле действуют как стандартные векторные представления (и реализованы именно так). Наши векторные представления, как и стандартные, нужны для кодирования свойств, специфичных для датасета. Ключевое отличие здесь заключается в том, как именно мы обращаемся с векторными представлениями на этапе логического вывода: на векторных представлениях можно продолжать учиться, даже в период прогнозирования. Если во время логического вывода поступает датасет, который модель ранее не видела, то мы инициализируем для этого датасета новые векторные представления и оптимизируем его на лету. В результате векторное представление превращается в функцию самого датасета, а не в жёстко закодированный (и, следовательно, константный) идентификатор. В ходе тренировки модель изучает векторные представления, в которых схвачены факторы, скрытые в процессе генерации данных (например, применительно к нашей задаче — параметр T). Векторное представление продолжает адаптацию и на этапе прогнозирования, благодаря чему модель может представлять новые датасеты, которых она ранее не видела. Такая гибкость критически важна для обобщения данных.

3.2 Знакомство с гиперсетью

Когда векторные представления датасетов готовы, нам требуется механизм, позволяющий транслировать эти векторные представления в значимые изменения в поведении сети. Наиболее естественно сделать это при помощи гиперсети: вторичной нейронной сети, которая генерирует параметры для главной сети.

Это одновременно простая и мощная идея. Мы изучаем не отдельную функцию f(𝝂), а семейство функций f(𝝂; E), параметризованных векторным представлением датасета E. Гиперсеть принимает E на вход и производит веса и смещения для первого слоя главной сети. В таком случае от информации, специфичной для датасета, непосредственно зависит, как главная сеть будет обрабатывать поступающие на вход данные. Остальная часть сети, не считая первого слоя, работает независимо от датасета. Фактически, мы вынесли семейство функций  f(𝝂; E) в композицию g(𝝂; h(E)), и наша задача — изучить функции g и h, которые аппроксимируют наш процесс генерации данных.

Вот минимальная реализация средствами Keras:

def build_hypernetwork(embed_dim):
    """Генерация параметров для первого слоя главной сети"""

    emb = K.Input(shape=(embed_dim,), name='dataset_embedding_input')

    l = K.layers.Dense(16, activation='mish', name='Hyper_L1')(emb)
    l = K.layers.Dense(32, activation='mish', name='Hyper_L2')(l)

    # Генерация весов слоя (32 скрытых единицы, 1 входной признак)
    W = K.layers.Dense(32, activation=None, name='Hyper_W')(l)
    W = K.layers.Reshape((32, 1))(W)  # Reshape to (32, 1)

    # Генерация смещений (32 скрытых единицы)
    b = K.layers.Dense(32, activation=None, name='Hyper_b')(l)

    return K.Model(inputs=emb, outputs=[W, b], name="HyperNetwork")

Гиперсеть преобразует векторное представление датасета в набор параметров слоёв (W, b). Эти параметры заменят фиксированные веса, присутствующие в первом слое главной сети, в результате чего вводные данные будут преобразованы в соответствии со спецификой датасета, и на полученном результате можно будет учиться.

Гиперсеть отображает векторные представления датасетов на параметры нейронной сети. Таким образом напрямую схватывается вариабельность, существующая на уровне датасета, так, что каждый датасет моделируется собственной эффективной функцией, поэтому нам не требуется обучать отдельные сети с нуля. Примечательно, что, при всей этой гибкости, все параметры гиперсети остаются постоянными относительно датасета. Та специфичная для датасета информация, которая нам потребуется, чтобы добиться такой гибкости — это лишь одно векторное представление (в нашем случае — 4 числа с плавающей точкой на датасет).

3.3 Интеграция с главной сетью

Итак, теперь у нас есть гиперсеть, чтобы генерировать параметры, специфичные для датасета, и на следующем шаге мы должны интегрировать эти параметры в главную сеть, моделирующую данные. Главная сеть может иметь любую угодную нам архитектуру; всё, что требуется сделать — заменить первое фиксированное линейное преобразование преобразованием, специфичным для датасета и выводимым из векторного представления.

Для этого можно определить пользовательский слой, который будет применять сгенерированные гиперсетью веса и смещения:

class DatasetSpecificLayer(K.layers.Layer):

    def __init__(self, **kwargs):
        super(DatasetSpecificLayer, self).__init__(**kwargs)

    def call(self, inputs):
        """ Применяет преобразование, специфичное для датасета, пользуясь сгенерированными весами """

        x, W, b = inputs  # unpack inputs

        x = tf.expand_dims(x, axis=-1)       # Форма: (batch_size, 1, 1)
        W = tf.transpose(W, perm=[0, 2, 1])  # Транспонирование W в (batch_size, 1, 32)

        out = tf.matmul(x, W)          # Форма: (batch_size, 1, 32)
        out = tf.squeeze(out, axis=1)  # Форма: (batch_size, 32)

        return out + b  # Добавим смещение, окончательная форма: (batch_size, 32)

Этот слой служит мостиком между гиперсетью и главной сетью. Мы не полагаемся на единственный фиксированный набор весов; напротив, преобразование, применяемое к каждому входному образцу, подстраивается под датасет через его векторное представление.

Обустроив этот компонент, можно определить главную сеть:

embed_dim = 4
hypernet = build_hypernetwork(embed_dim)

def build_base_network(hypernet, embed_dim):
    """ Главная сеть, принимающая на вход x и векторное представление датасета """

    inp_x = K.Input(shape=(1,), name='input_x')
    inp_E = K.Input(shape=(embed_dim,), name='dataset_embedding')

    # Получаем от гиперсети специфичные для датасета веса и смещения 
    W, b = hypernet(inp_E)

    # На основании сгенерированных весов получаем пользовательский слой 
    l = DatasetSpecificLayer(name='DatasetSpecific')([inp_x, W, b])

    # Продолжаем работать с нормальной плотной сетью 
    l = K.layers.Activation(K.activations.mish, name='L1')(l)
    l = K.layers.Dense(32, activation='mish', name='L2')(l)
    l = K.layers.Dense(32, activation='mish', name='L3')(l)
    out = K.layers.Dense(1, activation='exponential', name='output')(l)

    return K.Model(inputs=[inp_x, inp_E], outputs=out, name="BaseNetwork")

Почему в последнем слое применяется экспоненциальная активация? Результаты расчётов по закону Планка строго положительные, и большим x соответствуют exp(-x). Следовательно, этот выбор отражает предвосхищаемое нами решение и располагает к тому, чтобы примерно линейный вывод от активации функции Миша в слое L3 естественным образом превращался в экспоненциальный хвост. Мы пришли к такому варианту, исходя из физики датасета и обнаружили, что такой вариант обеспечивает более быструю сходимость модели и более качественную генерализацию. При экспоненциальных активациях могут возникать проблемы со сходимостью в случае с большими значениями по оси y, но в нашем датасете таких значений нет.

Напомню, как строится весь процесс:

• Гиперсеть генерирует параметры (W, b), специфичные для данного датасета.

• Далее DatasetSpecificLayer применяет это преобразование к входному значению 𝝂, в результате чего получается трансформированное представление 𝝂’. Если преобразование работает правильно, то в преобразованном пространстве все различные датасеты должны быть непосредственно сравнимы друг с другом.»

• Главная сеть заучивает одно универсальное отображение с преобразованных входов 𝝂’ на выходы y.

Интегрировав сгенерированные гиперсетью параметры в первый слой, мы преобразуем главную сеть в систему, автоматически адаптирующуюся к каждому датасету. Благодаря этому нам удаётся схватывать структуру, специфичную для каждого датасета, в то же время продолжая обучать одну модель на всех датасетах.

Вывод

Сочетая векторные представления датасетов с гиперсетью, можно выражать целое семейство функций f(𝝂; E) при помощи нейронной сети, основанной на однозначной функции. Для этого её нужно разложить на f(𝝂; E) = g(𝝂, h(E)), где g и h — это обычные однозначные нейронные сети. Первый слой главной сети приобретает специфику конкретного датасета, а в остальном нейронка продолжает работать как обычная сеть прямого распространения и изучает универсальное отображение на преобразованные входные значения.

4. Результаты обучения

Теперь, сшив воедино векторные представления, базовую сеть и гиперсеть, можно испытать нашу модель, проверив её на тестовой задаче. Для этого обучим её на коллекции из 20 синтетических датасетах, полученных по закону Планка так, как описано в разделе 1. У каждого датасета есть собственная температура, обозначенная как параметр T, притом, что один общий масштабный фактор шума σ совместно используется всеми датасетами.

На следующем рисунке показаны результаты обучения. В каждой из секций представлен один из датасетов, применявшихся при тестировании. В каждой секции есть:

• Сплошная синяя линия, соответствующая истинной функции, выведенной по закону Планка,

• Чёрные точки — это наблюдаемые учебные данные,

• Красная прерывистая кривая — это прогнозы, полученные на базе модели, основанной на гиперсети и

• Кривая из золотых точек — это прогнозы, полученные от обычной нейронной сети, обученной отдельно на каждом датасете.

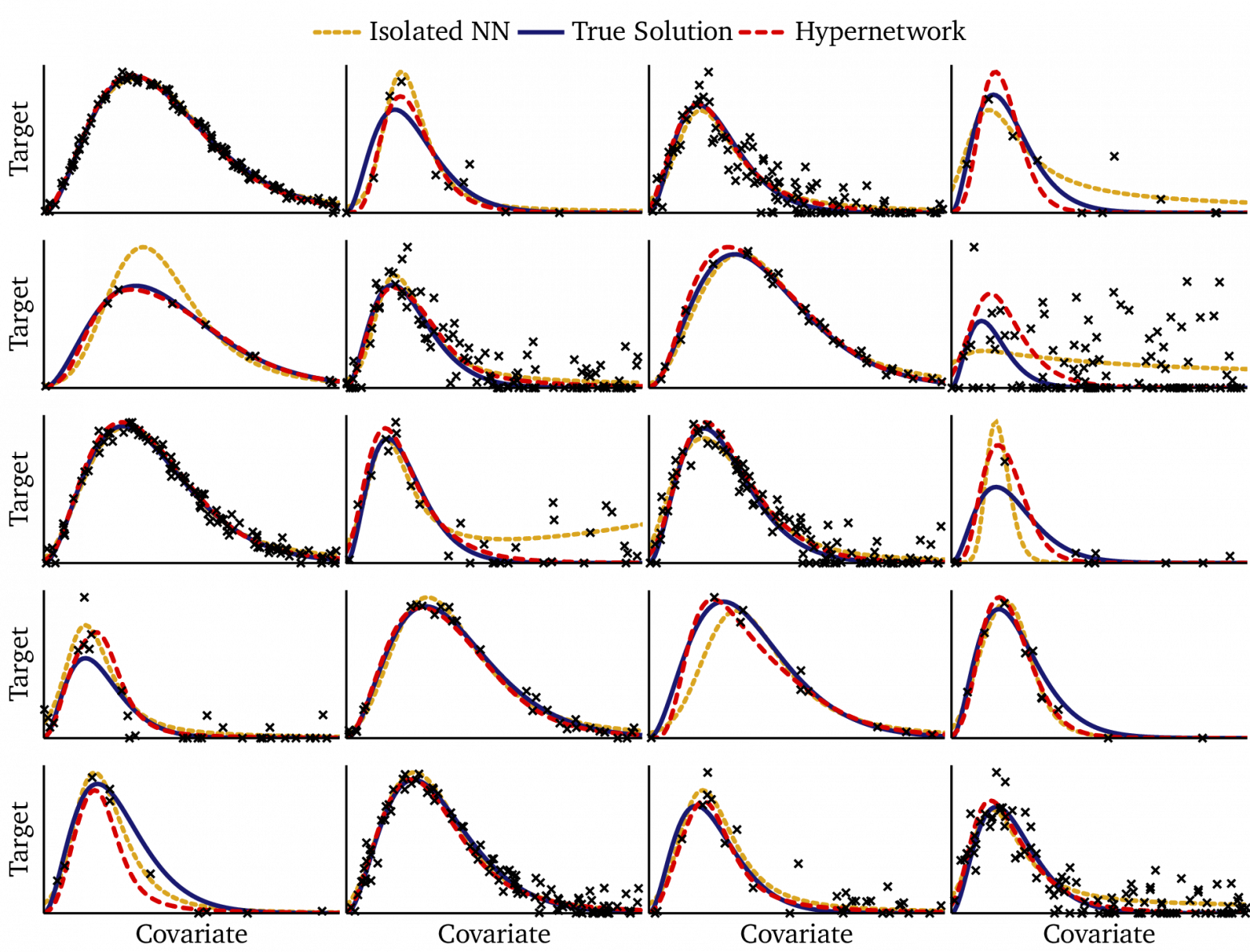
Сразу очевидно выделяются несколько паттернов:

• Сравнимая общая точность: зачастую (например, в 1^‑м столбце 1^‑й сстроки) прогнозы гиперсети (красные) очень похожи на прогнозы изолированной нейронной сети (золотые). Следовательно, несмотря на то, что мы строго ограничили модель и удалили ~95% её параметров, при совместном использовании параметров на всех датасетах даже при явном дефиците данных точность датасетов не страдает.

• Повышенная стабильность: когда учебные данные разрежены (например, как в 1^‑м столбце 2^‑й строки или в последнем столбце 3^‑й строки), гиперсеть переобучается существенно меньше, чем изолированная нейронная сеть. Её прогнозы остаются более гладкими и ближе к истинной форме функции, тогда как изолированная нейронная сеть иногда не в состоянии лечь в отдельные точки.

• Аккумулирование данных из разных датасетов: обучаясь на всех датасетах одновременно, гиперсеть научается отделять совместно используемую структуру [например, масштабный фактор шума σ или основополагающую форму функции f(𝝂; T)] от вариаций, специфичных для датасета (векторное представление E). Такое разделяемое обучение стабилизирует прогнозы во всём их спектре, но особенно наглядно просматривается в тех секциях, где данные сильно зашумлены (как в случаях с последним столбцом 2^‑й строки или со 2^‑м столбцом 3^‑й строки).

Вывод

При изобилии данных гиперсеть достигает точности, сопоставимой с точностью изолированных сетей, а когда данных мало — работает гораздо точнее изолированных сетей. Такой выигрыш достигается благодаря аккумулированию информации из разных датасетов, что позволяет сети схватывать в рамках отдельно взятой моделм как общую, так и специфичную для отдельных датасетов структуру.

5. Прогнозирование для новых датасетов

Вдохновляет, как хорошо учится наша гиперсеть. Но реальная проверка для неё — в том, насколько успешно она сможет адаптироваться к новым датасетам, которых никогда ранее не видела. В отличие от традиционной нейронной сети, которая просто применяет изученные веса к любому новому вводу, наша модель структурно заточена на распознание того, что каждый датасет следует собственной специфической функции. Чтобы делать прогнозы, она должна сначала логически вывести векторное представление датасета.

5.1 Двухэтапный процесс

Адаптация к новому датасету происходит в два этапа:

• Оптимизация векторного представления датасета E’ таким образом, чтобы это представление объясняло наблюдаемые точки.

• Использование оптимизированного векторного представления E’ с целью генерации прогнозов для новых входных данных через главную сеть.

При помощи такого двухэтапного конвейера модель, опираясь на немногочисленные наблюдения, может схватывать свойства, специфичные для конкретного датасета. Для этого не требуется повторно обучать всю сеть.

5.2 Оптимизация векторного представления

Чтобы логически вывести векторное представление датасета, считаем E’ параметром, пригодным для обучения. Мы не будем обучать все веса нейронной сети с нуля, а вместо этого станем оптимизировать лишь векторное представление датасета до тех пор, пока нейронная сеть под него не подстроится. Поскольку размерность у этого векторного представления низкая (в  данном случае, всего 4 числа с плавающей точкой), такая оптимизация эффективна, и для сходимости требуется совсем немного данных.

Это удобно реализовать при помощи модели-обёртки, в которой содержится всего одно векторное представление, далее выставляемое как переменная, на которой можно учиться:

class DatasetEmbeddingModel(K.Model):

   def __init__(self, base_net, embed_dim):
       super(DatasetEmbeddingModel, self).__init__()
       self.base_net = base_net
       self.E_new = tf.Variable(
           tf.random.normal([1, embed_dim]), trainable=True, dtype=tf.float32
       )
       # для более высокой производительности на сравнительно небольших датасетах, используем tensorflow_probability:
       # self.E_new = tfp.distributions.Normal(loc=0, scale=1).sample((1, embed_dim))


   def call(self, x):
       # Замощаем E_new в пределах размерности пакета, чтобы x совпадало с размером пакета 
       E_tiled = tf.tile(self.E_new, (tf.shape(x)[0], 1))
       return self.base_net([x, E_tiled])

   def loss(self, y_true, y_pred):
       mse_loss = K.losses.MSE(y_true, y_pred)
       reg_loss = 0.05 * tf.reduce_mean(tf.square(self.E_new))  # Регуляризация L2 на E
       return mse_loss + reg_loss

Здесь векторное представление датасета E’ инициализируется случайным образом, а затем обновляется методом градиентного спуска, чтобы минимизировать ошибку прогнозирования на наблюдаемых точках. Поскольку мы оптимизируем лишь горстку параметров, этот процесс легковесный и хорошо подходит для работы с небольшими датасетами.

Оформляя векторное представление как параметр, поддающийся обучению, модель может эффективно адаптироваться к новым датасетам. При такой стратегии не приходится заново обучать всю сеть, но при этом удаётся схватывать вариации, специфичные для конкретного датасета. Всё это необходимо для точных прогнозов.

5.3 Обобщение

Одно из наиболее выдающихся достоинств этого подхода — возможность обобщать данные из совершенно новых датасетов, опираясь на минимум данных. На практике модели зачастую достаточно для адаптации всего десяти информационных точек. Такая адаптация на немногочисленных примерах (few-shot adaptation) осуществима, поскольку гиперсеть уже изучила структурированное отображение с векторного представления датасета на параметры функции. При поступлении нового датасета требуется просто изучить его векторное представление, без тонкой настройки всех весов сети.

По сравнению с традиционными нейронными сетями, для эффективной тонкой настройки которых требуются сотни или тысячи примеров, такая адаптация на основе векторных представлений позволяет использовать данные гораздо эффективнее. При таком подходе модель обрабатывает реалистичные сценарии в тех случаях, когда непрактично собирать большие количества данных для каждого нового датасета.

5.4 Ограничения

Несмотря на эти сильные стороны, подход с гиперсетями неидеален. При интерпретации прогнозов, сделанных на датасетах, не вошедших в выборку — таких, что сгенерированы тем же методом, что и тренировочные данные, но в учебную выборку не вошедших —качество заметно деградирует, особенно на материале зашумленных или цензурированных данных, а также на очень маленьких датасетах. Это показано на следующих примерах:

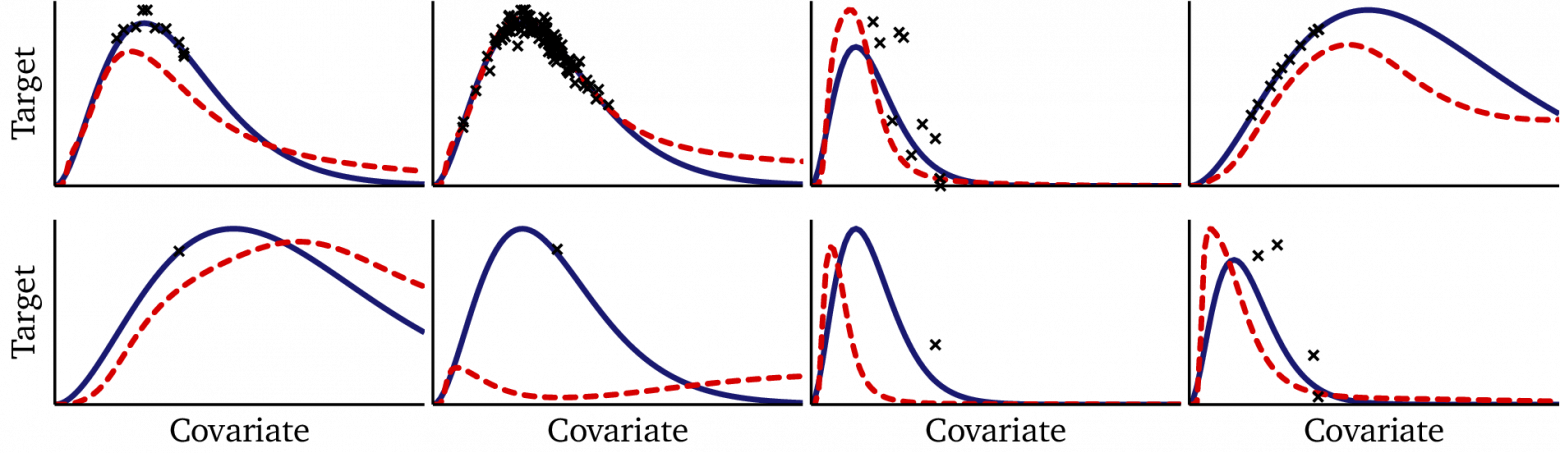
С другой стороны, это ожидаемо: исключительно сложно работать с датасетами, не вошедшими в учебную выборку, и ни одна модель машинного обучения не может гарантировать идеального обобщения на ранее не виденных данных. С другой стороны, с учётом того, какую производительность она показывала на тренировочном множестве, результаты, полученные на реальном материале, немного разочаровывают. Притом, что адаптация к конкретному датасету действительно возможна, изученные гиперсетью формы функций не всегда соблюдаются, стоит ей столкнуться с данными, не попавшими в учебный режим.  

Для обобщения данных гиперсетям достаточно всего нескольких примеров, так как мы не учим сети заново, а всего лишь адаптируем векторные представления к новым данным. Но на данных, не присутствовавших в выборке, производительность таких сетей значительно падает, поэтому для повышения надёжности нам, возможно, потребуются альтернативные подходы.

Наблюдаемая в данном случае деградация немного напоминает переобучение. Может быть, она вызвана тем этапом оптимизации, который мы прогнали в ходе логического вывода, и при какой-то другой комбинации размера шага, критериев останова, регуляризации и т.д. результаты могли бы быть лучше. Но нам такую комбинацию найти не удалось. Напротив, можно предположить, что такая деградация фундаментально обусловлена оценкой максимальной вероятности (в терминах нейронных сетей это и есть оптимизация). Оптимизация проблематична не только потому, что она проводится на этапе логического вывода, но и в принципе как алгоритм обучения.  

Вывод

Работая с новыми датасетами, мы оптимизируем лишь небольшое векторное представление E’ (на немногочисленных примерах), а не занимаемся тонкой настройкой целой сети. Гиперсеть быстро адаптируется, но может работать не очень стабильно (по сравнению с результатами, полученными на учебной выборке) на данных, примеры которых не рассматривались на этапе обучения.

6. Обсуждение и дальнейшие шаги

Гиперсетевой подход демонстрирует, как нейронные сети могут работать не только методом грубой зубрёжки, а развиваться в сторону структурированной адаптации. Задействуя векторные представления датасетов и преобразуя их при помощи гиперсети в параметры модели, мы смогли спроектировать сеть, способную логически устанавливать структуру каждого конкретного датасета, а не просто усреднять функцию на материале всех датасетов. Благодаря этому, модель может делать обобщения, опираясь на ограниченные данные — это выразительно свидетельствует об интеллектуальности системы.

Полученные нами результаты подчёркивают как сильные, так и слабые стороны этой стратегии:

Сильные стороны

• Для адаптации достаточно всего нескольких примеров: модель хорошо приспосабливается к новым датасетам, и для этого ей достаточно минимального набора наблюдений.

• Совместное обучение: благодаря аккумулированию информации из разных датасетов, повышается стабильность системы и купируется переобучение.

• Гибкая архитектура: применяя одну и ту же технику, фреймворк гиперсети можно расширять до всё более насыщенных иерархических структур.

Слабые стороны

• Снижение производительности при работе с данными, не попавшими в учебную выборку: прогнозы становятся нестабильными на материале мелких, цензурированных или зашумленных датасетов.

• Неявная структура: в векторных представлениях схватываются отличия датасетов, но без явно заданных априорных вводных модель просто не может инкорпорировать явные данные, а также плохо справляется с поддержанием единообразной формы функций.

Все эти компромиссы свидетельствуют, что гиперсети — это многообещающая, но не идеальная технология. Их можно улучшить. Например, в них недостаёт явной вероятностной структуры, необходимой для рассуждения о неопределённости и для ограничения экстраполяций. Это мотивирует нас затронуть и другое семейство моделей: байесовские иерархические сети.

При байесовских подходах мы обрабатываем иерархические данные напрямую, моделируя специфичные для датасета параметры как латентные переменные, подтянутые из уже имеющихся распределений. Когда так явно работаешь с неопределённостью, получаются более стабильные прогнозы, особенно применительно к работе с небольшими датасетами, данные из которых отсутствовали в учебной выборке.

На следующем рисунке для затравки показаны прогнозы, сделанные байесовскими моделями на тех же «внеучебных» датасетах, которые мы тестировали ранее:

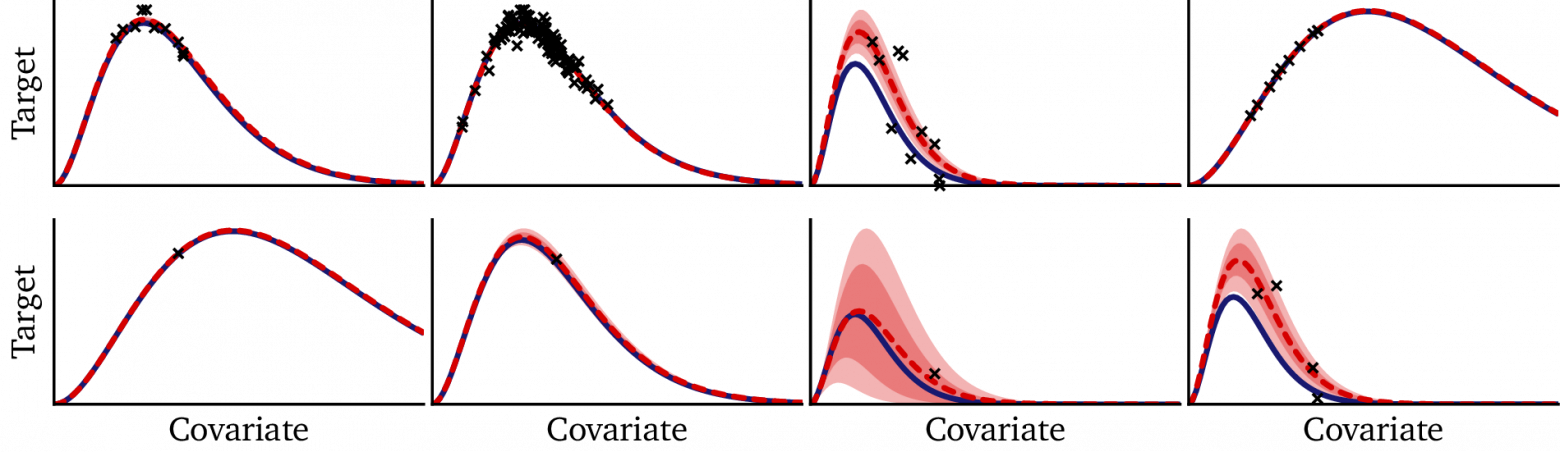
Если сравнить эти прогнозы, сделанные на внеучебных данных, с теми, что сделала гиперсеть, то результаты байесовской модели могут показаться почти волшебными!

Гиперсети привносят в иерархическое моделирование элемент метаобучения, тем самым обеспечивая гибкую и эффективную адаптацию к имеющимся данным. Но в том, что касается надёжности — особенно применительно к примерам, отсутствовавшим в учебной выборке — байесовские модели кажутся явно более выигрышными. Вместе эти модели дополняют друг друга и показывают, как приспособить машинное обучение к работе с иерархическими данными.

Вывод

Гиперсети хорошо адаптируются к структуре датасета, а для обучения им достаточно немногочисленных примеров. Но они страдают из-за отсутствия явных априорных данных и из-за того, что в них не откалибрована неопределённость.