В классическом self-attention каждый токен смотрит на другие токены, чтобы понять, что важно в данный момент.
Внимание распределяется мгновенно:
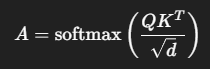
Именно этот механизм сделал трансформеры тем, чем они стали.
Но вот в чём проблема – внимание не имеет памяти.
На каждой итерации оно переобучается заново, не зная, куда оно смотрело в прошлый раз.
Из за этого внимание может скакать, шуметь и терять контекст, особенно в длинных последовательностях.
Проблема: внимание без инерции
Представьте, что вы идёте по неровной дороге.
Если вы будете менять направление мгновенно, без инерции, вас просто будет бросать из стороны в сторону.
Точно так же и внимание в трансформере:
оно то цепляется за один токен, то внезапно переключается на другой,
порождая хаотичные изменения в градиентах и мешая стабильному обучению.
А что, если добавить вниманию немного физики?
Momentum это понятие из механики.
Если у тела есть скорость, оно не останавливается мгновенно, а плавно замедляется.
Почему бы не применить тот же принцип к вниманию?
Идея:
Пусть текущее внимание немного зависит от того, каким оно было раньше.
Не только “куда я смотрю сейчас?”,
но и “куда я смотрел мгновение назад?”.
От классического внимания к Momentum Attention
В классике:
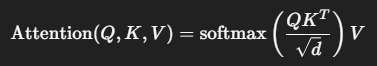
Теперь добавим инерцию к Value-векторам:
Пояснение: Если бы я добавил инерцию к attn_scores, модель была бы вынуждена смотреть на те же самые токены, что и на прошлом шаге. Это очень жесткое ограничение. Добавляя инерцию к V, я позволяю вниманию свободно выбирать, куда смотреть на каждом шаге (Q и K новые), но информация, которую оно извлекает (V), будет смесью новой и старой.
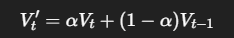
Тогда:
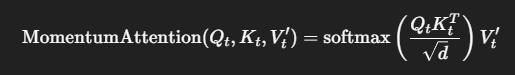
То есть текущее внимание теперь частично помнит, какие значения были важны на предыдущем шаге. α (например, 0.9) задаёт вес настоящего по сравнению с прошлым
Простой пример на pytorch
import torch
import torch.nn as nn
import torch.nn.functional as F
class MomentumAttention(nn.Module):
def __init__(self, d_model, n_heads=8, alpha=0.9):
super().__init__()
if d_model % n_heads != 0:
raise ValueError("d_model должен делиться на n_heads без остатка")
self.alpha = alpha
self.n_heads = n_heads
self.d_k = d_model // n_heads
self.W_q = nn.Linear(d_model, d_model, bias=False)
self.W_k = nn.Linear(d_model, d_model, bias=False)
self.W_v = nn.Linear(d_model, d_model, bias=False)
self.W_o = nn.Linear(d_model, d_model)
def forward(self, Q, K, V, prev_V=None):
B, T_q, D = Q.shape
_, T_k, _ = K.shape
# Линейные проекции и разделение на головы
q = self.W_q(Q).view(B, T_q, self.n_heads, self.d_k).transpose(1, 2) # [B, n_heads, T_q, d_k]
k = self.W_k(K).view(B, T_k, self.n_heads, self.d_k).transpose(1, 2) # [B, n_heads, T_k, d_k]
v = self.W_v(V).view(B, T_k, self.n_heads, self.d_k).transpose(1, 2) # [B, n_heads, T_k, d_k]
# Применение Momentum к векторам Value
if prev_V is None:
# На самом первом шаге инерции нет, используем текущее значение
v_momentum = v
else:
# Совмещаем текущее значение с прошлым
v_momentum = self.alpha * v + (1 - self.alpha) * prev_V
# 3. Сохраняем новое состояние для следующего шага.
# .detach() используется, чтобы градиенты не текли через всю историю состояний,
# что превратило бы механизм в полноценный RNN и сильно усложнило бы обучение.
new_prev_V = v_momentum.detach()
# 4. Стандартный механизм self-attention
attn_scores = torch.matmul(q, k.transpose(-2, -1)) / (self.d_k ** 0.5)
attn_weights = F.softmax(attn_scores, dim=-1)
# Внимание применяется к инерционным значениям v_momentum
out = torch.matmul(attn_weights, v_momentum)
# 5. Собираем головы вместе и пропускаем через финальный линейный слой
out = out.transpose(1, 2).contiguous().view(B, T_q, D)
return self.W_o(out), new_prev_V
# Пример модели, которая использует MomentumAttention
class AutoregressiveModel(nn.Module):
def __init__(self, vocab_size, d_model, n_heads, alpha):
super().__init__()
self.embedding = nn.Embedding(vocab_size, d_model)
self.momentum_attn = MomentumAttention(d_model, n_heads, alpha)
self.layernorm = nn.LayerNorm(d_model)
self.ffn = nn.Sequential(
nn.Linear(d_model, 4 * d_model),
nn.ReLU(),
nn.Linear(4 * d_model, d_model)
)
self.out_proj = nn.Linear(d_model, vocab_size)
def forward(self, input_ids):
B, T = input_ids.shape
x = self.embedding(input_ids)
# Инициализируем состояние для всей последовательности
prev_V_state = None
all_step_outputs = []
# Цикл по каждому шагу (токену) в последовательности
for t in range(T):
# Берем срез данных для текущего шага
# В реальном декодере Q - это текущий токен, K и V - все предыдущие.
# Для простоты демонстрации механизма инерции, мы используем только текущий токен
# как Q, K, и V. Это показывает, как состояние `prev_V_state` передается.
current_x_step = x[:, t:t+1, :] # Shape: [B, 1, D]
# Вызываем слой внимания, передавая ему состояние с прошлого шага
attn_output, prev_V_state = self.momentum_attn(
Q=current_x_step,
K=current_x_step,
V=current_x_step,
prev_V=prev_V_state
)
# Стандартные блоки трансформера (residual connection, layernorm, FFN)
h = self.layernorm(current_x_step + attn_output)
step_output = self.ffn(h)
all_step_outputs.append(step_output)
# Собираем выходы со всех шагов в один тензор
full_output = torch.cat(all_step_outputs, dim=1) # Shape: [B, T, D]
# Финальная проекция в размер словаря
logits = self.out_proj(full_output)
return logits
# Параметры
batch_size = 4
seq_len = 10
vocab_size = 100
d_model = 64
n_heads = 8
alpha = 0.9
# Создаем модель
model = AutoregressiveModel(vocab_size, d_model, n_heads, alpha)
# Создаем случайные входные данные
input_ids = torch.randint(0, vocab_size, (batch_size, seq_len))
print(f"Входные данные (shape): {input_ids.shape}")
# Получаем выход модели
output_logits = model(input_ids)
print(f"Выходные логиты (shape): {output_logits.shape}")
# Проверка корректности размеров
assert output_logits.shape == (batch_size, seq_len, vocab_size)
print("nМодель успешно отработала")Что это даёт
-
Сглаживание представлений.
ВектораVне перескакивают резко между шагами прошлое состояние частично сохраняется, что снижает турбулентность активаций. -
Более стабильное распределение внимания.
Модель получает эффект инерции в значениях, и внимание не скачет при малых изменениях входа. Это особенно полезно в авторегрессионных моделях, где выходы сильно зависят от предыдущего шага. -
Облегчённое обучение.
Так какprev_Vпередаётся черезdetach(), градиенты не текут сквозь всю историю, что предотвращает взрыв или затухание градиентов в отличие от полного RNN-подхода. -
Простая интеграция.
Механизм не требует изменения архитектуры он полностью совместим с обычным MultiHeadAttention и может быть вставлен в любой трансформерный блок.
Возможные минусы
-
Накопление смещения (drift).
Еслиalphaслишком велико, старые состояния начинают тянуть новые векторные представления, и внимание может начать запоминать шум. -
Сложность выбора
alpha.
Значение 0.9 подходит не всегда при быстрых изменениях контекста модель может терять реактивность (поздно реагировать на новые токены). -
Невозможность параллелизации по времени.
Так как состояниеprev_Vпередаётся последовательно, обучение по всей последовательности становится менее параллельным (особенно при autoregressive setup). -
Потенциальная инерция ошибок.
Если модель делает ошибку на шаге t, она может частично переноситься дальше черезprev_V, особенно при большомalpha.
Заключение
Momentum Attention это шаг в сторону более живых архитектур.
Мы не просто учим модель смотреть на токены,
мы учим её чувствовать движение своего внимания как будто у неё появилась инерция восприятия.
Автор: YH7H22


