Reinforcement Learning: Model-free & Deep RL

Продолжаю погружаться в Reinforcement Learning. Здесь продолжение статьи Intro Reinforcement Learning.

Если предыдущая часть помогла вам понять, что такое среда, агент, награды и функции ценности, то здесь мы сделаем шаг дальше: мы переходим к model-free алгоритмам и Deep Reinforcement Learning, где агент учится оптимальной стратегии, не имея прямого доступа к модели среды.

Как и всегда, буду рада, если материал поможет кому-то в освоении RL.

Пользуясь случаем, оставляю тг-канал Not Magic Neural Networks.

Данный текст основан на курсах Practical_RL и MSU_AI 💜

1. Model-free RL

Рассуждения из Intro Reinforcement Learning были справедливы для относительно простых случаев, где нам была известна матрица переходов из одного состояния в другое. Однако, в реальных задачах это предположение часто не выполняется: среда может быть настолько сложной, что выразить вероятности переходов явно невозможно.

Пусть, например, мы хотим обучить агента парковать машину. Одно и то же действие (повернуть руль на 10° влево) может привести к разным результатам в зависимости от множества факторов: скорости автомобиля, сцепления с дорогой, погодных условий и поведения других машин. Поэтому невозможно явно задать вероятности переходов между состояниями для каждого действия.

Такие задачи, когда нам не известна модель среды, называют Model-free RL.

Самое очевидное что можно придумать – это попытаться выучить модель среды, просто насемплировав данных из взаимодействий агента со средой. Однако, на практике, выучить такое распределение оказывается сложнее, чем выучить оптимальную политику.

Возвращаясь к примеру с парковкой, люди как-то обучаются, не зная в точности как работает двигатель, тормозная система и взаимодействие всех датчиков (по-сути не зная модель среды). Становится понятно, что можно как-то обойтись без выучивания среды, а сразу получить алгоритм действия в этой среде.

Допустим, мы можем насемплировать различных MDP траекторий вида:

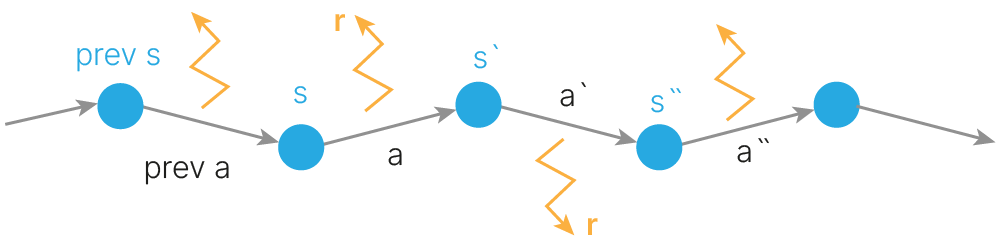
И, хотелось бы свести задачу к уже известным методам value iteration или policy iteration.

Поскольку по можно получить оптимальную политику (), то выгоднее учить ее. Для того чтобы получить оптимальную политику понеобходимо знать модель среды, однако сейчас речь про Model-free RL.

Можно посчитать среднюю дисконтированную награду по бесконечному количеству траекторий, которые проходят через состояние . То, каким образом при этом выбираются действия , будет описано ниже.

В этом заключается метод Монте-Карло.

1.1. Метод Монте-Карло:

1. Генерируем множество траекторий, содержащих конкретную пару

2. Оцениваем для всех траекторий.

3. Усредняем их для получения мат. ожидания

Довольно простой метод, однако, он требует слишком большого количества траекторий и их генерация может занять слишком много времени.

Например, для того чтобы обучить автомобиль парковаться, потребуются миллионы эпизодов, в ходе которых агент будет сталкиваться, застревать и совершать другие ошибки. Всё это необходимо лишь для того, чтобы постепенно выучить оптимальное поведение. Даже в симуляции такой процесс оказывается крайне трудоёмким: каждая траектория требует времени, вычислительных мощностей и хранения большого объёма данных.

Человек же может обучиться парковке ни разу не повредив свой автомобиль потому что умеет предсказывать последствия своих действий и оценивать будущее вознаграждение, не дожидаясь окончания всей траектории.

Эту идею можно перенести и в обучение с подкреплением. Вместо того чтобы ждать конца каждой траектории, мы можем оценивать ожидаемое будущее вознаграждение и обновлять его итеративно, используя математическое ожидание по будущим состояниям.

Такой подход называется Temporal Difference обучением (или TD-learning).

1.2. Temporal difference learning:

1. Инициализируем нулями.

2. Пока не сойдемся:

   1. Пересчитываем уравнение Беллмана:

      Только вместо математического ожидания честно разыгрываем траектории и усредняем:

   2. Обновляем с помощью скользящего среднего:

TD-learning (Temporal Difference learning) сочетает подходы методов Монте-Карло и динамического программирования. С точки зрения методов Монте-Карло, TD-обучение способно улучшать оценки прямо на основе опыта агента, без знания модели среды. С точки зрения динамического программирования, TD использует бутстрэппинг: обновляет оценки текущих состояний, опираясь на уже существующие оценки будущих состояний, не дожидаясь финального результата эпизода.

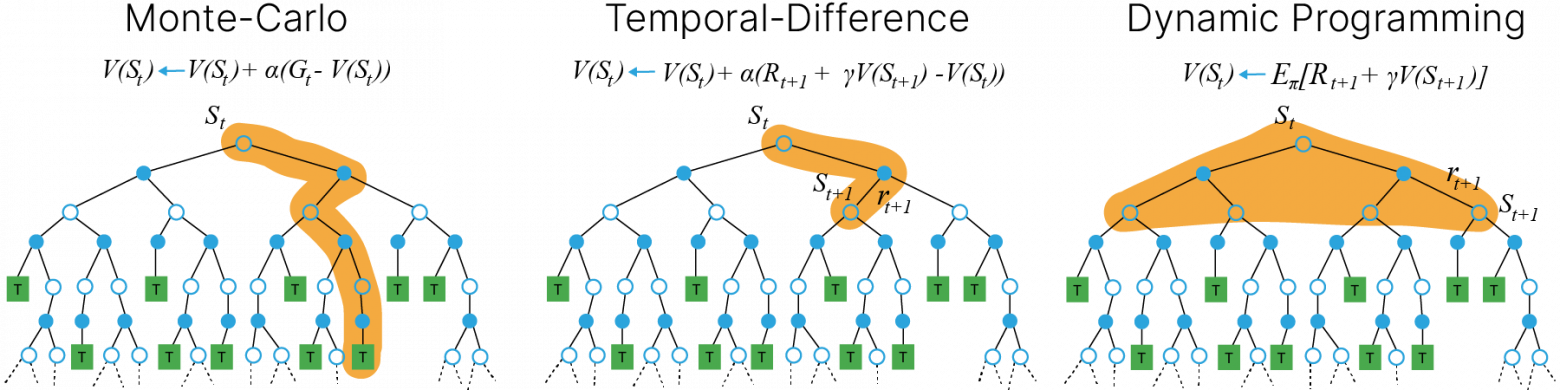
Частным случаем TD-обучения является Q-обучение.

1.3. Q-Learning

Рассмотрим кусочки траекторий вида: .

Посчитаем уравнение Беллмана только на таких траекториях:

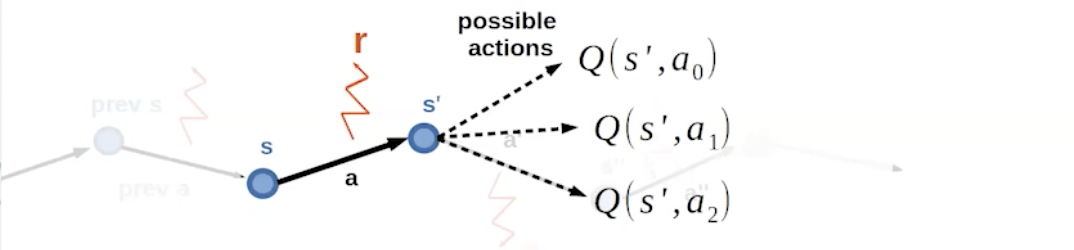
Аналогично, обновляем с помощью скользящего среднего:

Такой частный случай TD-learning называется Q-Learning:

1. Инициализируем нулями

2. Пока не сойдемся:

   1. Семплируем одну траекторию

   2. Считаем новое значение

   3. Обновляем

2. Как выбирать действие?

В алгоритмах выше не описано как именно выбирать действия для построения траекторий. С одной стороны, если выбирать действия случайным образом, мы обеспечиваем агенту исследование среды, но для сходимости алгоритма может потребоваться очень большое количество эпизодов. С другой стороны, если выбирать действия с максимальной ожидаемой наградой, то есть большой риск не оказаться в глобальном оптимуме (не выучить другие действия, которые агент еще не пробовал, но которые могут оказаться более оптимальными).

Эта дилемма известна как exploration-exploitation: exploration — стремление агента исследовать среду (выбирать случайные действия), exploitation — использование уже известных действий с наибольшей наградой.

2.1. – жадная стратегия

Простой способ сочетать исследование и использование знаний (exploration vs exploitation) – это выбирать с вероятностью случайное действие (exploration), а с вероятностью — действие с наибольшей ожидаемой наградой (exploitation).

В простейшей версии фиксировано, но на практике часто используют динамический . В начале обучения, когда мало данных и оценки неточные, делают большим и агент может больше исследовать. По мере обучения постепенно уменьшают и агент всё чаще использует жадный выбор, опираясь на накопленные знания.

Частный случай, когда стремится к нулю, называют предельно жадной стратегией.

2.2. Softmax стратегия

Можно выбирать действия пропорционально его ценности (Q-value):

где – параметр температуры, который контролирует баланс exploration/exploitation. Пристратегия становится жадной (только exploitation), при стратегия становится случайной (только exploration).

Таким образом, чем лучше действие (чем больше q-значение), тем выше вероятность, что его выберут, но даже плохие действия имеют небольшой шанс.

3. Off-policy & On-policy

Рассмотрим классическую задачу из обучения с подкреплением — Cliff World («Мир обрыва»). На изображении представлен grid-мир, где агент должен дойти от старта до цели. Нижний ряд клеток представляет собой обрыв (cliff): наступая на такие клетки, агент получает большое отрицательное вознаграждение (например, −10). Достижение цели, наоборот, приносит значительное положительное вознаграждение (+10).

Агент может пройти оптимальным, но рискованным маршрутом, проходящим вдоль обрыва, или выбрать более длинный, но безопасный путь.

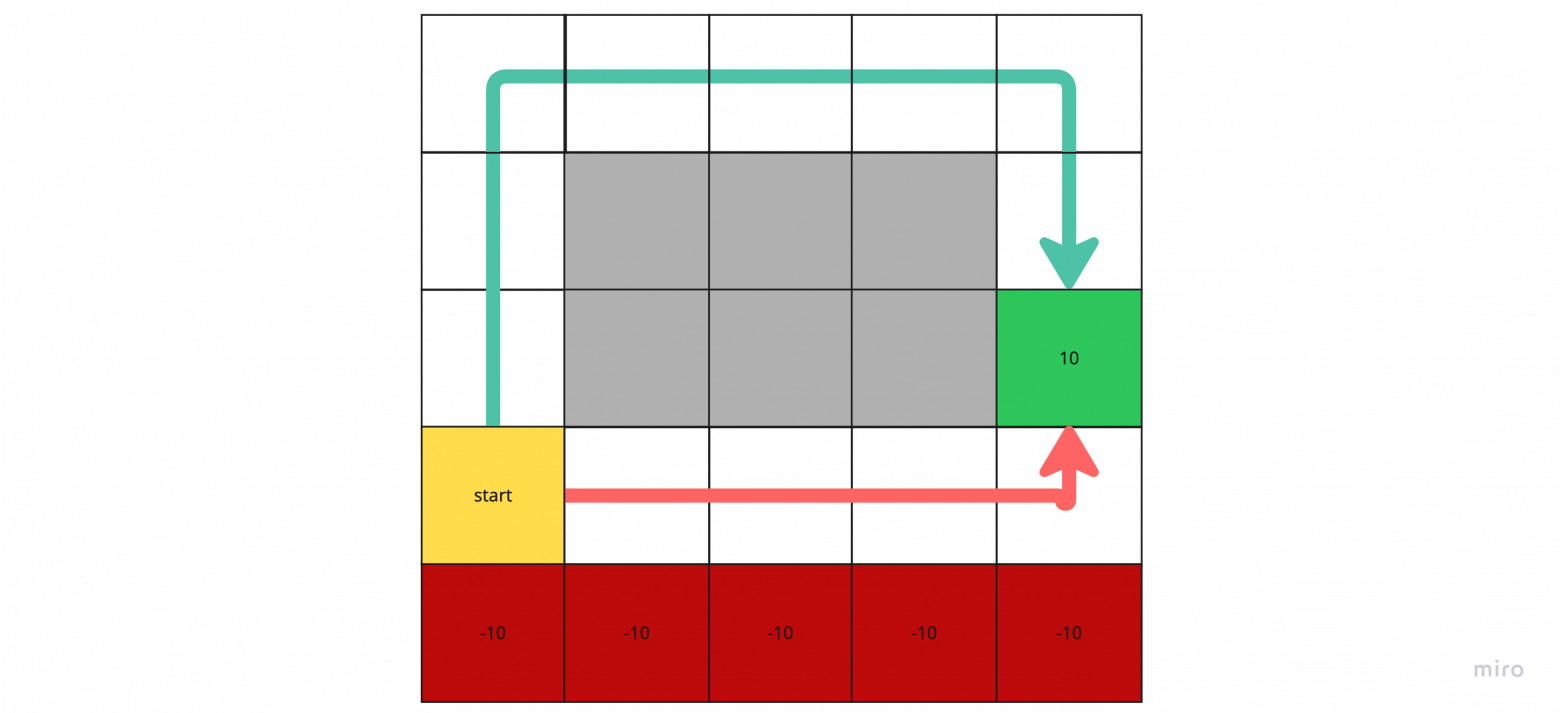
Если агент всегда выбирает действие с максимальным значением Q-функции, он будет следовать кратчайшему пути — то есть двигаться по краю обрыва, рискуя упасть и получить сильное наказание. Такой маршрут формально оптимален, но может оказаться нежелательным, если приоритетом является безопасность или стабильность поведения.

3.1. Off-policy

В Q-learning агент во время обучения выполняет действия ε-жадной стратегией, но обновляет ценности так, будто действует идеально жадно (target policy = greedy). Такие методы называются off-policy.

В Cliff World это приводит к рискованному, но оптимальному поведению — агент идёт по краю обрыва, стараясь быстрее достичь цели.

3.2. On-policy

В on-policy методах обучение и поведение агента происходят по одной и той же политике. То есть сам процесс исследования является неотъемлемой частью обучаемой политики.

Типичный пример — SARSA, где обновления Q-функции зависят от реально выбранных (возможно, не оптимальных) действий. Такой подход часто приводит к более безопасному поведению — агент избегает рискованных маршрутов, даже если они потенциально выгоднее.

В Cliff World агент, обучающийся по on-policy, выбирает более безопасный маршрут, избегая обрыва даже ценой увеличения длины пути.

3.3. SARSA (State-Action-Reward-State-Action)

В Q-learning мы обновляли политику скользящим средним , а новое q-значение вычисляли по формуле: .

Заменив максимум на математическое ожидание по текущей политике, мы получим on-policy алгоритм Expected SARSA:

Expected SARSA:

1. Инициализируем нулями.

2. Пока не сойдемся:

   1. Семплируем траекторию .

   2. Считаем новое значение на основе нашего выбранного действия в следующем состоянии , которое может быть не оптимально:
      

   3. Обновляем

Если в пункте 2.2. взять не математическое ожидание, а просто какое-то действие согласно политике, то алгоритм будет называться SARSA.

4. Deep Reinforcement Learning

Вернемся к уравнению обновляющее -функцию:

, где

Подставим в :

Раскроем скобку и вынесем :

Можно заметить, что такая запись чем-то похожа на шаг градиентного спуска, где – это learning rate, a – градиент.

Функция, у которой градиент является разницей – это :

,

По градиент брать не будем, его значение возьмем как константу (будем считать что это target) и обозначим его .

Видим, что формула и обновление совпадают с точностью до .
А -learning эквивалентен градиентному спуску со следующей функцией потерь:

Это наблюдение позволяет расширить представление о -значениях: вместо табличного хранения можно обучать параметрическую функцию — например, линейную регрессию или нейронную сеть.

Есть два основных подхода к проектированию нейронных сетей в RL:

1. Архитектура “Given s predict all q-values”:

   1. Сеть принимает на вход только “состояние” .

   2. На выходе сеть предсказывает все -значения для всех возможных действий одновременно.

   3. Такая архитектура более эффективна, так как за один проход по сети можно получить все значения и сразу выбрать действие с максимальным -значением. Это классическая архитектура для DQN (Deep Q-Network).

   4. Подходит только для дискретного пространства действий, так как размер выходного слоя фиксирован и равен числу возможных действий.

2. Архитектура “Given (s, a) predict Q(s,a)”:

   1. Сеть принимает на вход пару “состояние” и “действие”: .

   2. На выходе она предсказывает одно значение — -значение для этой конкретной пары.

   3. Подходит для случаев, когда пространство действий непрерывное или очень большое, так как сеть учится напрямую оценивать качество произвольного действия, без необходимости дискретизации.

   4. Чтобы выбрать оптимальное действие , приходится перебирать все возможные действия и вычислять для каждого. При большом или непрерывном пространстве действий это может быть вычислительно дорого.

Далее речь пойдет для первой архитектуры “Given s predict all q-values”, когда на вход принимается состояние s, а на выход q-значения для всех возможных действий в этом состоянии.

Данный подход может быть применен к алгоритму Q-learning, SARSА и Expected Value SARSA. Их отличие лишь в формуле обновления Q-values:

• Q-learning:

• SARSA:

• Expected Value SARSA:

Функция потерь для всех методов будет одинаковая:

Параметры нейросети будет обновлять обычным градиентным шагом, однако могут быть и более продвинутые методы, например, Adam.

5. Проблемы при обучении RL

Однако, вышеперечисленные методы будут плохо обучаться по следующим причинам:

1. Обучающие примеры в RL НЕ i.i.d. — они зависят из траектории агента.

   • i.i.d. – independent and identically distributed (независимые и одинаково распределённые)

   • Если агент, например, застрял в одной зоне среды, то он многократно видит почти одинаковые состояния и действия. Cеть переобучается на последние эпизоды и теряет обобщающую способность.

2. Модель может забыть части среды в которых давно не была.

   • Некоторые участки среды агент долго не посещает и эти состояния выпадают из тренировочного распределения. Это приводит к нестабильной политике (в одних частях среды агент ведёт себя оптимально, в других — случайно) и к “забыванию” как действовать в старых ситуациях.

5.1. Multi-agent reinforcement learning, MARL

Первый способ, доступный всегда, когда среда задана при помощи виртуального симулятора — запуск нескольких параллельных агентов. Разные агенты естественно исследуют разные части среды (разные эпизоды / состояния одновременно) — это повышает разнообразие данных и стабилизирует тренировки.

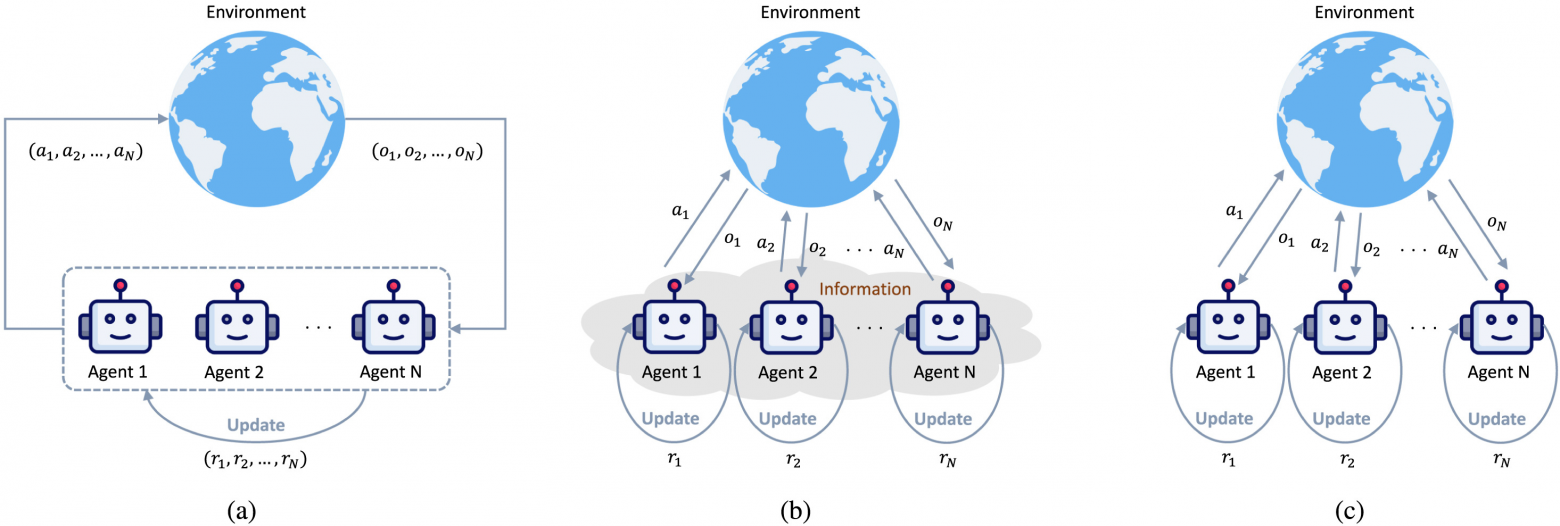
Существуют разные варианты MARL:

(a) Centralized Training and Centralized Execution, CTCE – когда у агентов единая политика.

(b) Centralized Training and Decentralized Execution, CTDE – когда у агентов единая политика при обучении, но при исполнении каждый агент действует независимо, используя только своё локальное наблюдение.

(c) Decentralized Training and Decentralized Execution, DTDE – когда агенты полностью обучаются и действуют самостоятельно, не имея доступа к информации других агентов.

5.2. Experience Replay Buffer

Вернемся к задаче “Cliff World”.

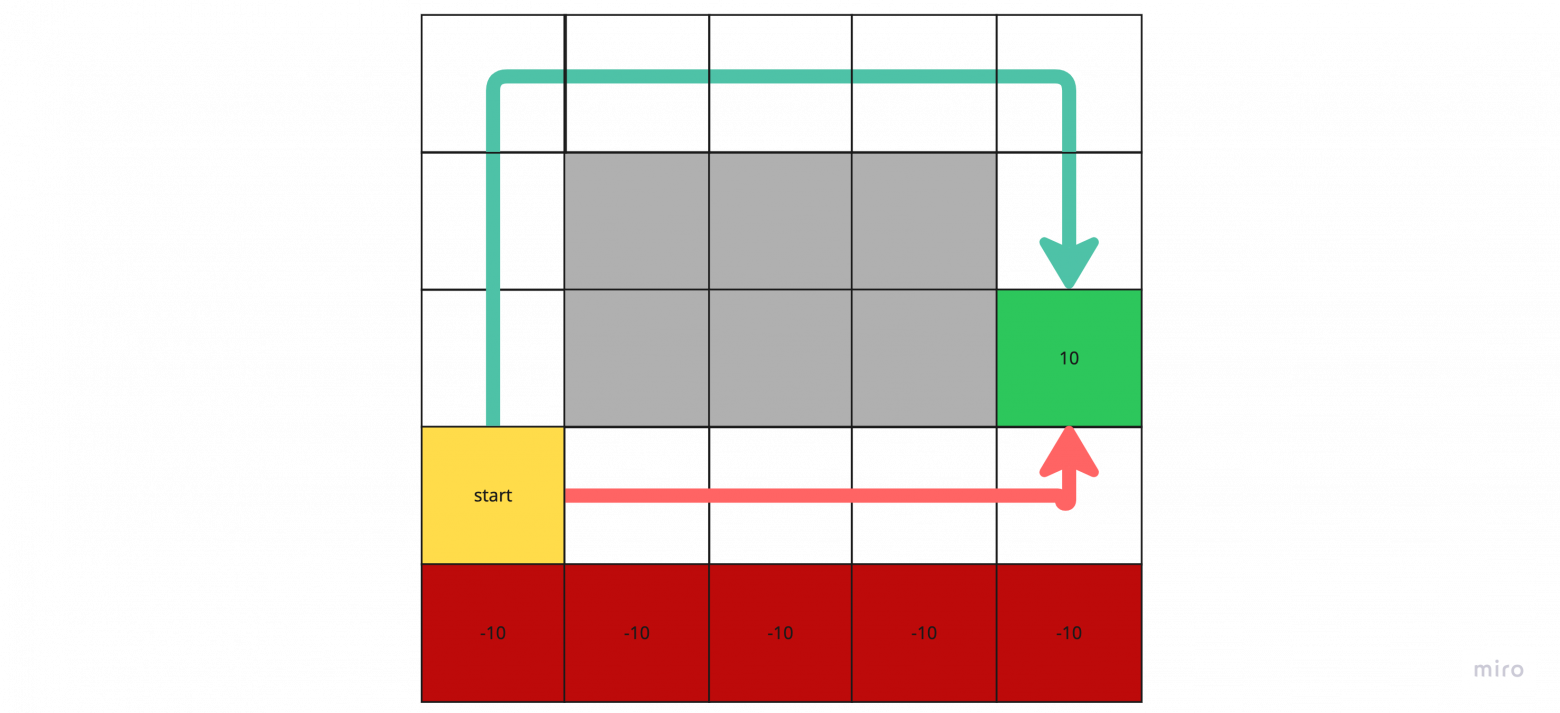
Агент делает действие, получает вознаграждение и сразу обновляет соответствующее значение. Однако, на картинке видно, что агент долгое время будет фактически обновлять нули, пока не дойдёт до награждающего состояния. Из-за этого обучение может быть неэффективным.

Однако, дойдя до конца эпизода, мы можем понять, какие действия вели к успеху, и скорректировать оценки состояний, которые этому предшествовали.

Так возникает идея хранить прошлый опыт и использовать его повторно.

Experience Replay Buffer — это специальный буфер (память), в котором хранятся прошлые взаимодействия агента со средой в виде переходов: .

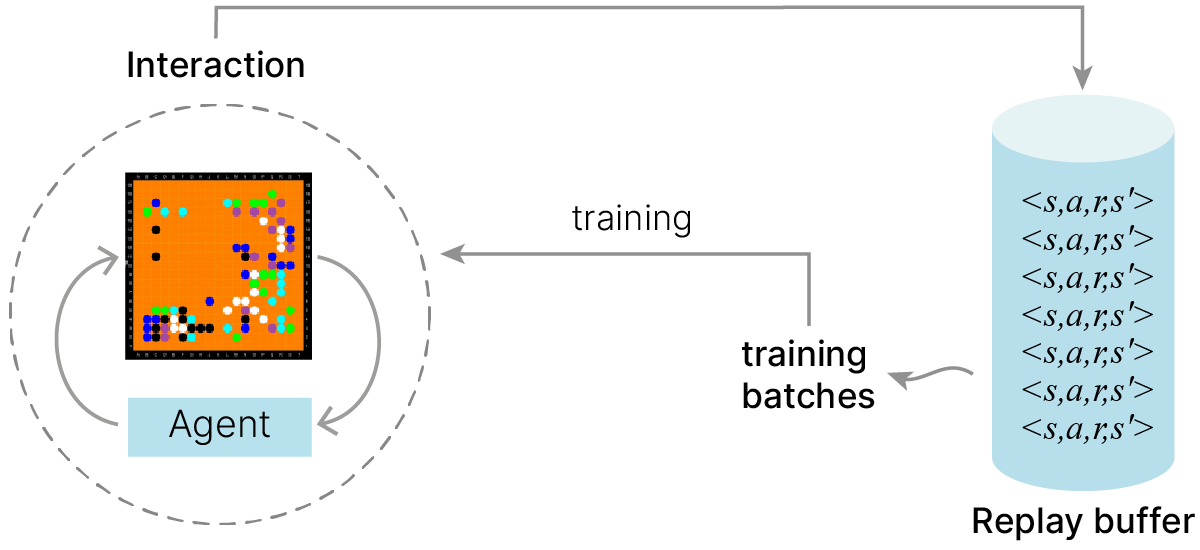
Вместо того чтобы обучаться только на последнем опыте, агент периодически выбирает случайный батч из буфера и обновляет параметры на его основе.

Однако Replay Buffer применим только к off-policy алгоритмам (Q-learning). Это связано с тем, что off-policy методы обновляют значения на основе целевой политики, отличной от политики, с которой собирались данные. Таким образом, даже плохие траектории не искажают обучение — они просто дают корректные оценки для состояний и действий, встречавшихся в прошлом.

В отличие от этого, on-policy алгоритмы (SARSA) оценивают ожидаемое вознаграждение именно под текущей политикой, поэтому использование старых, собранных под другими политиками переходов, может привести к смещению оценки.

Для DQN (Deep Q-Network) часто используют буфер размером 1 млн переходов.

5.3. N-gram trick

Во многих задачах RL предполагают обычную Марковскую цепь первого порядка — что будущее зависит только от текущего состояния .

Представим, что агент должен определять направление движения объекта, видя только его текущие координаты.

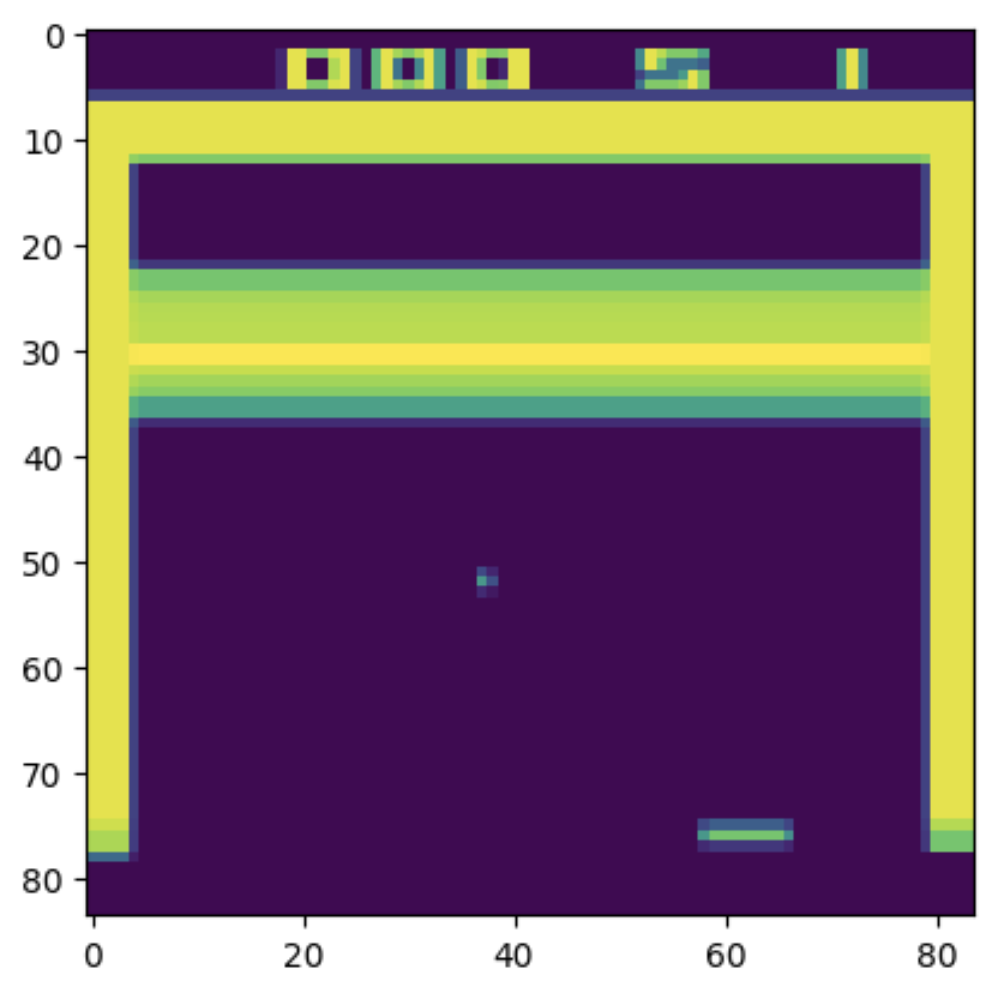
Если состояние — это просто позиция , то из одного кадра непонятно, движется ли объект вправо или влево / вверх или вниз. Но если агент видит два последних состояния , он может вычислить скорость и направление.

Можно использовать Nth-order Markov предположение – считать, что будущее состояние зависит от последних N состояний. То есть мы хотим предсказывать состояние или событие на основе прошлых N наблюдений.

То есть новое «расширенное состояние»будет достаточно для задачи выше.

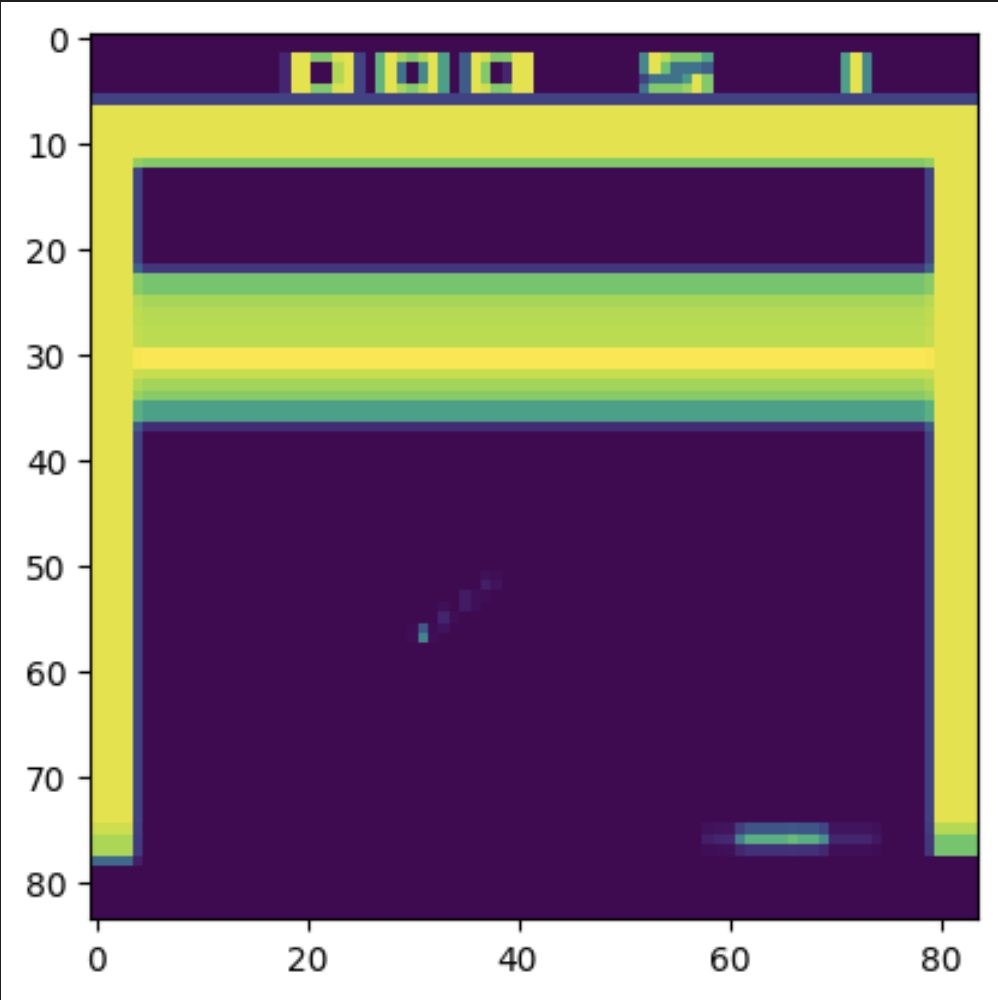
Данный трюк будет хорошо работать для сигналов с короткой памятью: скорость движения, таймеры.

Однако, при больших N он становится непрактичным.

5.4. Автокорреляция и Target network

Рассмотрим последовательность состояний, которые агент получает из среды.

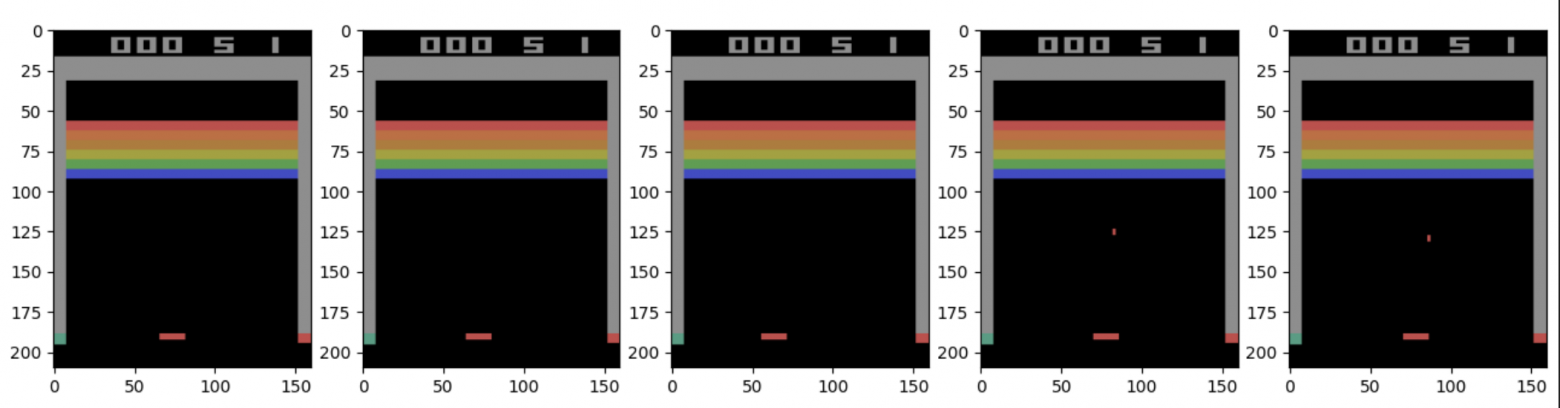
В большинстве задач соседние состояния очень похожи друг на друга: два соседних кадра в игре отличаются всего несколькими пикселями, а два соседних состояния в симуляции — минимальным изменением координат или скорости.

Так Q-сеть получает почти одинаковые входы подряд. Это означает, что и входы Q-сети сильно коррелированы. Когда мы обновляем параметры сети на одном состоянии, это обновление тут же влияет и на оценки для других, почти одинаковых состояний.

Проблема усиливается тем, что и текущая Q-сеть, и target из формулы используют одну и ту же функцию .

Из-за этого обновление становится самореференсным: сеть пытается приблизиться к target(у) → target в свою очередь тоже зависит от этой же сети → любое небольшое изменение параметров влияет и на предсказание, и на целевое значение.

Это может привести к ситуации, когда Q-сеть резко корректирует свои предсказания, что тут же меняет target. Возникает положительная обратная связь, в которой ошибка усиливает саму себя. В итоге градиенты могут начать “скакать”, веса — расходиться, а Q-значения — взрываться.

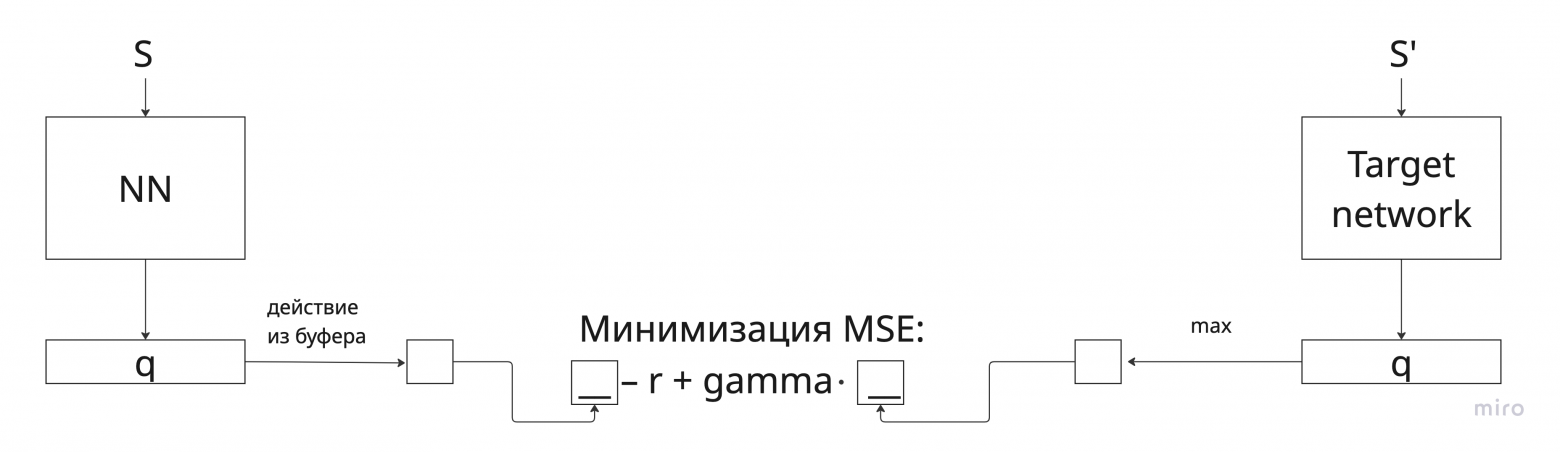
Проблему решают замораживанием функции которая оценивает качество следующего состояния.

где – основная сеть, — параметры (веса) основной Q-сети, – target сеть, – замороженные веса target сети.

Обучение будет выглядеть следующим образом:

Обновление весов можно делать разными способами:

• Hard target network делает обновление каждые шагов (~ 5000) путем копирования .

• Soft-target network обновляет на каждом шаге , где порядка 0.001.

Резюмируя

В model-free Reinforcement Learning агент учится исключительно на основе взаимодействия со средой, не имея доступа к её модели. Это приводит к необходимости оценивать будущее вознаграждение напрямую по траекториям, что реализуется через три ключевых класса методов:

1. Monte-Carlo (MC) — усреднение полной награды по эпизоду. Даёт несмещённые оценки, но требует большого числа полных траекторий и плохо масштабируется.

2. Temporal Difference (TD) — инкрементальное обучение, без ожидания конца эпизода.

3. Q-learning / SARSA / Expected SARSA — TD-обновления для функции действия-ценности. Различия между данными алгоритмами определяют поведение в задачах вроде Cliff World: off-policy методы изучают оптимальную (часто рискованную) политику, on-policy — более консервативную.

При выборе стратегии важно соблюдать баланс между exploration/exploitation.

Переход к нейросетям основан на том, что обновление Q-функции эквивалентно градиентному шагу по потере. Это позволяет вместо таблиц использовать параметрические функции​.

Однако, обучение будет разваливаться, если не костылить проблемы автокорреляции и “не i.i.d.” данных.

Practical_RL и MSU_AI 💜💜💜