Азбука тензорных сетей, часть 1: кружочки и палочки

Меня зовут Алексей Капранов, я архитектор-исследователь в команде квантовых вычислений в Cloud.ru. Сегодня я расскажу про подход, который позволяет не только моделировать большие квантово-механические системы, но и полезен для целого ряда задач, включая машинное обучение и нейронные сети.

И физики, и математики страдают от так называемого проклятия размерности, которое заключается в экспоненциальном росте сложности вычислений и необходимой памяти при увеличении числа параметров. Методы тензорных сетей позволяют существенно сократить этот скейлинг и в ряде случаев даже получить линейную сложность по количеству параметров и размерности задачи.

В этой части мы вспомним основы тензорной алгебры и на простых примерах узнаем, что же такое тензорная сеть и как представлять операции с тензорами в виде комбинации палочек и кружочков.  

Дисклеймер и о чем будут эти статьи

Как уже понятно из названия, цель данных статей познакомить читателя с замечательным миром тензорных сетей. Этот рассказ нацелен на достаточно широкую аудиторию, знакомую с линейной алгеброй, и я старался изложить материал максимально просто и доступно. Несмотря на то что данные методы пришли из квантовой физики, в основе лежит все та же математика, которая является универсальной. Такой подход часто называют квантово-вдохновленным (quantum-inspired), но это тема для отдельной дискуссии. Не пугайтесь, для понимания знания физики совершенно не нужны.

Этот обзор разделен на две части, в которых я расскажу про то, что такое тензорные сети и мы «от печки» получим самое простое и наиболее изученное тензорное разложение, которое может «исцелить» от «проклятия размерности».

В первой части будет дана основная мотивация, а также напоминание, что такое тензоры и почему с ними удобно работать именно в графическом представлении. Фактически, здесь будет рассказан теоретический минимум, чтобы читатель мог дальше понимать «птичий язык» данной области.

Вторая же часть будет посвящена уже более прикладным идеям. А именно сингулярному разложению и самому простому и наиболее изученному тензорному разложению — Tensor Train (TT) decomposition, оно же тензорный поезд. Не переключайтесь, впереди много интересного.

Введение в введение в тензорные сети

Самый резонный вопрос читателя, открывшего эту статью и дочитавшего до этого момента: «А зачем мне все это надо? Зачем столько слов и оговорок? Нельзя ли сразу дать мне фреймворк с инструкцией и не душнить?». Мой ответ достаточно простой: «Нет, нельзя». Во-первых, без этих знаний не будет понятно как и почему это работает, что (по крайней мере, мне) доставляет огромную головную боль. Во-вторых, чтобы не объяснять по нескольку раз одно и то же, и не отвечать на одни и те же вопросы, я решил, что лучше написать статью на Хабр, где будет некий необходимый минимум по этому вопросу и основные ответы.

Любое введение содержит в себе ссылки на предыдущие работы, и особенно приятно, что тензорные сети вышли за пределы квантовой физики благодаря работе нашего соотечественника и директора AIRI Ивана Валерьевича Оселедца. Практически весь русскоязычный материал про тензорные сети и представление тензорного поезда написан им и его учениками: докторская диссертация Оселедца, публичные выступления, кандидатские диссертации учеников, публичные выступления и статья на Хабре, где можно найти ссылки на основные результаты их группы, библиотека для работы с TT.

В публичном же поле для массового пользователя рассказано очень мало, что является большим упущением. Объясняется это достаточно просто: исследователи нечасто пишут популярные статьи. Про это мне сразу вспоминается очень точная мысль, которую редактор сказал Стивену Хокингу: «Каждая формула, включенная в книгу, вдвое сокращает число читателей», но надеюсь, если формулы простые, то удастся победить такое проклятие размерности.

Цель этих двух статей как раз в том, чтобы максимально закрыть этот пробел, учитывая, что тензорные представления постепенно «вылезают» из области фундаментальных исследований в более прикладное направление. Насколько хорошо у меня получилось, покажет лишь время и ваша оценка, но все равно кто-то должен был это сделать. Ну ладно, хватит лирики, давайте уже перейдем к делу.

Что такое тензоры?

Вы можете открыть Википедию и умереть от формулировки, но не переживайте, это нормально. А теперь закройте Википедию. Сейчас мы попробуем подумать про это на достаточно простом языке (продвинутым читателям, которые хотят освежить/углубить знания в тензорной алгебре, советую замечательный цикл из 18 статей про тензорную алгебру на Хабре).

В физике и математике тензоры появились естественным путем для формулировки законов природы на языке, который не будет зависеть от смены системы координат. Появление такого обобщения кажется вполне естественным, поскольку в физике мы часто сталкиваемся с описанием трехмерного и четырехмерных пространств (координаты плюс время). Этот язык плюс-минус сформировался в 1900—1920-е года (Ричи, Леви-Чивита, Энштейн и др.).

Если говорить более формально, то тензор — это обобщение векторов и матриц (объектов с одним и двумя индексами), которые преобразуются определенным образом при смене координат (перестановке индексов). Сразу отмечу, что количество индексов ассоциируется с размерностью, то есть их число равно размерности. В контексте же тензоров размерность принято называть рангом (не путать с другим рангом в линейной алгебре, который есть количество линейно-независимых строк/столбцов), мы вернемся к этому чуточку позднее.

Мы будем рассматривать более простую картину, как это обычно принято в компьютерных науках. А именно будем считать тензор просто многомерным массивом, то есть объектом с несколькими индексами. Нам все равно на геометрию и физику, мы пытаемся научиться говорить на новом диалекте, сейчас это просто обобщение векторов и матриц на большую размерность.

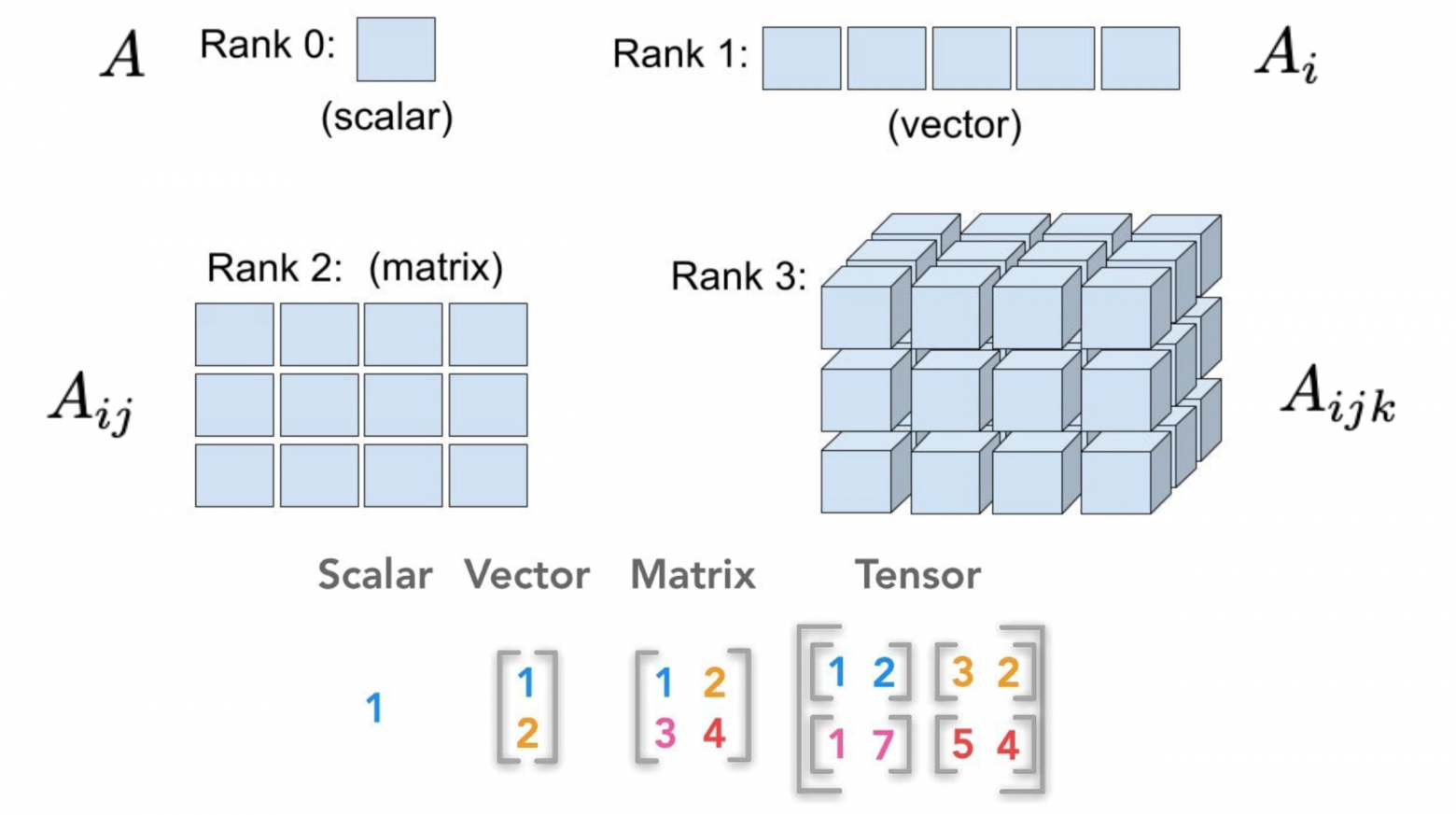
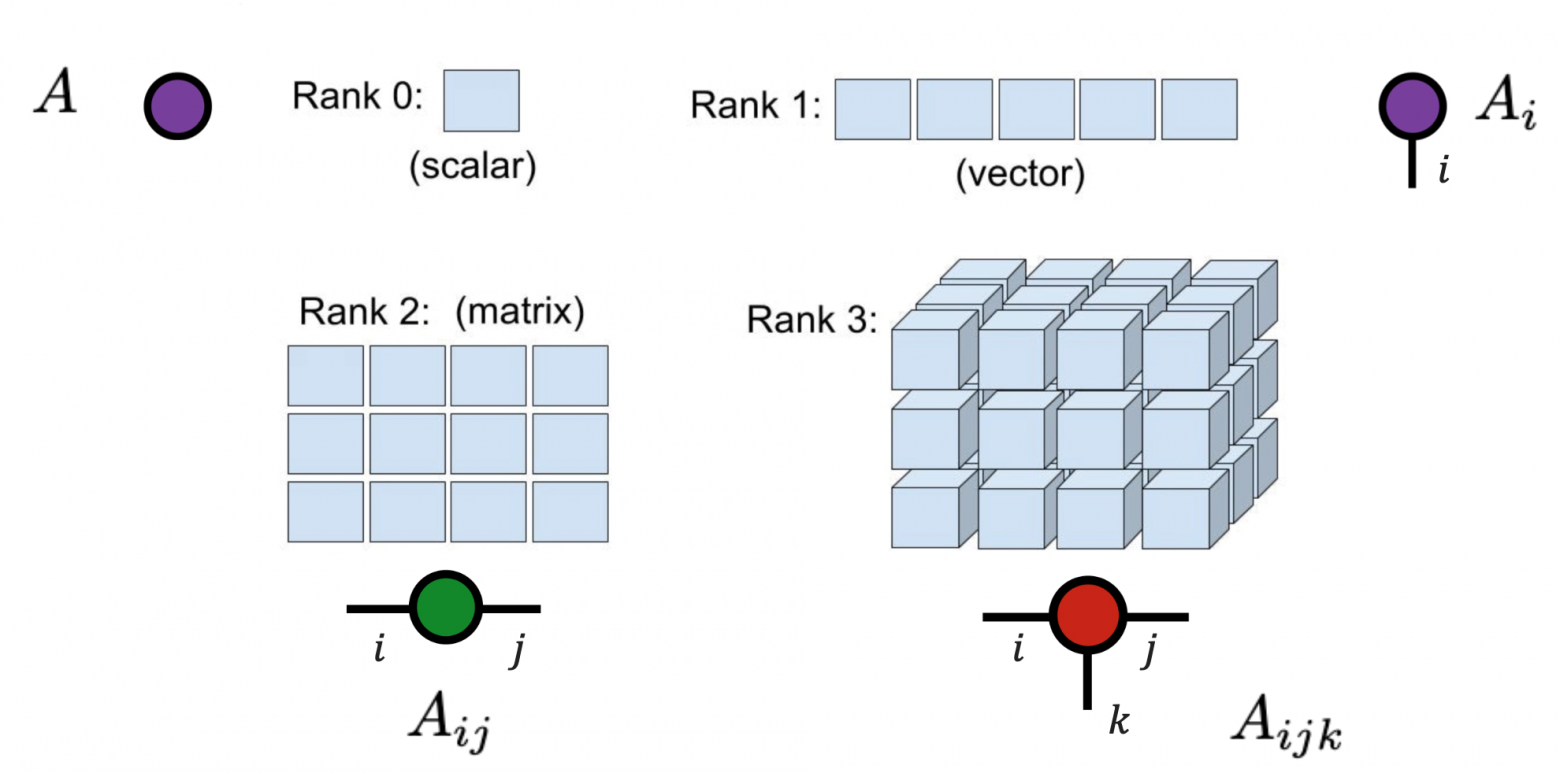
Как я уже упомянул выше, в контексте тензорных представлений принято использовать индексы, чтобы лучше это прочувствовать, разберем следующий пример, изображенный выше.

Пойдем по порядку:

• Левый верхний угол: если у нас всего один элемент, то у него нулевая размерность или же нулевой ранг. То есть это просто скаляр, у которого нет размерности. Соответственно, у скаляра нет индекса (нет адреса в массиве, по которому он «прописан»). Таким образом, скаляр обозначается просто как

  

• Правый верхний угол: теперь мы записали скаляры в определенном порядке и получили массив, у которого «адрес» каждого элемента однозначно определяется одним числом. В таком случае мы имеем один индекс, то есть размерность/ранг равную единице. Это называется тензором первого ранга или вектором и обозначается как

• Левый нижний угол: увеличим размерность массива еще на единицу и получаем матрицу, то есть массив из массивов. Тогда любой элемент матрицы можно получить, задав два числа. Таким образом, это тензор второго ранга и обозначается как

• Правый нижний угол: пойдем дальше и сделаем массив из массивов, которые содержат массивы. Браво, мы получили объект с тремя индексами, то есть каждый элемент теперь задается тремя числами. Это тензор третьего ранга, который обозначается как

Также стоит отметить, что обычно тензоры с рангом меньшим тройки не принято называть тензорами, а для простоты их называют скалярами, векторами и матрицами. Вы и так это знаете, краткость — сестра таланта (краткости у меня нет). Сразу оговорюсь, что в данном изложении я пишу индексы у тензоров снизу, но без потери общности я могу писать их только сверху, это вопрос определения. Более сложные случаи, когда появляется разница между написанием индексов сверху и снизу, я не рассматриваю (если хотите узнать подробнее про это, то опять же, смотрите замечательный цикл статей про тензорную алгебру, на который я ссылался выше).

Зачем это нужно: проклятие размерности и суть спасения

Человечество научилось прекрасно приближать матрицы различными способами. Потом мы поговорим про методы сингулярного и QR разложений, которые практически всегда оказываются несправедливо забыты в университетских курсах линейной алгебры. Основная идея всех этих методов заключается в том, что мы можем представить (факторизовать) матрицу как произведение двух и более матриц с более низким рангом (здесь уже ранг в контексте линейной независимости строк/столбцов). Это называется низкоранговой аппроксимацией, и с ее помощью, мы можем хранить значительно меньше элементов нежели в изначальной матрице, что серьезно облегчает вычисления.

В качестве иллюстрации этой идеи на рисунке ниже приводится частный случай такого разложения, где мы представили матрицу с 16 значениями в виде произведения двух векторов, содержащими по 4 элемента каждый, которые мы просто угадали. Таким образом, каждый элемент матрицы представляется в виде произведения значений из каждого вектора.

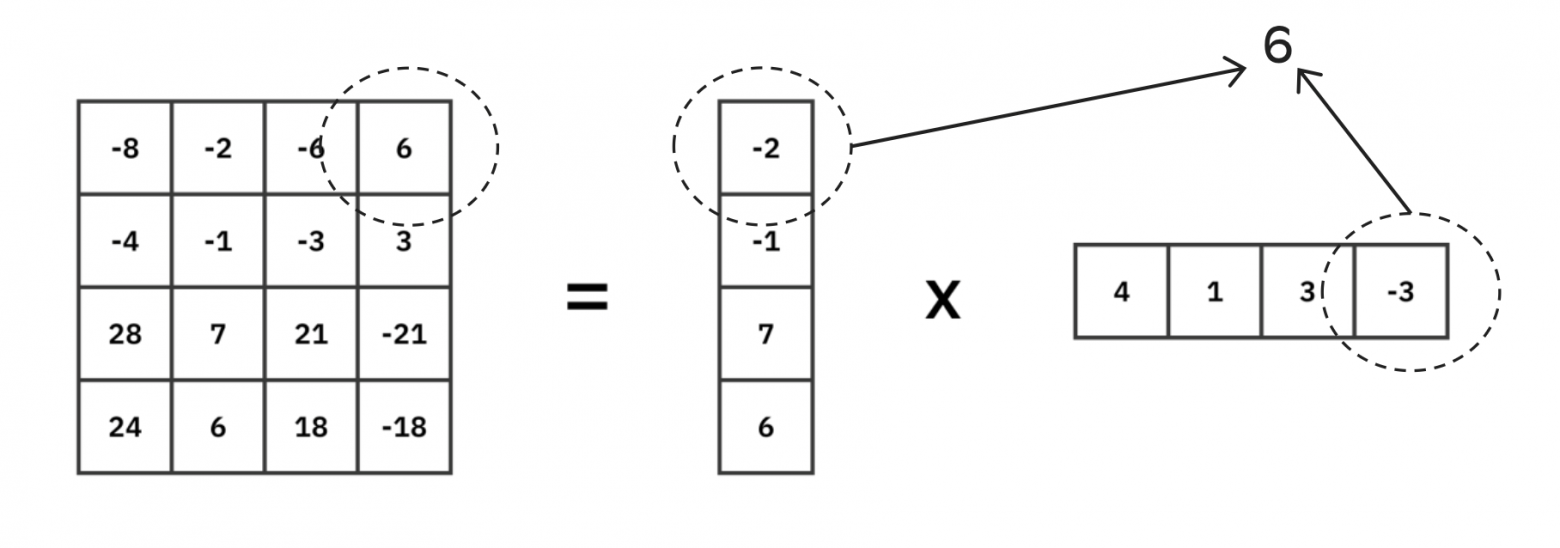
Отлично, получается, мы умеем работать с матрицами, но тогда зачем нам вообще потребовались тензоры? Почему мы не можем просто дальше использовать матрицы, для которых мы можем построить низкоранговое представление? Ответом на этот вопрос служит так называемое проклятие размерности (англ. curse of dimensionality).

Впервые это понятие ввел математик Ричард Беллман. Он использовал этот термин применительно к общей задаче динамического программирования для описания экспоненциального роста сложности задачи по мере увеличения пространства признаков. Отмечу, что физики обычно цитируют не оригинальную работу Беллмана, а нобелевскую лекцию Уолтера Кона, который ее получил за развитие методов функционала плотности в квантово-механических системах. Кон в своей лекции рассматривал проблемы, связанные с размерностью и сложностью в таких системах, но на Беллмана не ссылался и напрямую не называл это «проклятием размерности».

Современная формулировка «проклятия размерности» звучит так: при увеличении размера пространства параметров возникает экспоненциальный рост сложности задачи

где d — это количество параметров, а N — это размерность пространства. Очевидно, что это очень неприятная асимптотика и с ней надо как-то бороться. Именно здесь и появляется идея использовать тензорные разложения.

Самым простым и наиболее изученным на текущий момент является так называемое представление тензорного поезда (англ. Tensor Train (TT)), в физике же оно известно как Matrix Product State (MPS). Оно позволяет существенно снизить алгоритмическую сложность до линейной по количеству параметров и размерности задачи. То есть асимптотика будет

где r — это максимальный ранг разложения.

Надеюсь, что мы поняли, за что мы сражаемся и основательно замотивировались. В следующей части мы детально разберем, как получить TT представление тензора и что такое максимальный ранг разложения, а пока нам предстоит понять «азбуку» тензорных сетей.

Язык кружочков и палочек: как визуализировать сложное

Для более удобной работы с тензорами придумали специальную технику, в которой все операции представляются графически, и значительная часть головной боли (и ужаса) при взгляде на формулу пропадает. Этот язык обладает универсальностью и простой, а также является общепризнанным в современных работах по тензорным сетям. Поэтому я собираюсь не просто вас «накормить рыбой», но и «дать удочку», чтобы вы могли потом самостоятельно разобраться. 

Вы и так знаете, что графические представления всегда лучше, ведь нам проще воспринимать картинки. Важно лишь то, чтобы эти картинки можно было понять.

Свертка тензоров

Сейчас я напомню в очередной раз про очевидные для многих вещи, но именно на них мы и потренируемся в графическом представлении. Из линейной алгебры мы знаем, что вектора и матрицы определенных размеров можно перемножать. Существует обобщение на случай большей размерности, и оно называется свертка. Для нас это оказывается очень важным, так как по аналогии с матричными разложениями, где матрица представляется в виде произведения нескольких матриц меньшего ранга, мы хотим получить разложение для тензора. Логично предположить, что такое представление будет некой сверткой тензоров меньшей размерности.

Итак, пойдем от простого к сложному и вспомним, как работает произведение векторов.

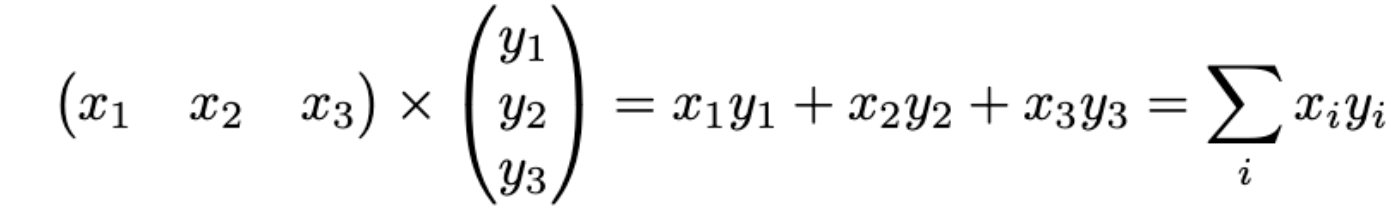
Рассмотрим пример произведения векторов, также известный как скалярное произведение, которое является частным случаем свертки. Мы здесь суммируем произведения по индексу i или же сворачиваемся по этому индексу.

Аналогичную кухню мы имеем при произведении матриц.

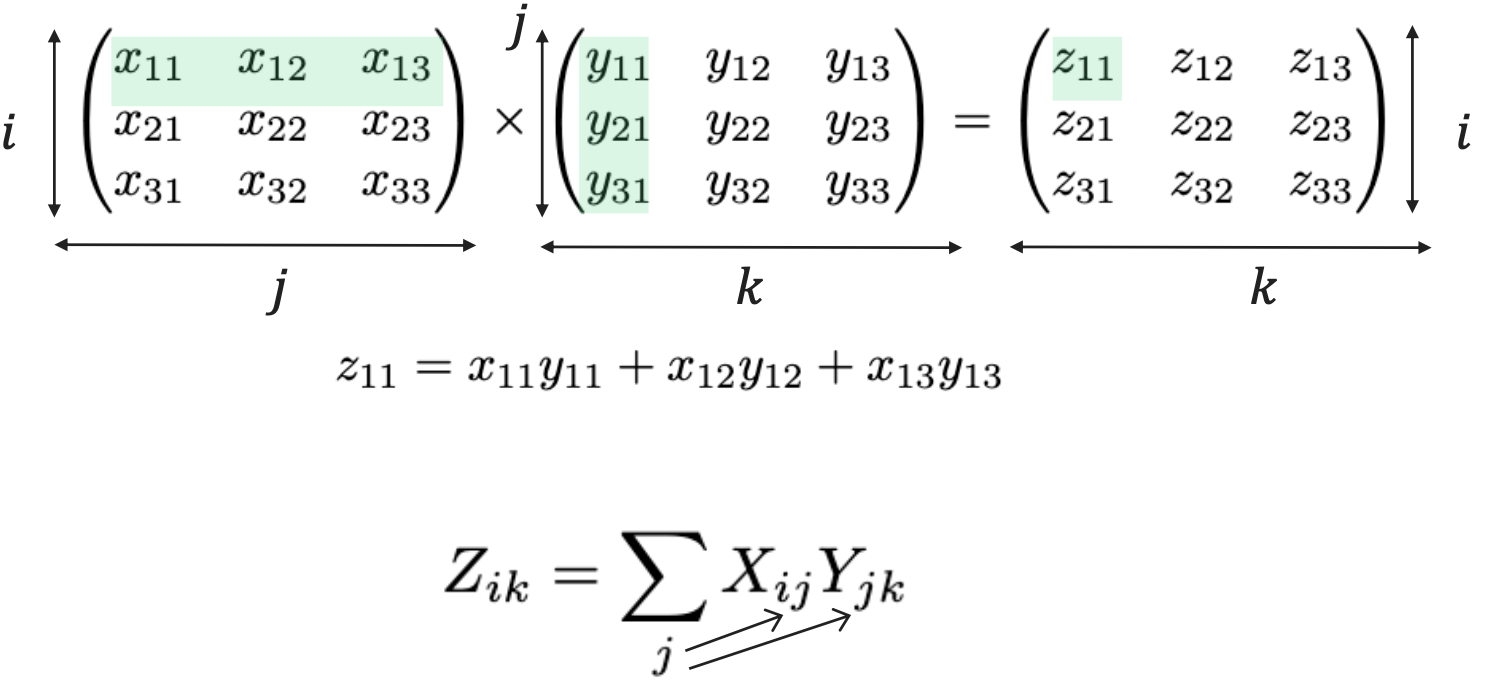
При произведении двух матриц мы проводим ту же свертку по одному индексу. То есть мы перемножаем элементы и складываем по этому индексу, как это изображено в примере на рисунке выше.

Абсолютно аналогично это работает для тензоров, где мы сворачиваемся по одному или нескольким индексам. Ниже приводится пример такой свертки по двум индексам.

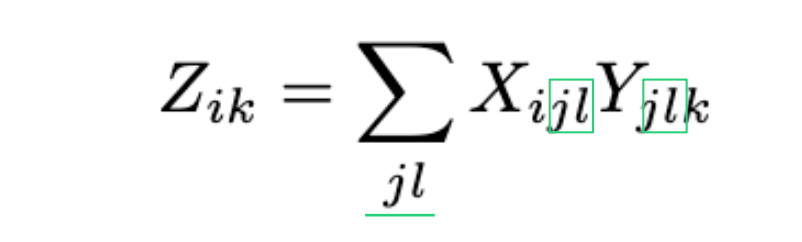
Таким образом, свертку можно сравнить с многомерным скалярным произведением. Мы, по сути, берем два и более тензора, выбираем совпадающие индексы, перемножаем элементы и складываем по этим индексам. Ниже мы разберем эти же примеры, но на языке тензорных сетей.

Также стоит отметить, что достаточно часто в свертках игнорируют знак суммы, считая, что она происходит по повторяющимся индексам (их еще называют немые). Это называется правило суммирования Энштейна. Я не буду здесь его использовать и буду везде оставлять знак суммы, но имейте в виду, что такое правило есть, и нередко бывает, что авторы забывают сказать, что они его используют, чем вводят читателя в замешательство.

Про графическое представление

На этих простых примерах не очень понятно, а зачем же нужно это графическое представление. Сейчас мне придется причинить читателю чуть больше боли и привести пример огромной свертки.

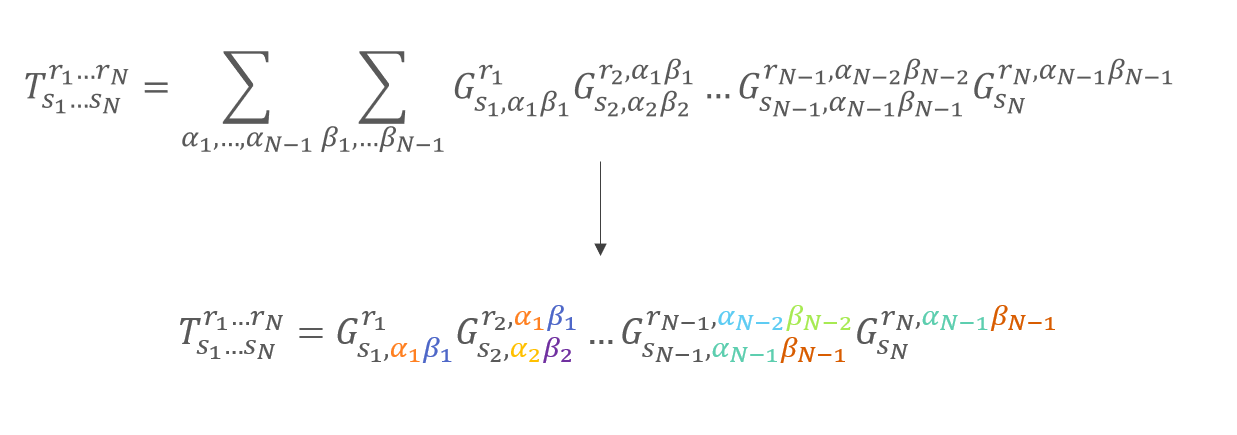
Как я говорил выше, тензоры могут иметь еще и индексы сверху, но нам не обязательно сейчас понимать, зачем это надо, а цель данной картинки лишь устрашение. Согласитесь, чтобы понять эту формулу надо потратить несколько минут (или часов/дней), а к тому же пройти все 5 стадий принятия. Для более интуитивной работы с такими конструкциями, которые нередко встречаются в теоретической физике, Роджер Пенроуз в 1971 году предложил представлять свертки в виде картинок.

Чтобы понять, как нам это сделать, начнем опять с простых примеров и посмотрим еще раз на самый первый пример, но теперь однозначно сопоставим массивам графическое представление.

На уже знакомой нам картинке мы видим, что появились какие-то кружочки с палочками. Что это такое? Каждому объекту ставится в соответствии кружочек, а количество палочек (часто называют эти палочки ногами) это количество индексов или же ранг данного тензора. Таким образом, мы получаем следующее:

• Тензор нулевого ранга (скаляр) — кружочек без палочек.

• Тензор первого ранга (вектор) — кружочек с одной палочкой, то есть одним индексом.

• Тензор второго ранга (матрица) — кружочек с двумя палочками, то есть объект с двумя индексами.

• Тензор третьего ранга — кружочек с тремя палочками или же объект с тремя индексами.

Вроде бы все просто, но зачем нам выдумывать такие обозначения? Это надо для того, чтобы более наглядно представлять, по каким индексам идет свертка и тогда существенно проще понять структуру свертки и результирующего тензора.

Теперь мы можем переписать операции свертки, которые мы рассматривали ранее, в графическом представлении. Все, что нам надо это соединять кружочки по нужным индексам.

Начнем разбираться с простого произведения векторов. В таком случае мы имеем два кружка с одной ножкой, и мы соединяем эти ножки (см. рисунок 8). Когда мы провели свертку по какому-то индексу, то этот индекс/палочка исчезает. То есть на выходе мы должны получить про кружок без палочек, то есть скаляр.

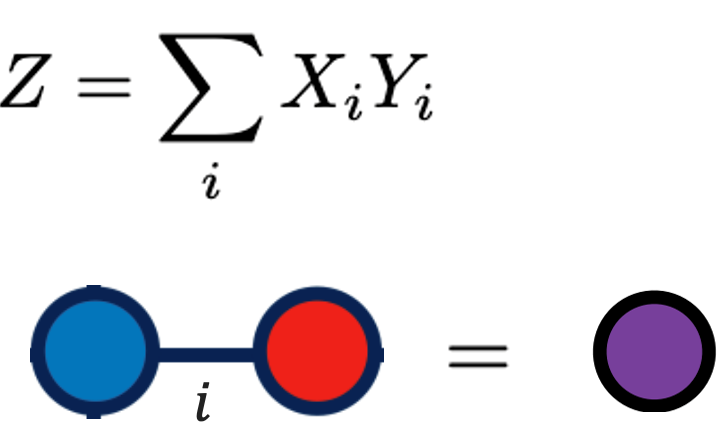
Вроде бы общий принцип понятен, продолжим расширять наше понимание и рассмотрим произведение матриц. Это свертка двух объектов с двумя индексами по одной из палочек. То есть, мы получаем, что одна ножка остается на месте, а другая участвует в свертке. Следовательно, общая ножка исчезает, так как по ней идет свертка, и в результате мы получаем кружок с двумя ножками, то есть матрицу, как мы и ожидали.

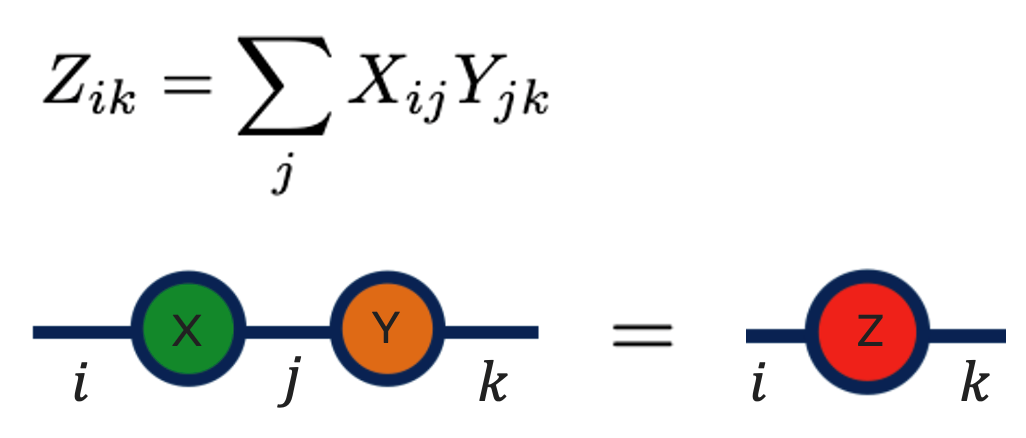
Теперь еще раз посмотрим свертку двух тензоров сразу по двум индексам. Что мы имеем? У нас есть два кружка, каждый из которых имеет три палочки. Мы сворачиваемся по двум индексам, то есть у каждого тензора в операции участвует по две палочки. То есть две палочки у каждого исчезают из-за свертки и по одной остается. Соответственно, в результате мы получаем кружок с двумя палочками, то есть с двумя индексами как на формуле.

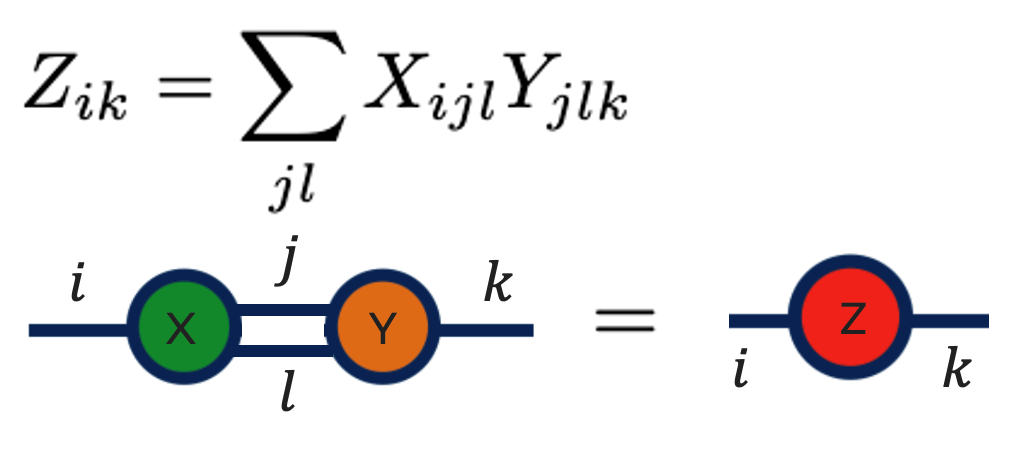
Таким образом, мы увидели на примерах, как используется графическое представление для тензоров. Теперь мы можем абсолютно естественно сказать, что же такое тензорная сеть.

Представление тензора в виде тензорной сети означает, что оно может быть определено с помощью других тензоров (кружочков), которые соединены между собой общими индексами (палочками). Для того чтобы получить тензор, необходимо провести свертку по этим индексам (соединить нужные палочки).

Reshape

Казалось бы, мы уже знаем графическое представление, разве этого недостаточно для успешного тензорного разложения? Нет, мы прошли лишь часть пути. Чтобы действительно эффективно работать с тензорами, мы должны знать еще несколько вещей.

Нам важно понимать, что мы практически свободны в выборе ранга тензора, но с единственным ограничением — количество элементов должно сохраняться. Это абсолютно логичное требование.

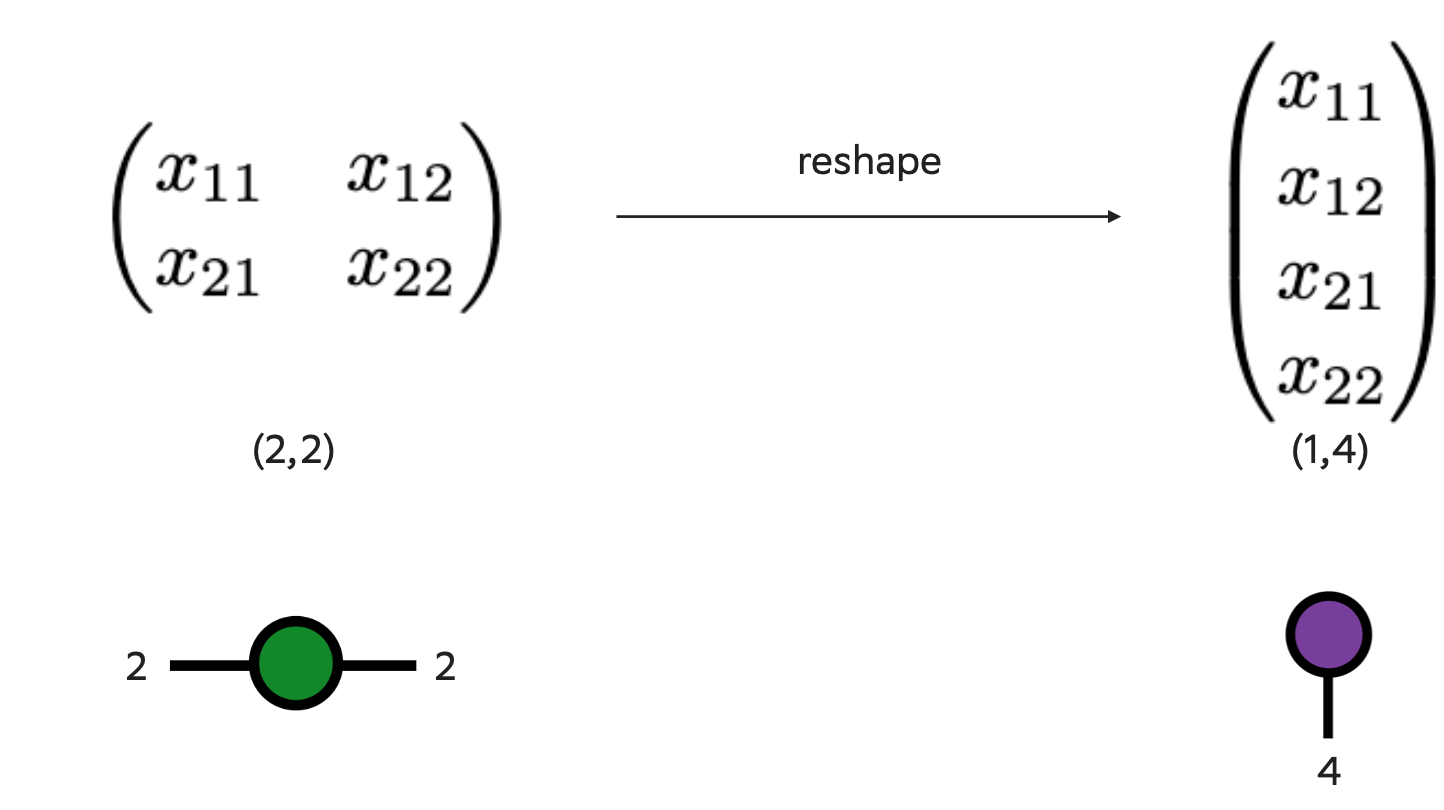
Например, я могу переписать матрицу 2х2 как вектор из четырех элементов. Если бы я попытался записать эту матрицу как вектор пяти элементов, то я бы не смог. Также я могу переписать эту матрицу как тензор 4 ранга с размерами (1,1,1,1).

Сразу отмечу, что именно таким образом, я могу уйти от матричного представления в сторону тензорного, которое и позволит нам бороться с «проклятием размерности».

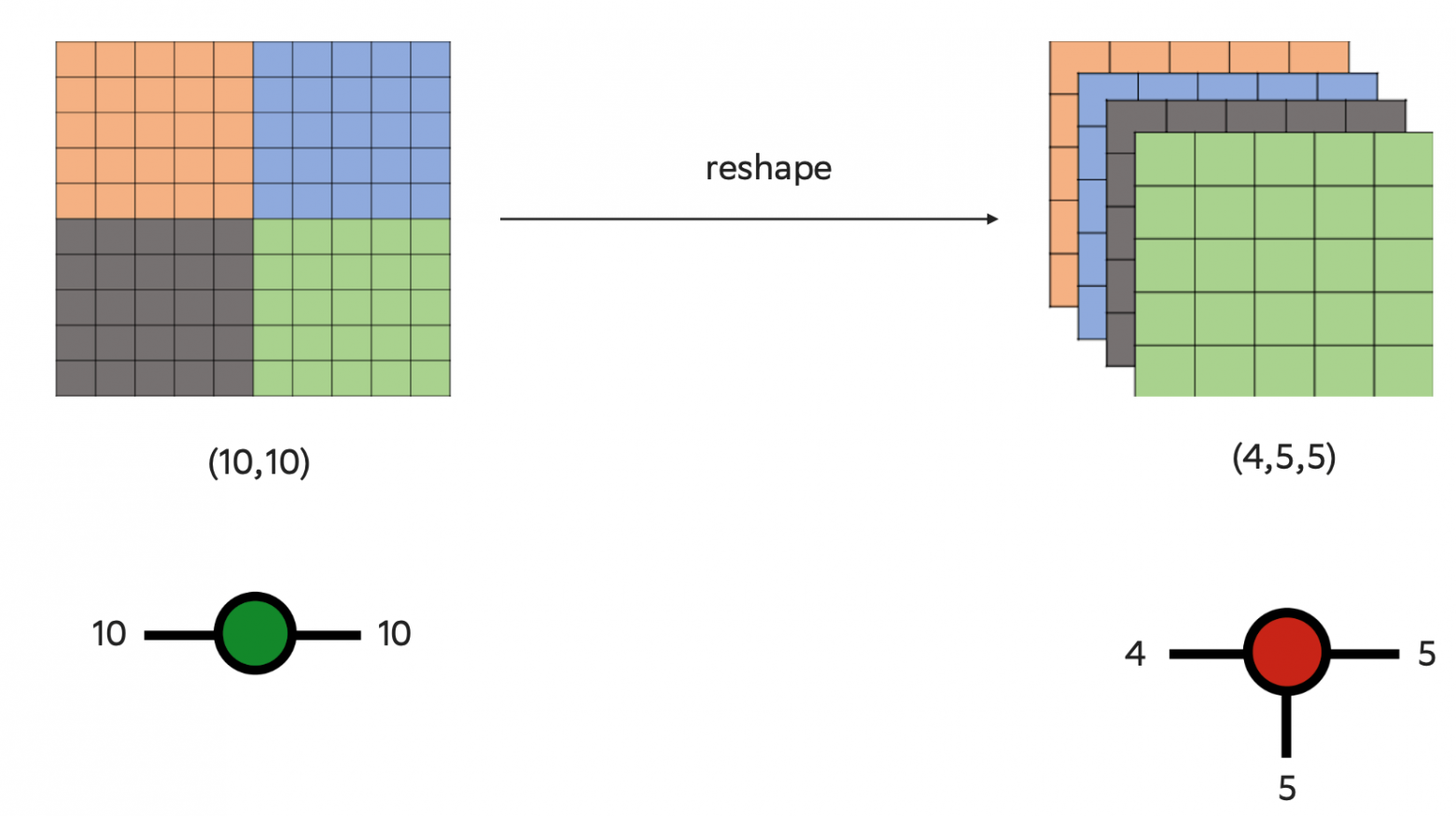
Рассмотрим еще один пример: мы можем переписать матрицу размерами 10х10 (всего 100 элементов) как тензор третьего ранга. То есть мы записываем вектор, который состоит из четырех матриц 5х5, то есть у нас все те же 100 элементов.

Вычислительная сложность

Когда мы имеем более сложные структуры свертки (то есть из более чем двух объектов), то возникает неоднозначность в порядке свертки, что может приводить к ненужной вычислительной сложности. Посмотрим, что же это такое на примерах.

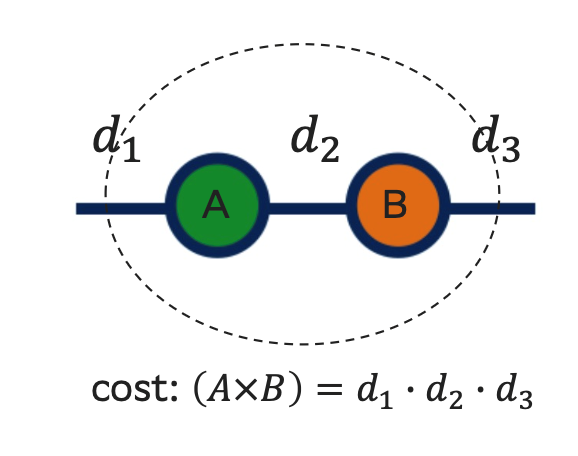
Вычислительная сложность свертки определяется количеством палочек, которое принимает участие в операции, то есть, грубо говоря, сколько нам элементов надо перемножить и сложить друг с другом. На рисунке выше изображен пример определения вычислительной сложности произведения двух матриц. В операции принимают участие два кружочка и три палочки (по одной свертка, а две другие свободны). Таким образом, сложность будет произведением размерности ножек, то есть

В примере выше у нас не было выбора в каком порядке сворачивать индексы, так как способ всего один. Но если в свертке участвует уже более двух тензоров, то мы вольны в выборе порядка свертки. Это приводит к разной вычислительной сложности в зависимости от порядка операций.

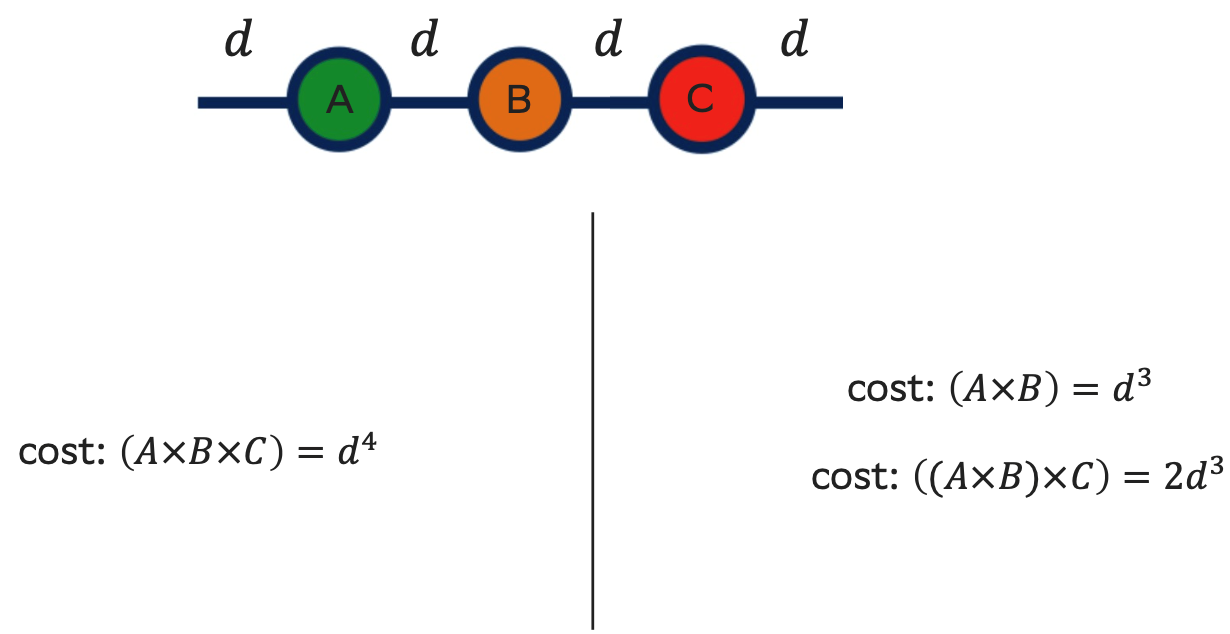
Рассмотрим более сложный пример, изображенный ниже, где мы выполняем свертку трех матриц. У нас есть два способа получить ответ: (1) посчитать все «в лоб», (2) свернуть сначала два тензора (A и B или B и C) и затем свернуть с оставшимся (C или A). Будем для простоты считать, что размерность всех индексов одинаковая и равна d. Тогда в первом случае в операции участвуют все ножки, и, следовательно, получаем общую сложность O(d⁴). Во втором случае мы сначала сворачиваем, например, A и B (прямо как в прошлом примере) за O(d³). Свернув A и B, мы получаем матрицу и сворачиваем с C (то есть опять ситуация, как в примере выше). Эта операция аналогично выполняется за O(d³). Таким образом, общая двух операций сложность

что лучше, чем вычисления «в лоб» с O(d⁴).

import numpy as np
# пусть все размерности совпадают и равны 5
d = 5
# инициализируем матрицы со случайными значениями
A = np.random.rand(d,d) 
B = np.random.rand(d,d)
C = np.random.rand(d,d)
# способ 1: считаем "в лоб"
# то есть
# A * B * C -> ABC
ABC1 = np.zeros((d,d))
for i in range(d):
    for j in range(d):
        for k in range(d):
            for l in range(d):
                ABC1[i,l] += A[i,j]*B[j,k]*C[k,l]
            
# способ 2: считаем поочередно
# то есть
# A * B -> AB
# AB * C -> ABC
ABC2 = np.zeros((d,d))
AB = np.zeros((d,d))
# получаем вместо одно наивного цикла
# с вложенностью 4 два цикла 
# с вложенностью 3
for i in range(d):
    for j in range(d):
        for k in range(d):
            AB[i,k] += A[i,j]*B[j,k]

for i in range(d):
    for k in range(d):
        for l in range(d):
            ABC2[i,l] += AB[i,k]*C[k,l]

Выводы первой части

Сегодня вы узнали (и, надеюсь, даже поняли), что такое тензорные сети и зачем они нужны. На простых примерах мы познакомились с графическим представлением, элементарными операциями и определением алгоритмической сложности.

Если кому-то эти примеры и рассуждения показались слишком простыми, то я этому очень рад, так как в этом и заключается цель этой (и следующей статьи) — дать теоретический минимум про тензорные сети максимально простым языком с самых основ.   

В следующей части мы обсудим сингулярное разложение и получим простейшее низкоранговое тензорное разложение — тензорный поезд.

Встретимся здесь же на Хабре, жду вас тут, никуда не уходите!