Глубокое обучение: Слой линейного преобразования и полносвязная нейросеть. Теория и реализация на самодельном autograd

Всем привет. В этой статье я расскажу про слой линейного преобразования. Идею для реализации я взял из книги «Грокаем глубокое обучение». Здесь рассмотрим как использовать самодельный алгоритм автоматического дифференцирования при создании и обучении нейросети, про который я сделал разбор ранее.

Меня зовут Алмаз Хуснутдинов. Я занимаюсь проектом “Теория цифрового интеллекта” – бесплатный и открытый проект, направленный на развитие мышления в направлении создания программы, обладающей интеллектом.

Если вам не нужно разбираться в том, как работает нейросеть на низком уровне, то просто прочитайте ту часть статьи, где рассказывается про использование слоев и реализацию нейросети.

Содержание: идея слоя прямого распространения, новые операции: операция умножения и деления матрицы на число, линейный слой и дополнительный функционал, задача «логическое или», как происходит обучение линейного слоя и набор данных digits.

Ведение

В глубоком обучении слой линейного преобразования, также известный как полносвязный слой (fully connected layer, dense layer, linear layer), является фундаментальным компонентом многих типов нейронных сетей, включая полносвязные нейронные сети, рекуррентные или сверточные.

В полносвязном слое каждый нейрон текущего слоя связан со всеми нейронами предыдущего слоя. Это означает, что каждый нейрон в полносвязном слое получает входные сигналы от всех нейронов предыдущего слоя, и каждая такая связь имеет свой весовой коэффициент.

Но под слоем прямого распространения я имею в виду не только линейное преобразование. Такие слои как: функция ошибки, функция активации, свертка, пулинг, сглаживание (flatten), нормализация, обратная свертка (экспанирование, expand, развертывание) и вообще любой другой слой, который принимает на вход один вектор признаков (или один тензор признаков) и возвращает тоже один вектор признаков (one to one).

Основная идея слоя линейного преобразования

Принцип работы полносвязного слоя заключается в прямом распространении сигнала через себя и его линейном преобразовании. Сначала входные данные или данные с предыдущего слоя передаются на вход. Затем каждый нейрон в полносвязном слое вычисляет линейную комбинацию входных данных, используя веса и смещения. Результат линейной комбинации пропускается через функцию активации, например, relu, sigmoid, tanh, которая добавляет нелинейность в модель.

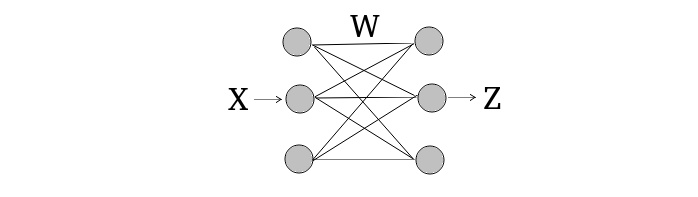
Серым цветом на рисунке обозначен входной вектор X и выходной вектор Z. Линейное преобразование вектора X осуществляется его произведением на матрицу весов, в результате получается новый вектор Z, причем векторы X и Z не обязательно одинакового размера. Также прибавляется вектор смещения, то есть к каждому элементу вектора Z прибавляется какое-то свое число, которое также как и веса изменяется в процессе обучения.

Процесс прямого распространения сигнала через полносвязный слой:

z – выходное значение слоя (линейная комбинация весов и входного значения и сложение с вектором смещений), размерность вектора z равна числу нейронов на выходе линейного слоя, х — входной вектор, размерность равна числу нейронов на входе в линейный слой, W – матрица весов, в которой каждая i-я строка содержит веса для соответствующего i-го нейрона на выходе слоя, b — вектор смещений, каждый элемент этого вектора суммируется с соответствующим элементом полученного вектора Wx.

Далее полученное значение z передается в функцию активации:

f – функция активации (relu, sigmoid, tanh и другие). По факту функция активации это не слой, а просто применение какого-то преобразования над элементами вектора, просто оно производится сразу над всеми числами в массиве (происходит распараллеливание вычислений на низком уровне, если используются специальные библиотеки, такие как та, на основе которой работает модуль numpy в python).

Для обучения полносвязной нейронной сети используется метод обратного распространения ошибки. Этот метод позволяет вычислить градиенты ошибки относительно весов и смещений, что необходимо для обновления параметров сети во время обучения (на основе градиентного спуска). Процесс включает в себя вычисление ошибки на выходном слое, а затем распространение этой ошибки назад через сеть, обновляя веса и смещения на каждом слое.

Новые операции для самодельной системы autograd

В другой статье я сделал разбор алгоритма autograd, а в этой — я покажу как его использовать в глубоком обучении. Добавим в систему пару новых операций: умножение на число и деление (на число). У операции умножения на число производная вычисляется просто умножением на число, а для деления немного сложнее:

Не забываем, что в числителе нужно умножить на значение производной с предыдущего шага.

Нужно изменить операцию умножения:

def __mul__(self, other, data=None):  # умножение на тензор или число с правой стороны
    if isinstance(other, float) or isinstance(other, int):
        data = num_mul_matrix(other, self.data)

    elif isinstance(other, Tensor):
        data = mul_matrixes(self.data, other.data)

    return Tensor(
        data=data,
        creators=[self, other],
        operation_name="__mul__"
    )

def __rmul__(self, other):  # умножение на число с левой стороны
    return self.__mul__(other)

Добавляем дополнительные условия для того, чтобы отдельно умножать матрицу на матрицу или матрицу на число. rmul – это операция умножения на число с левой стороны от тензора, просто используем ту же логику умножения mul.

Обратное распространение для умножения на число нужно немного изменить:

if self.operation_name == "__mul__":
    self_grad = grad * self.creators[1]  # new Tensor
    self.creators[0].backward(self_grad)

    if isinstance(self.creators[1], Tensor):
        other_grad = grad * self.creators[0]  # new Tensor
        self.creators[1].backward(other_grad)

Здесь нужно проверить, что второй операнд является тензором, а не числом, так как нам не нужно вычислять производную для числа и у него нету метода backward.

Теперь операция деления матрицы на число или числа на матрицу:

def __truediv__(self, other, data=None):  # разделить на число или на тензор
    if isinstance(other, int) or isinstance(other, float):
        data = matrix_div_num(self.data, other)

    elif isinstance(other, Tensor):
        data = matrix_div_matrix(self.data, other.data)

    return Tensor(
        data=data,
        creators=[self, other],
        operation_name="__truediv__"
    )

def __rtruediv__(self, other):  # разделить число на тензор
    return Tensor(
        data=num_div_matrix(other, self.data),
        creators=[other, self],
        operation_name="__rtruediv__"
    )

Тут нужно реализовывать отдельно, так как производная для операции деления вычисляется по-разному для каждого операнда. Для деления матрицы на число или на матрицу делаем отдельные условия в методе truediv. А для деления числа на матрицу делаем отдельный метод rtruediv.

Обратное распространение для операции деления. Для этих двух методов нужно реализовать похожую логику:

elif self.operation_name == "__truediv__":
    self_grad = grad / self.creators[1]
    self.creators[0].backward(self_grad)

    if isinstance(self.creators[1], Tensor):
        other_grad = (-self * grad) / (self.creators[1] * self.creators[1])
        self.creators[1].backward(other_grad)

elif self.operation_name == "__rtruediv__":
    other_grad = (-self * grad) / (self.creators[1] * self.creators[1])
    self.creators[1].backward(other_grad)

Вычисляем для операндов-создателей производную по правилу дифференцирования для операции деления. Делаем условие, если делитель является тензором, то вычисляем для него производную, если это число, то не вычисляем. А для деления числа на матрицу просто вычисляем производную для матрицы.

Простая реализация

Рассмотрим обычные матрицы чисел и преобразования над ними.

from tensor import *

inputs = [[2, 1], [1, 3]]  # in_features = 2
weights = [[0.1, 0.2], [0.3, 0.4]]  # out_featurea = 2
bias = [[0.1, 0.1]]

z = matrix_by_matrix(inputs, weights)  # out_featurea = 2
print(z)

expanded_bias = expand_item(item=bias[0], dim=0, copies_num=2)
print(expanded_bias)

z = add_matrixes(z, expanded_bias)
print(z)

h = sigmoid(z)
print(h)

output:
[[0.5, 0.8], [0.9999999999999999, 1.4000000000000001]]
[[0.1, 0.1], [0.1, 0.1]]
[[0.6, 0.9], [1.0999999999999999, 1.5000000000000002]]
[[0.6456563062257954, 0.7109495026250039], [0.7502601055951177, 0.8175744761936437]]

Создаем матрицу весов, у которой каждый столбец является весами, которые относятся к каждому соответствующему выходному нейрону для линейного слоя. Входных признаков 2 и выходных 2. В матрице входных значений каждый вектор признаков представлен в виде строки, каждая строка матрично умножается на матрицу весов, в итоге получается матрица векторов выходных значений. Потом к каждому получившемуся выходному значению прибавляем значение смещения, для этого нужно его скопировать 2 раза, так как на вход передается 2 примера — копируем вектор смещения для каждого входного примера. Затем применяем функцию активации сигмоиду.

Все вспомогательные функции реализованы на чистом python в другом файле.

Слой линейного преобразования

Сначала создадим общий класс, который будет интерфейсом (понятие из ООП) для различных типов слоев, в этом классе будут определены общие для всех слоев поля и методы.

class Layer:
    def __init__(self):
        self.parameters = []

    def get_parameters(self):
        return self.parameters

Каждый слой должен содержать список своих параметров, которые нужно обучать, метод для обработки входных данных (это метод forward, который в этом примере куда-то пропал) и метод для получения параметров слоя.

Теперь создадим класс для линейного преобразования.

class Linear(Layer):
    def __init__(self, in_features, out_features):
        Layer.__init__(self)

        self.weights = Tensor(rand((in_features, out_features)))
        self.bias = Tensor(rand((1, out_features)))
        self.parameters.append(self.weights)
        self.parameters.append(self.bias)

Наследуем его от общего класса. Создаем поля для весов и смещений, инициализируем и добавляем в список параметров слоя тензоры весов и смещений.

def forward(self, inp):
    out = inp.dot(self.weights)
    out += self.bias.expand(0, inp.shape()[0])

    return out

В методе forward матрично умножаем матрицу признаков на матрицу весов. Копируем смещения столько раз, сколько на входе векторов признаков и прибавляем. Все как в простой реализации.

Теперь сделаем слой, который будет обрабатывать несколько линейных слоев, он называется последовательным. Этой слой можно использовать для работы с нейросетью прямого распространения — то есть такой, в которую на вход подается пример в виде одного элемента (вектор, матрица, тензор), а на выходе получается тоже один вектор, а внутри нейросети не происходит каких-то других преобразований кроме как прямого распространения сигнала.

class Sequential(Layer):
    def __init__(self, layers: list):
        Layer.__init__(self)
        self.layers = layers

    def add(self, layer):
        self.layers.append(layer)


    def forward(self, inp):
        for layer in self.layers:
            inp = layer.forward(inp)

        return inp


    def get_parameters(self):
        parameters = []

        for layer in self.layers:
            parameters += layer.get_parameters()

        return parameters

Наследуем его от общего класса. На вход ему передаем список из различных слоев прямого распространения, он работает только со слоями, у которых преобразование типа «один вход и одни выход» (one to one). Добавляем метод add для добавления в него новых слоев. В методе forward последовательно будут обрабатываться входные данные с каждого предыдущего слоя. В методе get_parameters соединяем все параметры всех слоев в один список параметров и передаем его.

Оптимизация и функция ошибки

Для того, чтобы изменять параметры слоев, можно создать специальные объекты, которые будут оптимизировать модель на основе различных методов градиентной оптимизации. Создадим класс для обычного градиентного спуска.

class GradientDescent:
    def __init__(self, parameters, lr=0.1):
        self.parameters = parameters
        self.lr = lr

    def zero(self):  # занулить градиент
        for param in self.parameters:
            param.grad.data = zeros(shape=param.grad.shape())

    def step(self, zero=True):
        for param in self.parameters:
            param.data = sub_matrixes(param.data, num_mul_matrix(self.lr, param.grad.data))

        if zero:
            self.zero()

Эта структура принимает на вход параметры слоев и значение скорости обучения. В методе zero происходит обнуление градиентов всех слоев, чтобы они не накапливались с предыдущих итераций обучения. В методе step происходит шаг градиентного спуска и обнуление градиента.

Для функции ошибки можно создать отдельный слой. Этот слой не будет содержать параметров, он лишь выполняет преобразование функции ошибки.

class MSELoss(Layer):
    def __init__(self):
        Layer.__init__(self)

    def forward(self, output, target):
        samples_num = output.shape()[0] * output.shape()[1]
        return ((output - target) * (output - target)).sum(dim=0).sum(dim=1) / samples_num

В метод forward передаем выход модели и целевое значение. Вычисляем общее число признаков по всем примерам (так как мы оптимизируем функцию сразу по всем выходным признакам) и делим на него квадрат суммы разницы выходов и целевых значений, возвращаем значение функции MSE — это будет двумерный список с одним единственным числом — значением функции MSE.

Задача «логическое или»

Рассмотрим крошечную нейросеть для решения задачи «логическое или». Эта задача состоит в том, чтобы нейросеть смогла обучиться классифицировать входные данные, которые представляют собой присутствие или отсутствие сигнала на каждом входном элементе. Таким образом, на выходе должно получаться значение логической функции «или», которая выводит значение 1 только тогда, когда хотя бы на одном входном элементе присутствует сигнал (значение 1), если все выходные элементы нулевые, то она выводит значение 0.

Если в системе будет только линейное преобразование, то подогнать соответствие входных данных к выходным будет невозможно, если только истинная зависимость не является линейной. Для того, чтобы можно было подгонять данные различных зависимостей, необходимы нелинейные преобразования. Мы будем использовать логистическую функцию, то есть сигмоиду.

Также для сигмоиды можно создать отдельный слой, чтобы использовать его в последовательном слое.

class Sigmoid(Layer):
    def __init__(self):
        Layer.__init__(self)

    def forward(self, inputs):
        return inputs.sigmoid()

Теперь создаем данные, модель и обучаем ее. На входе 2 признака, на выходе тоже два признака — это значения классов (класс 1 или класс 0).

# задача "логическое или", на выходе 2 класса
inputs = Tensor([[1, 0], [0, 0], [0, 1], [0, 0], [1, 1], [0, 0]])
targets = Tensor([[1, 0], [0, 1], [1, 0], [0, 1], [1, 0], [0, 1]])

model = Sequential([Linear(2, 3), Sigmoid(), Linear(3, 2), Sigmoid()])
optim = GradientDescent(parameters=model.get_parameters(), lr=20)
loss = MSELoss()

for epoch in range(20):
    outputs = model.forward(inputs)
    error = loss.forward(outputs, targets)
    print(f"epoch: {epoch}: {error}")
    error.backward()
    optim.step()

print(model.forward(inputs))

output:
epoch: 0: [[0.28494542944135637]]
...
epoch: 19: [[0.006474214203728644]]
[[0.8992398965992262, 0.0984163233128542],
[0.0722558994903615, 0.9280529331656421],
[0.9068566872731597, 0.09721210414491774],
[0.0722558994903615, 0.9280529331656421],
[0.9661878840588122, 0.0360237119005674],
[0.0722558994903615, 0.9280529331656421]]

Создаем входные данные, целевые данные и модель. Модель состоит из двух линейных слоев и сигмоидных функций активации. На первом слое 2 входных признака и 3 выходных, на втором — 3 входных и 1 выходной. Вычисляем ответ модели, создаем операнд функции ошибки и делаем от него обратное распространение. Затем обновляем значения всех обучаемых параметров (в этом примере все параметры обучаемые). После каждой итерацией обучения зануляем градиент.

Значение ошибки уменьшается, а выход приближается к целевому значению. То есть, например, последнее целевое значение — [0, 1], а выход модели на последний вход — [0.07, 0.92]. Это значит, что нейросеть обучается. Также значение функции ошибки уменьшилось с 0.28 до 0.006.

Как происходит обучение линейного слоя

Ниже нарисовал схематично как происходит вычисление производных для каждого слоя весов. Это происходит на основе цепного правила и правил дифференцирования, которые реализованы в обратном распространении в методе backward в классе Tensor.

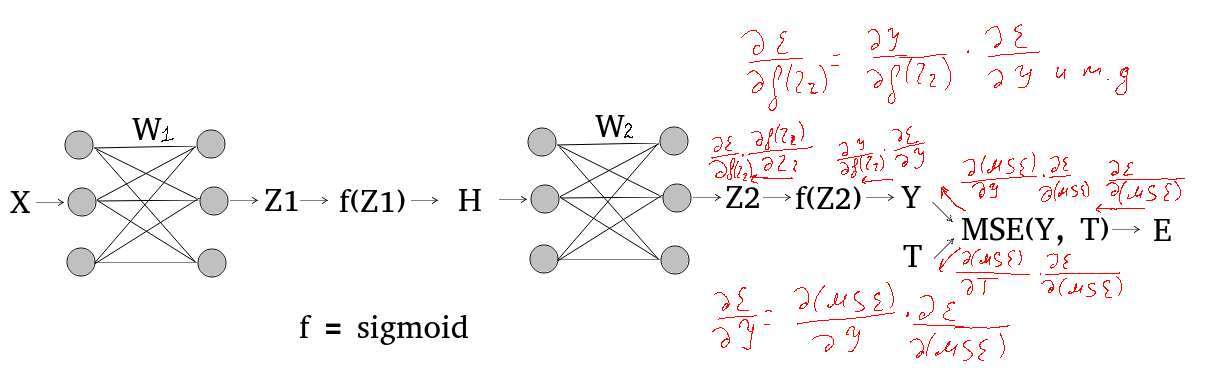
После инициализации весов происходит прямое распространение, то есть вычисление выходного значения каждого слоя. Выходное значение последнего слоя — это выходное значение всей нейросети в целом. На основе этого значения вычисляется значение функции ошибки, в данном случае, функции MSE.

После того, как получено значение этой функции, происходит обратное распространение — обратный проход по графу вычислений. Последовательно вычисляются градиенты во всех промежуточных значениях Z1, f(Z1), H и так далее.

После этого нужно изменить значения весов каждого линейного слоя на основе посчитанных в обратном проходе градиентов этих весов. Как они вычисляются я схематически показал красным цветом на рисунке выше. В статье про автоматическое дифференцирование есть ручной расчет того, как это все происходит.

Набор данных digits

Проверим на наборе данных digits. Судя по тому, как выглядят примеры, это одноканальные (черно-белые) изображения цифр, разрешения 8 на 8 пикселей, всего получается 64 входных признака (8*8).

Импортируем его из sklearn, берем первые 20 изображений и их метки как обучающие и 10 примеров как тестовые. Также понадобится импортировать созданные классы.

from sklearn import datasets
from linear import *
import numpy as np

digits = datasets.load_digits()

inputs = list(digits.data[:20] / 16)
labels = list(digits.target[:20])

test_inputs = list(digits.data[20:30] / 16)
test_labels = list(digits.target[20:30])

Делим входные значения на 16, чтобы все входные значения были в диапазоне от 0 до 1. Максимальное значение в наборе данных — 16, я узнал его с помощью функции np.max. Далее нужно преобразовать метки в выходные векторы признаков и входные данные представить в виде списка списков.

targets = zeros(shape=(20, 10))

for i in range(20):
    digit = labels[i]
    targets[i][digit] = 1

for i in range(len(inputs)):
    inputs[i] = list(inputs[i])

for i in range(len(test_inputs)):
    test_inputs[i] = list(test_inputs[i])

Создаем матрицу нулей размера 20 на 10, то есть 20 векторов по 10 признаков. Ставим единички в этой матрице в те места, которые соответствуют классам изображений. Всего 10 цифр, поэтому метка изображения соответствует цифре, которая на нем изображена. Превращаем входные массивы в списки, так как наши тензоры могут работать только со списками питона.

Теперь создаем тензоры входных и выходных данных, модель и обучаем ее.

inputs = Tensor(inputs)
test_inputs = Tensor(test_inputs)
targets = Tensor(targets)

model = Sequential([Linear(64, 32), Sigmoid(), Linear(32, 10), Sigmoid()])
optim = GradientDescent(parameters=model.get_parameters(), lr=2)
loss = MSELoss()

for epoch in range(200):
    outputs = model.forward(inputs)
    error = loss.forward(outputs, targets)
    print(f"epoch: {epoch}: {error}")
    error.backward()
    optim.step()

output:
epoch: 0: [[0.276185704091443]]
...
epoch: 199: [[0.06277212170659383]]

Проверяем модель на тестовых данных.

outputs = model.forward(test_inputs)
outputs = np.array(outputs.data)

for i in range(10):
    output_label = np.argmax(outputs[i])
    print(f"output_label: {output_label}, true_label: {test_labels[i]}")

output:
output_label: 0, true_label: 0
output_label: 1, true_label: 1
output_label: 2, true_label: 2
output_label: 8, true_label: 3
output_label: 4, true_label: 4
output_label: 8, true_label: 5
output_label: 6, true_label: 6
output_label: 7, true_label: 7
output_label: 8, true_label: 8
output_label: 9, true_label: 9

Здесь получаем ответ модели и приводим его в тип данных ndarray. Потом проходимся по каждому ответу и выбираем максимальное значение в векторе выходных признаков — это и есть ответ модели. Выводим полученные ответы модели и фактические значения меток к тестовым входным данным. Обучающие изображения сильно похожи на тестовые, поэтому модель может их легко классифицировать, но не все.

Применение линейных преобразований

Полносвязные слои (линейные) могут сталкиваться с некоторыми проблемами, особенно при работе с большими входными данными, такими как изображения.

Если входные данные имеют высокую размерность, например, изображения, количество параметров в полносвязном слое может быть очень большим, что приводит к увеличению времени обучения и, в целом, к переобучению — из-за большого количества параметров, полносвязные слои могут легко переобучаться, особенно если количество обучающих примеров мало.

В сверточных нейронных сетях (CNN) полносвязные слои часто используются после нескольких сверточных и пулинг слоев. После того, как сверточные слои извлекают признаки из изображения, данные преобразуются в одномерный вектор и передаются в полносвязные слои для классификации или регрессии. Это позволяет использовать мощность полносвязных слоев для принятия решений на основе извлеченных признаков.

Заключение

Мы рассмотрели процесс создания линейного слоя с нуля, а так же немного теории. Добавили некоторый новый функционал к этому мини-фреймворку для глубокого обучения. Попробовали этот фреймворк на наборе данных digits.

Тут есть непонятный момент, который заключается в том, что скорость обучения слишком большая (если сделать меньше 1, то сходиться будет очень долго, если вообще будет). Это возможно связано с инициализацией весов, чем больше веса, тем меньше скорость обучения и наоборот. А может из-за того, что нейросеть очень маленькая и задача очень простая. Но я так и не понял в чем причина, нормальное значение скорости обучения должно быть меньше единицы. В torch точно так же, так что градиенты вычисляются правильно. Есть идеи? — буду рад узнать, почему так происходит.

В папке с кодом есть дополнительный файл. В нем я показал как использовать тензоры torch для создания линейного слоя.

Папка с кодом на ГитХабе.

Канал в телеграме, файлы будут и там. В будущем планирую делать развивающие статьи по программированию и связанные с интеллектом. Также можете почитать уже имеющиеся статьи.