Долгая дорога к DiT (часть 3)

Заключительная (но ещё не последняя) статья из цикла про диффузные модели, где мы наконец отбросим примитивную модель из полносвязных слоёв и напишем работающий генератор изображений c архитектурой Diffusion Transformer (DiT). Разберёмся зачем нарезать изображения на квадратики и увидим, что произойдёт с вашей генерацией, если проигнорировать главную “слабость” трансформеров – неспособность понимать порядок.

• Часть 1

• Часть 2

Очень кратко про трансформеры

Перед тем как наконец написать код нашей финальной модели неплохо бы для начала понять, что такое модель-трансформер и для для чего она нужна. Много есть в интернете и статей на эту тему, и не менее полусотни видео на YouTube разной степени запутанности, но я хочу рассмотреть архитектуру трансформера с более практической стороны – не углубляясь далеко в детали и интерпретации. Давайте начнём с того, что вспомним как выглядит поток информации в той модели, которая получилась у нас в прошлый раз. Та модель получала на вход тензор с изображением, превращала его в скрытое представление (одномерный вектор с 600 элементами) и, прогоняя это скрытое представление через несколько DenoisingBlock’ов, выдавала на выход тензор той же размерности, что был получен на вход. Если забыть про первое батч-измерение, то получается, что в момент прохода данных через модель вся информация была представлена “всего лишь” единственным вектором – тензором с шейпом (600).

Но ведь информацию можно представить не только в виде единственного вектора. Запись человеческого голоса или музыкальную композицию логичнее было бы представить в виде некой последовательности векторов – есть начало, конец и “направление”. То же самое с текстом в LLM – токенизированный текст превращают в последовательность (sequence) векторов. В таких случаях тензор имеет шейп (N, C), где N – это количество элементов в последовательности, а C – размерность (величина) каждого элемента (вектора) в последовательности.

Тут важно сделать 2 замечания, касающихся информации, которая содержится в такой последовательности векторов.

• Во-первых, само расположение векторов в последова��ельности – это важная информация, терять которую никак нельзя. Если переставить ноты в музыкальном отрывке или слова в предложении, то смысл всего этой последовательности изменится. Это значит, что какая бы модель эти данные не обрабатывала бы она должна каким-то образом учитывать позицию каждого вектора в последовательности.

• Во-вторых, модель должна обработать всю информацию, которая содержится в последовательности – другими словами, не пропустить ни одного вектора. Да, знаю, звучит слишком очевидно, но давайте подумаем, как этого вообще можно сделать.

Представим, что наша задача – это создать модель, которая бы принимала на вход текст, превращённый в последовательность векторов, а на выходе бы выдавала скоринг – число в интервале [-1, 1], где минус единица означала бы резко негативное высказывание, ноль – нейтральное, а единица – позитивное. Sentiment analysis это ещё называют, классификатор текста, другими словами. И вот есть у нас на входе последовательность векторов – 3D тензор с шейпом (B, N, C). B – это измерение батча, но это мы уже знаем, а N, C – это матрица, где каждый столбец – это отдельный вектор в последовательности. Будем называть последовательность векторов, поступающую на вход модели матрица входных данных. Вот так бы выглядела матрица входных данных с шейпом (4, 7):

[]  []  []  []
[]  []  []  []
[]  []  []  []
[]  []  []  []
[]  []  []  []
[]  []  []  []
[]  []  []  []

4 вектора по 7 значений (числа) в каждом.

Ладно, в каком виде данные идут на вход понятно. Давайте теперь подумаем как можно обработать данные в этой матрице так, чтобы получить интересующее нас число (степень позитивности/негативности). Авторы рекуррентных нейронных сетей (RNN) решили обрабатывать каждый вектор последовательно аккумулируя данные в промежуточное представление. Совсем как функция reduce():

скрытое_представление_0 - это пустое_скрытое_представление.

rnn(скрытое_представление_0, вектор_1) = скрытое_представление_1
rnn(скрытое_представление_1, вектор_2) = скрытое_представление_2
...
rnn(скрытое_представление_n-1, вектор_n) = скрытое_представление_n

С таким подходом информация, хранящаяся во всех векторах будет учтена в итоговом результате. Таким образом, последнее скрытое представление будет (в теории) содержать всю информацию, нужную для классификации (анализ тональности текста, например).

А вот авторы трансформеров решили подойти к задаче по-другому. Идея трансформеров в том, чтобы прогнать матрицу исходных данные через нейросеть (трансформер-блок) целиком и на выходе получить такую же матрицу, но слегка изменённую. Если выражаться точнее, провести исходную матрицу через цепочку таких трансформер-блоков трансформируя её. В результата после серии трансформаций у нас получится матрица того же размера, что и матрица входных данных, но содержащая всю необходимую для классификации информацию в, допустим, последнем векторе. Вы наверное спросите “Почему достаточно последнего вектора? Информация из всех остальных векторов, что, каким-то образом перетекла в него?” Ответа: да, именно для этого и предназначен трансформер блок – он даёт возможность векторам в последовательности обмени��аться информацией (контекстуализироваться). Таким образом, условие “использовать данные всех векторов” обеспечивается тем, что, пройдя через цепочку трансформаций, каждый вектор “вберёт” в себя информацию всех остальных векторов в последовательности.

Не стоит сейчас сильно в это углубляться, поэтому запомните вот такие тезисы:

• Нейросеть (трансформер-блок) получает на вход матрицу (последовательность векторов)

• Внутри трансформер-блока происходит обмен информацией между векторами

• На выходе у трансформер-блока последовательность такого же размера, но вектора обогатились информацией из всех остальных векторов в последовательности

• Модель-трансформер состоит из цепочки таких трансформер-блоков

Возможно, я детальнее расскажу про работу трансформер-блока и механизм внимания, когда буду писать про то как современные Diffusion Transformers модели используют Relative Positional Bias и Rotary Positional Embeddings – для их работы надо вручную переписывать механизм внимания, поэтому придётся разбирать это всё достаточно глубоко. Но это в другой раз. Сейчас пора бы уже приступить к нашей финальной модели.

Создаём трансформер-блок

Возьмём за основу код, который получился у нас в предыдущей статье. Остановились мы вот на таком блоке:

class DenoiserBlock(nn.Module):  
    def __init__(self, hidden_dim, mlp_ratio, condition_dim):  
        super().__init__()  
        self.ln = nn.LayerNorm(hidden_dim)  
        self.mlp = nn.Sequential(  
            nn.Linear(hidden_dim, hidden_dim * mlp_ratio),  
            nn.SiLU(),  
            nn.Linear(hidden_dim * mlp_ratio, hidden_dim),  
        )  
        self.modulator_mlp = nn.Sequential(  
            nn.Linear(condition_dim, condition_dim * 4),  
            nn.SiLU(),  
            nn.Linear(condition_dim * 4, hidden_dim * 3),  
        )  
        nn.init.zeros_(self.modulator_mlp[-1].weight)  
        nn.init.zeros_(self.modulator_mlp[-1].bias)  
  
    def forward(self, x, c):  
        scale, shift, gate = self.modulator_mlp(c).chunk(3, dim=1)  
        z = self.ln(x)  
        z = z * (1 + scale) + shift  
        z = self.mlp(z)  
        z = z * gate  
        return z

Переименуем это класс в TransformerBlock и начнём превращать его в трансформер-блок. Для начала ещё раз взглянем на знакомую схему:

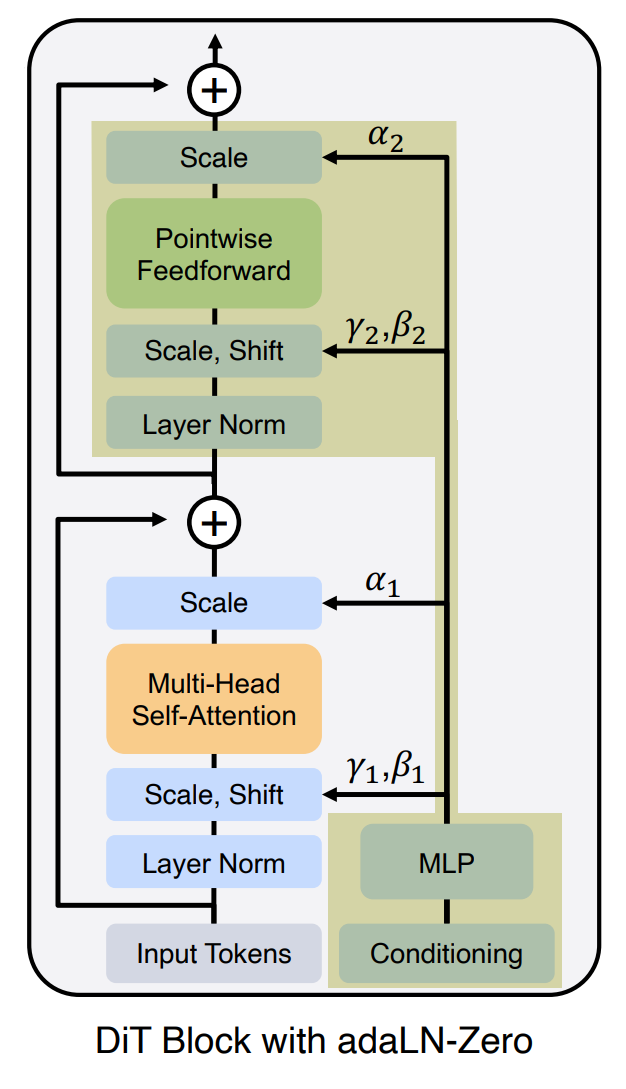
Может выглядит запутанно, но, вообще-то, большую часть этой схемы мы уже реализовали! Те части, которые я отметил зелёным – это, по сути, наш текущий код DenoiserBlock‘а. Pointwise Feedforward – это наше mlp. А MLP справа внизу – это то, что мы у нас зовётся modulator_mlp. Ладно, теперь понятно, что осталось сделать:

1. Добавить второй LayerNorm.

2. Сделать так, чтобы modulator_mlp возвращал 6 значений, а не 3 как сейчас.

3. Добавить Multi-Head Self-Attention – единственная новинка и сердце трансформера.

4. Соединить все слои, расставив в нужных местах skip-connections (плюсы на диаграмме)

Начнём по порядку. Вместо одного LayerNorm

self.ln = nn.LayerNorm(hidden_dim) 

Делаем два:

self.ln_1 = nn.LayerNorm(hidden_dim, elementwise_affine=False) 
self.ln_2 = nn.LayerNorm(hidden_dim, elementwise_affine=False) 

Тут elementwise_affine=False отключает у LayerNorm внутренние scale и shift (на самом деле, ещё в предыдущей статье стоило бы это сделать, но как-то совсем из головы вылетело). Scale и shift внутри LayerNorm нам не нужны, так как мы вручную это делаем через модуляцию.

Теперь настала очередь Модулятора:
Вот тут

self.modulator_mlp = nn.Sequential(  
    nn.Linear(condition_dim, condition_dim * 4),  
    nn.SiLU(),  
    nn.Linear(condition_dim * 4, hidden_dim * 3),  
)

Меняем 3 на 6 (и всё)

self.modulator_mlp = nn.Sequential(  
    nn.Linear(condition_dim, condition_dim * 4),  
    nn.SiLU(),
    nn.Linear(condition_dim * 4, hidden_dim * 6),  
)

А ещё переименуем self.mlp в self.ffn

Добавляем MultiheadAttention:

self.attn = nn.MultiheadAttention(
	embed_dim=hidden_dim,
	num_heads=num_heads,
	batch_first=True,  # это обязательно!
)

Это новый для нас блок, поэтому остановимся на нём поподробнее. Во-первых, принимает он на выход 3D-тензор с шейпом (B, N, C). Тут B – размер батча, это понятно. Потом идёт матрица (N, C) – N векторов каждый размером C элементов. А на выход получается тензор точно такого же шейпа, просто теперь каждый выходной вектор содержит “выжимку” от всех других векторов в последовательности. Но это ненужные сейчас детали, главное – это уяснить, что 3D-тензор на вход и такой же 3D тензор на выходе. Параметр embed_dim – это ожидаемый размер вектора (C). Количество векторов в последовательности N указывать не надо, так как nn.MultiheadAttention работает с последовательностями любой длины. Про смысл num_heads распишу подробнее в другой раз, скажу лишь, что это должно быть такое число, чтобы num_heads * 32 == embed_dims. А вот batch_first обязательно надо выставить в True. Если этого не сделать, то nn.MultiheadAttention будет ожидать, что на вход ему будут подавать тензор с шейпом (N, B, C). Это всё тяжелое наследие RNN, но помнить об этом надо, а то я однажды (при написании этой статьи) забыл написать batch_first=True у меня вся тренировка пошла насмарку.

Ладно, всё готов для последнего шага: переписать метод forward. Начинаем с модуляции

# Шейп x - (B, N, C). Шейп c - (B, Cond)
def forward(self, x, c):
	mod = self.modulator_mlp(c)  # (B, C * 6)
	mod = mod.unsqueeze(1)  # (B, 1, C * 6)
    scale_1, shift_1, gate_1, scale_2, shift_2, gate_2 = mod.chunk(6, dim=2)

Каждый scale, shift и gate имеет шейп (B, 1, C). Зачем нам дополнительное измерение посередине? Вспомните, что на вход у нас батч матриц – батч последовательностей векторов с шейпом (B, N, C). Наши модуляторы должны делать shift и scale каждого вектора в этих последовательностях. Но так как применятся они будут следующим образом:
x * scale или x + shift, то количество измерений у них должно совпадать, чтобы pytorch правильно произвёл broadcasting. Для этого и “лишнее” второе измерение.

Продолжаем по схеме выше:

def forward(self, x, c):
	mod = self.modulator_mlp(c)  # (B, C * 6)
	mod = mod.unsqueeze(1)  # (B, 1, C * 6)
    scale_1, shift_1, gate_1, scale_2, shift_2, gate_2 = mod.chunk(6, dim=2)

	z = self.ln1(x)  # LayerNorm 
	z = z * (1 - scale_1) + shift_1  # Scale, Shift
	z, _ = self.attn(z, z, z)  # Multi-Head Self-Attention
	z = z * gate_1  # На схеме Scale, а так это Gate
	x_after_attn = x + z  # Первый (+)

Результат очень похоже на то, что у нас уже было, только вместо MLP тут MultiheadAttention.

Давайте объясню про эту строку
z, _ = self.attn(z, z, z)

Зачем мы аж 3 раза отправляем наши данные в self.attn? Дело в том, что nn.MultiheadAttention может быть использована как для расчёта self-attention, когда векторы обмениваются информацией друг с другом, так и для cross-attention – когда векторы получают информацию из другой последовательности векторов. В таком случае вызов выглядел бы как-то так: self.attn(z, other_z, other_z). Не буду вдаваться в подробности что каждый аргумент значит, потому что не хочу поверхностно рассказывать про механизм внимания. Лучше дождитесь статьи про RoPE – там будет всё будет разобрано в деталях.
Помимо этого, заметили, что возвращается нам кортеж (tuple) из двух значений? Нам нужно только первое – это информация, которой векторы поделились друг с другом.

Добавляем последний кусок:

def forward(self, x, c):
	mod = self.modulator_mlp(c)  # (B, C * 6)
	mod = mod.unsqueeze(1)  # (B, 1, C * 6)
    scale_1, shift_1, gate_1, scale_2, shift_2, gate_2 = mod.chunk(6, dim=2)

	# Вектора обмениваются информацией.
	z = self.ln1(x)  # LayerNorm 
	z = z * (1 - scale_1) + shift_1  # Scale, Shift
	z, _ = self.attn(z, z, z)  # Multi-Head Self-Attention
	z = z * gate_1  # На схеме Scale, а так это Gate
	x_after_attn = x + z  # Первый (+)
	
	# Вектора "переваривают" полученную информацией. 
	z = self.ln2(x_after_attn)  # LayerNorm 
	z = z * (1 - scale_2) + shift_2  # Scale, Shift  
	z = self.ffn(z)  # Pointwise Feedforward
	z = z * gate_2  # На схеме Scale, а на деле Gate

	return x_after_attn + z  # Второй (+)

Выстроенные друг за другом такие TransformerBlockи (слои) представляют собой вот такую цепочку трансформаций:

Вектора обмениваются информацией
|
Вектора осваивают новую информацию
|
Вектора обмениваются информацией
|
Вектора осваивают новую информацию
|
Вектора обмениваются информацией
|
Вектора осваивают новую информацию
|
...

В общем-то, эта цепочка и есть трансформер, а TransformerBlock теперь выглядит вот так:

class TransformerBlock(nn.Module):  
    def __init__(self, hidden_dim, num_heads, mlp_ratio, condition_dim):  
        super().__init__()  
        self.ln1 = nn.LayerNorm(hidden_dim, elementwise_affine=False)  
        self.ln2 = nn.LayerNorm(hidden_dim, elementwise_affine=False)  
        self.attn = nn.MultiheadAttention(embed_dim=hidden_dim, num_heads=num_heads, batch_first=True)  
        self.ffn = nn.Sequential(  
            nn.Linear(hidden_dim, hidden_dim * mlp_ratio),  
            nn.SiLU(),  
            nn.Linear(hidden_dim * mlp_ratio, hidden_dim),  
        )  
        self.modulator_mlp = nn.Sequential(  
            nn.Linear(condition_dim, condition_dim * 4),  
            nn.SiLU(),  
            nn.Linear(condition_dim * 4, hidden_dim * 6),  
        )  
        nn.init.zeros_(self.modulator_mlp[-1].weight)  
        nn.init.zeros_(self.modulator_mlp[-1].bias)  
  
    def forward(self, x, c):  
        mod = self.modulator_mlp(c)  # (B, hidden_dim * 6)  
        mod = mod.unsqueeze(1)  # (B, 1, hidden_dim * 6)  
        scale_1, shift_1, gate_1, scale_2, shift_2, gate_2 = mod.chunk(6, dim=2)  
          
        z = self.ln1(x)  
        z = z * (1 - scale_1) + shift_1  
        z, _ = self.attn(z, z, z)  
        z = z * gate_1  
        x_after_attn = x + z  
  
        z = self.ln2(x_after_attn)  
        z = z * (1 - scale_2) + shift_2  
        z = self.ffn(z)  
        z = z * gate_2

        return x_after_attn + z

Основная модель

Теперь надо переделать основной класс Denoiser. Сейчас он выглядит вот так:

class Denoiser(nn.Module):  
    def __init__(self, hidden_dims, num_blocks, condition_dim):  
        super().__init__()  
  
        self.input_encoder = nn.Sequential(  
            nn.Flatten(start_dim=1),  
            nn.Linear(SIZE * SIZE, hidden_dims),  
        )  
        self.class_embeddings = nn.Embedding(num_classes, condition_dim)  
        self.class_mlp = nn.Sequential(  
            nn.Linear(condition_dim, condition_dim * 4),  
            nn.SiLU(),  
            nn.Linear(condition_dim * 4, condition_dim),  
        )
        block_list = [DenoiserBlock(hidden_dims, 4, condition_dim) for _ in range(num_blocks)]  
        self.blocks = nn.ModuleList(block_list)  
        self.output_decoder = nn.Sequential(  
            nn.Linear(hidden_dims, SIZE * SIZE),  
            nn.Unflatten(1, (1, SIZE, SIZE)),  
        )  
        self.time_linear = nn.Sequential(  
            nn.Linear(1, condition_dim),  
            nn.LayerNorm(condition_dim)  
        )  
  
    def forward(self, x, t, c):  
        hidden = self.input_encoder(x)  
        time_embedding = self.time_linear(t)  
        class_embedding = self.class_embeddings(c)  
        class_condition = self.class_mlp(class_embedding)  
        condition = time_embedding + class_condition  
        for block in self.blocks:  
            hidden = hidden + block(hidden, condition)  
        return self.output_decoder(hidden)

Первым дел��м добавляем в конструктор новый параметр num_heads:

def __init__(self, hidden_dims, num_heads, num_blocks, condition_dim):

И правим создание трансформер-блоков:

block_list = [TransformerBlock(hidden_dims, num_heads, 4, condition_dim) for _ in range(num_blocks)]

А вот с input_encoderом будет сложнее. Напоминаю, Diffusion Transformer работает с последовательностью векторов – тензор шейпом (B, N, C). А вот на вход модели будет подаваться тензор чёрно-белого изображений с шейпом (B, 1, 24, 24). Чтобы вообще запустить наш трансформер, входной тензор надо превратить в последовательность векторов. Для этого воспользуемся давно отработанным (ещё со времён Visual Transformers) приёмом.

Идея простая:

1. Разбить наше изображение на несколько кусков (патчей):

   

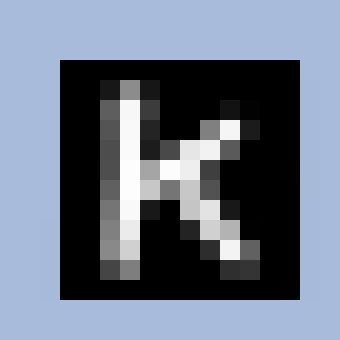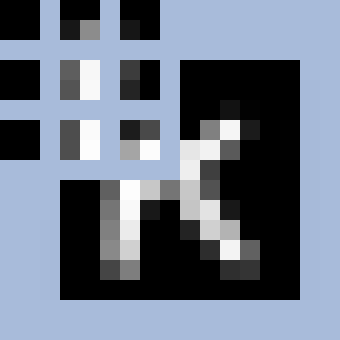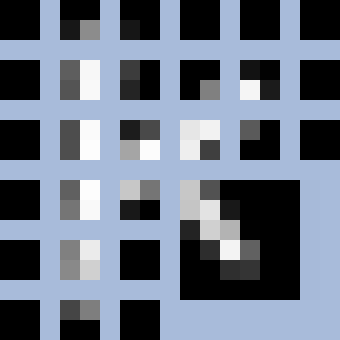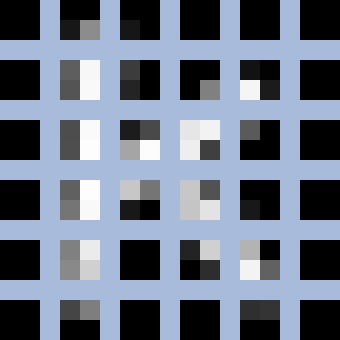
2. Из каждого патча (в нашем случае это маленькая матрица 2×2) сформировать вектор длиной 4. Превратить двумерный тензор в одномерный, другими словами. А потом объединить эти вектора в последовательность.

3. С помощью nn.Linear(4, hidden_dim) спроецировать каждый вектор пикселей в вектор скрытого представления. И получится у нас как раз нужный нам вектор (B, N, C), где N – это количество патчей (в нашем случае (24 / 2) * (24 / 2) == 144), а C – размерность вектора скрытого представления hiddent_dim.

Попробуем это реализовать в коде. Для “нарезки” тензора изображения на прямоугольные патчи в PyTorch уже есть готовый класс nn.Unfold. А работает он вот так:

# Код для примера
unfold = nn.Unfold(kernel_size=2, stride=2)
# Шейп переменной x - (B, 1, 24, 24)
y = unfold(x)
# Шейп переменной y - (B, 1*4, 24/2 * 24/2) == (B, 4, 144)

another_unfold = nn.Unfold(kernel_size=3, stride=3)
z = y = another_unfold(x)
# Шейп переменной z - (B, 1*9, 24/3 * 24/3) == (B, 9, 64)

Здесь nn.Unfold(kernel_size=2, stride=2) нарежет входной тензор изображения на патчи 2×2 и объединит два пространственных измерения в одно. Правда, вернёт он нам тензор с шейпом (B, pixel_vector_size, N), где последнее измерение – это длина последовательности. А нам надо, чтобы длина последовательности была вторым измерением. Для этого есть функция permute:

# x.shape == (B, 4, 144)
y = x.permute(0, 2, 1)  # меняем местами второе и третье измерения
# x.shape == (B, 144, 4)

После этого останется лишь проецировать вектор длиной 4 на вектор длиной hidden_dim. Тут всё просто через обычный nn.Linear(4, hidden_dim). Вот так это всё будет выглядеть в нашем классе:

Вместо

self.input_encoder = nn.Sequential(  
    nn.Flatten(start_dim=1),  
    nn.Linear(SIZE * SIZE, hidden_dims),  
)

Делаем

self.input_patcher = nn.Unfold(kernel_size=2, stride=2)
self.input_projector = nn.Linear(4, hidden_dims)

А внутри метода forward заменяем

hidden = self.input_encoder(x)

на

input_patches = self.input_patcher(x)
input_seq = input_patches.permute(0, 2, 1)
hidden = self.input_projector(input_seq)

С input_encoderом разобрались, теперь надо также адаптировать ouput_encoder. Он должен будет превращать последовательность векторов обратно в одноканальное (чёрно-белое) изображение. Хорошо, что в PyTorch уже есть класс “обратный” nn.Unfold – это nn.Fold:

# Код для примера
fold = nn.Fold(output_size=(SIZE, SIZE), kernel_size=2, stride=2)

# x.shape == (B, hidden_dims, 144)
y = fold(x)
# y.shape == (B, hidden_dims/4, SIZE, SIZE)

Только тут одна загвоздка – nn.Fold хоть и сливает патчи в тензор изображения, число каналов при этом будет четверть от hidden_dims. А нам надо чтобы число каналов было 1. А так как hidden_dims явно побольше 4-х будет, то нам надо либо уменьшить число каналов до операции Fold, либо сделать это уже после Fold’a, обработав тензор изображения через свёрточную сеть. На самом деле так и поступим:

nn.Conv2d(in_channels=hidden_dims/4, out_channels=1, kernel_size=3, padding=1)

Про свёрточные сети и nn.Conv2d прочитайте где-нибудь отдельно. Хоть в документации PyTorch. Если я ещё их начну объяснять, то и так уже большая статья окончательно все берега потеряет. А так эта операция просто сделает из тензора с шейпом (B, hidden_dims/4, 24, 24) тензор одноканального изображения (B, 1, 24, 24) – именно то, что нам и нужно.

Меняем код. Теперь вместо

self.output_decoder = nn.Sequential(  
    nn.Linear(hidden_dims, SIZE * SIZE),  
    nn.Unflatten(1, (1, SIZE, SIZE)),  
)

Пишем

self.output_decoder = nn.Sequential(  
    nn.Fold(output_size=(SIZE, SIZE), kernel_size=2, stride=2),  
    nn.Conv2d(in_channels=hidden_dims//4, out_channels=1, kernel_size=3, padding=1),  
)

А в самом конце метода forward

return self.output_decoder(hidden)

Заменяем на

output_seq = hidden.permute(0, 2, 1)  
return self.output_decoder(output_seq)

class Denoiser(nn.Module):  
    def __init__(self, hidden_dims, num_heads, num_blocks, condition_dim):  
        super().__init__()  
  
        self.input_patcher = nn.Unfold(kernel_size=2, stride=2)  
        self.input_projector = nn.Linear(4, hidden_dims)  
        self.class_embeddings = nn.Embedding(num_classes, condition_dim)  
        self.class_mlp = nn.Sequential(  
            nn.Linear(condition_dim, condition_dim * 4),  
            nn.SiLU(),  
            nn.Linear(condition_dim * 4, condition_dim),  
        )  
        block_list = [TransformerBlock(hidden_dims, num_heads, 4, condition_dim) for _ in range(num_blocks)]  
        self.blocks = nn.ModuleList(block_list)  
        self.output_decoder = nn.Sequential(  
            nn.Fold(output_size=(SIZE, SIZE), kernel_size=2, stride=2),  
            nn.Conv2d(in_channels=hidden_dims//4, out_channels=1, kernel_size=3, padding=1),  
        )  
        self.time_linear = nn.Sequential(  
            nn.Linear(1, condition_dim),  
            nn.LayerNorm(condition_dim)  
        )  
  
    def forward(self, x, t, c):  
        input_patches = self.input_patcher(x)  
        input_seq = input_patches.permute(0, 2, 1)  
        hidden = self.input_projector(input_seq)  
  
        time_embedding = self.time_linear(t)
        class_embedding = self.class_embeddings(c)  
        class_condition = self.class_mlp(class_embedding)  
        condition = time_embedding + class_condition  
        for block in self.blocks:  
            # теперь мы просто передаём результат работы одного блока
            # на вход другому блоку
            hidden = block(hidden, condition)  
  
        output_seq = hidden.permute(0, 2, 1)  
        return self.output_decoder(output_seq)

Можно приступить к обучению, но сначала надо внести несколько изменений в код тренировки.

Там где мы определяем subset надо вместо

subset = Subset(dataset, torch.randperm(4096 * 2))

написать

subset = dataset

Будем использовать для обучения не срез из 9 тысяч сэмплов, а весь датасет из 112 тысяч. Потому что Diffusion Transformer слишком уж хорошо обучается по сравнению с предыдущей нашей моделью и запросто может осилить обучающий набор такого размера.

Теперь инициализация модели:

model = Denoiser(hidden_dims=16*8, num_heads=8, num_blocks=8, condition_dim=32)

Я тут немного перегнул с количеством голов, можно обойтись и меньшим количеством. А длина вектора получается 128, это означает, что наше скрытое представление – это матрица (144, 128) – последовательность из 144 векторов каждый размеров 128. Заметьте, что размер скрытого представления в DiT модели намного больше – 144 x 128 == 18432 элементов в матрице, против вектора 600 элементами из нашей предыдущей модели, при том что сама DiT-модель меньше раза в 3 и работает лучше, но это я забегаю вперёд.

Осталось лишь задать гиперпараметры:

BATCH_SIZE = 128  
LR = 6e-4  
DEVICE = 'cuda'  
EPOCHS = 10

EPOCHS поменьше, потому что обучающий набор теперь больше. Всё готово к тренировке, запускаем и..

Вот так да! Не работает.

Дело в том, что написанный нами трансформер полностью игнорирует критически важную часть информации, которая содержится во входной матрице данных – информацию о расположении векторов в последовательности. Сейчас поясню на простом примере. Допустим, у нас есть вот такая последовательность из 4-х векторов:

[1]  [8]  [2]  [0]
[1]  [6]  [3]  [1]
[5]  [8]  [6]  [5]

Вспоминаем, что наш трансформер – это просто цепочки чередующихся MHA (Multi-Head Attention) и FNN (Feedforward Network) слоёв, где FNN работает на уровне отдельных векторов. Что я имею ввиду? Для матрицы с шейпом (4, 3) как здесь FNN слой выглядел бы вот так:

nn.Sequential(
	nn.Linear(3, 12),
	nn.SiLU(),
	nn.Linear(12, 3),
)

Этот слой обрабатывает каждый из 4-х векторов независимо друг от друга, даже параллельно я скажу. Как и задумано, ведь для обмена информацией между векторами у нас есть MHA слои. И вот тут то и вылезает наша проблема – механизм Attention сам по себе никак не учитывает порядок векторов в последовательности. Другими словами, если бы мы поменяли местами вектора в последовательности, то результат работы MHA-слоя для каждого вектора не изменился бы:

      до MHA                       до MHA

[1]  [8]  [2]  [0]           [8]  [2]  [0]  [1]
[1]  [6]  [3]  [1]           [6]  [3]  [1]  [1]
[5]  [8]  [6]  [5]           [8]  [6]  [5]  [5]
        
     после MHA                    после MHA
		 
[0]  [1]  [0]  [0]           [1]  [0]  [0]  [0]
[1]  [0]  [1]  [0]           [0]  [1]  [0]  [1]
[2]  [0]  [1]  [2]	   	     [0]  [1]  [2]  [2]

А раз перестановка векторов местами не влияет на то, какую информацию получит каждый вектор после прохода через MHA-слой (а это единственное место, где отдельный вектор может как-то что-то узнать о том, что помимо него в последовательности вообще есть другие несущие информацию вектора), то для нашего трансформера все вот эти входные изображению будут “выглядеть” совершенно идентично:

Из-за этого всё обучение модели идёт насмарку. Но выход есть!

На самом деле, есть несколько способов внедрить в модель информацию о позиции векторов в последовательности. Вот только чтобы реализовать наиболее продвинутые “техники” такие как Relative Positional Bias или ставший уже повсеместными RoPE надо переопределять механизм внимания. Эти темы мы разберём в следующих статьях, а сейчас решим проблему самым простым способом – через Absolute Positional Embeddings.

Работать это будет следующим образом: как только мы формируем матрицу входных данных (последовательность векторов) из изображения, поданного методу forward, надо к этой матрице прибавить матрицу (тензор) такого же размера. В этой матрице и будет содержаться информация о том, какую позицию занимает вектор в последовательности. И так как эта матрица всё время будет одна и так же, модель, а точнее трансформер-блоки научатся “вычленять” эту информацию из переданной им последовательности векторов. Словами не так понятно выходит, поэтому смотрим на код:

# Сразу после
hidden = self.input_projector(input_seq)
# Прибавляем матрицу (pos_embeddings)
hidden = hidden + self.pos_embeddings * self.pos_embeddings_scale

А self.pos_embeddings и self.pos_embeddings_scale определяем в конструкторе:

self.pos_embeddings = nn.Parameter(data=torch.randn(144, hidden_dims))  
self.pos_embeddings_scale = nn.Parameter(torch.zeros(1))

torch.randn(144, hidden_dims) создаст тензор совпадающий по форме с нашей последовательностью векторов, тут понятно. А nn.Parameter нужен для того, чтобы во время обучения наша DiT модель могла адаптировать (выучить) матрицу positional embeddings. Можно было бы оставить pos_embeddings как статичный тензор, но тогда бы torch.randn не подошёл бы. Идём дальше. Уже догадались для чего нужен self.pos_embeddings_scale? Это тоже обучающийся тензор из одного единственного значения, а инициализируется он нулём для того, чтобы в начале обучения исключить влияние self.pos_embeddings на hidden. Если этого не сделать, то hidden буквально потонет в шуме и первые шаги тренировки будут очень нестабильными. Нет, конечно, потом все градиенты выровняются, но какой-то ресурс тренировки будет потерян. В общем, это просто способ немного ускорить тренировку.

Ладно, теперь всё готово для следующей попытки. И на этот раз получилось гораздо лучше:

Уже на 6-й эпохе модель обучилась всем 47 классам.

А теперь сравним, что выдаст нам модель из предыдущей статьи, если тоже тренировать её на всём датасете:

Результат полносвязной модели

Вот здесь финальная версия кода

Что дальше?

Вы думаете, что написали мы модель и всё на этом? Как раз наоборот, сейчас на руках у нас прототип Diffusion Transformer’a – идеальный “модельный организм”, на котором можно продолжать экспериментировать добавляя фичи “взрослых” моделей.

Первое, что приходит в голову – это заменить имеющийся Absolute Positional Embeddings чем-то более современным, но сразу же бросаться имплементировать популярный Rotary Positional Embeddings (RoPE) будет слишком сложно, поэтому стоит начать с чего-то попроще, а конкретно с Relative Positional Bias, на примере которого разобрать и сам механизм внимания (сердце трансформера) и наглядно показать, каким образом можно модифицировать этот механизм, чтобы модель воспринимала информацию о взаимном расположении векторов в последовательности.

В следующих статьях я подробно разберу механизм внимания и расскажу о современных способах внедрить в модель информацию о взаимном расположении векторов, а также попробуем создать Autoregressive Transformer, который будет генерить нам изображения токен за токеном совсем как GPT. Продолжение следует.

Бонус. Анимация инференса в 40 шагов: