В предыдущих частях (первая, вторая) описан мой опыт обучения простого искусственного нейрона бинарной классификации и размышления об этом. В этой статье я продолжаю размышления и вношу соответствующие корректировки в код.
В предыдущей версии мне не нравится, что в процедуре обучения есть оператор сравнения if. Он применяется, когда вывод сравнивается с меткой класса (if not compare(x,y):), и если вывод и метка класса не равны, то происходит коррекция веса. Мне хочется “более чистой” математики и не применять операторы сравнения, если этого можно избежать..
Убираем оператор сравнения в формуле расчета коррекции
В данном случае избежать операторов сравнения можно и достаточно легко.
Коррекция веса происходит по формуле: w[index] =w[index] + y*lmd*x[index], где y – метка класса соответствующего объекта. Если заменить y на на разницу между меткой класса и выводом (y – onestep(neuron.output(x)) и убрать оператор сравнения, то это и будет решением.
Рассмотрим, почему это так.
Метка класса (y) равна или +1 или -1. А вывод равен также или +1 или -1. Соответственно если вывод и метка класса равны, то разница между выводом и меткой класса равна нулю. А если вывод и метка класса не равны, то разница (y – onestep(neuron.output(x)) будет равна или +2 или -2. Получается, что коррекция делается на каждой итерации, но при равенстве вывода и метки класса коррекция равна нулю, что равносильно тому, как если бы она не происходила, как и в предыдущей версии. Далее мы можем домножить величину коррекции на 1/2, чтобы вернуться к 1 и к прошлым форматам, и учесть это в размере lmd, либо оставить lmd как и было, так как уменьшение lmd в два раза в данном случае не принципиально на уровне формул – lmd так и так является параметром подбора.
Таким образом убираем оператор сравнения и коррекция весов теперь происходит на каждой итерации:
error = y - onestep(neuron.output(x))
w[index] = w[index] + error*lmd*x[index] Интересно, что таким ходом мы приходим к распространенной формуле, часто называемой “дельта-правило”.
Убираем оператор сравнения в функции качества
Необходимо отметить, что этот же оператор сравнения есть в функции качества.
Код функции качества в предыдущей версии выглядит так:
# Функция качества. Считает количество объектов с ошиибкой.
def Q():
return sum([1 for index, x in enumerate(x_train) if not compare(x,y_train[index])])Здесь тоже хочется избежать применения оператора сравнения, и для этого применим похожий способ.
Будем суммировать не 1 в случае несовпадения вывода с меткой класса, а непосредственно величины разницы, да еще возведенные в квадрат для устранения влияния знака.
Соответственно, если вывод и метка класса равны, то разница равна нулю, и к итоговой сумме ничего не прибавляется. Если же вывод и метка класса не равны, то разница равна или +2 или -2, и к общей сумме прибавляется 4.
Новый код функции качества получается таким:
# Функция качества. Считает количество объектов с ошиибкой.
def Q():
return sum ([((y_train[index] - onestep(neuron.output(x)))**2) for index, x in enumerate(x_train) ])Если добавить деление итоговой суммы на 4, то получим количество ошибочно классифицируемых объектов. Но в данном случае не принципиально – применять sum или sum/4, так как обучение прекращается, когда Q() = 0, а для sum и sum/4 это совпадает.
Итоговый код с изменениями
В итоге получили новый код с более чистой математикой.
Код для исходных данных
import numpy as np
import matplotlib.pyplot as plt
# исходные данные
x_train = np.array([[10, 50], [20, 30], [25, 30], [20, 60], [15, 70], [40, 40], [30, 45], [20, 45], [40, 30], [7, 35]])
y_train = np.array([-1, 1, 1, -1, -1, 1, 1, -1, 1, -1])
# формируем множества по меткам
x_0 = x_train[y_train == 1]
x_1 = x_train[y_train == -1]
# создаем изображение
plt.xlim([0, max(x_train[:, 0]) + 10])
plt.ylim([0, max(x_train[:, 1]) + 10])
plt.scatter(x_0[:, 0], x_0[:, 1], color='blue')
plt.scatter(x_1[:, 0], x_1[:, 1], color='red')
plt.ylabel("длина")
plt.xlabel("ширина")
plt.grid(True)
plt.show()Код создания класса Neuron и определения функций
class Neuron:
def __init__(self, w): # Действия при создании класса
self.w = w
def output(self, x): # Сумматор
return np.dot(self.w, x) # Суммируем входы
# Функция активации - Функция единого скачка
def onestep(x):
return 1 if x >= 0 else -1
# Функция качества.
def Q():
return sum ([((y_train[index] - onestep(neuron.output(x)))**2 ) for index, x in enumerate(x_train)])
# Функция добавления размерности
def add_axis(source_array, value):
this_array = []
for x in source_array: this_array.append(np.append(x, value))
return np.array(this_array)
# добавляем фикированное значение (1)
x_train = add_axis(x_train, 1)Код обучения
import random
# Случайный выбор для коэффициентов
def random_w():
return round((random.random() * 10 - 5),1)
N = 500 # максимальное число итераций
lmd = 0.01 # шаг изменения веса
w_history = [] # Массив для сохранения истории
# Инициируем веса случайным образом
w = np.array([random_w(), random_w(), random_w()])
w_history.append(np.array(w)) # сохранякем историю
neuron = Neuron(w)
# Считаем качество
Q_current = Q()
# проходим итерации
for n in range(N):
if Q_current == 0: break
# Выбираем случайным образом объект
random_index = random.randint(0,len(x_train)-1)
x = x_train[random_index]
y = y_train[random_index]
# выбираем вес случайным образом
index = random.randint(0,len(w)-1)
# Вместо метки класса применяем величину отклонения
error = y - onestep(neuron.output(x)) # считаем величину отклонения (!)
w[index] = round(w[index] + error*lmd*x[index],4) # коррекция веса с учетом параметров данных и величины отклонения (!)
w_history.append(np.array(w)) # сохранякем историю
#neuron = Neuron(w)
neuron.w = w
Q_current = Q()
if Q_current == 0: break
print(w)
print('Q_current:', Q_current, 'n:', n)Если добавить печать промежуточных результатов, то можно видеть историю коррекций – веса и количества ошибочно классифицированных объектов.
[-0.1 -3.9 -2.4] 5.0
0 [-0.1 -3.9 -2.4] 5.0
1 [-0.1 -3.9 -2.38] 5.0
2 [-0.1 -3.9 -2.38] 5.0
3 [ 0.7 -3.9 -2.38] 5.0
4 [ 0.7 -3.3 -2.38] 5.0
5 [ 0.7 -3.3 -2.38] 5.0
6 [ 0.7 -3.3 -2.38] 5.0
7 [ 0.7 -3.3 -2.36] 5.0
8 [ 0.7 -3.3 -2.36] 5.0
9 [ 0.7 -3.3 -2.36] 5.0
10 [ 0.7 -3.3 -2.36] 5.0
11 [ 0.7 -3.3 -2.34] 5.0
12 [ 0.7 -2.4 -2.34] 5.0
13 [ 1.5 -2.4 -2.34] 5.0
14 [ 1.5 -2.4 -2.34] 5.0
15 [ 1.5 -2.4 -2.32] 5.0
16 [ 1.5 -2.4 -2.32] 5.0
17 [ 2.3 -2.4 -2.32] 4.0
18 [ 2.3 -2.4 -2.32] 4.0
19 [ 2.3 -2.4 -2.32] 4.0
20 [ 2.3 -1.8 -2.32] 2.0
21 [ 2.9 -1.8 -2.32] 0.0
[ 2.9 -1.8 -2.32]
Q_current: 0.0 n: 21
Визуально на графике это выглядит так:
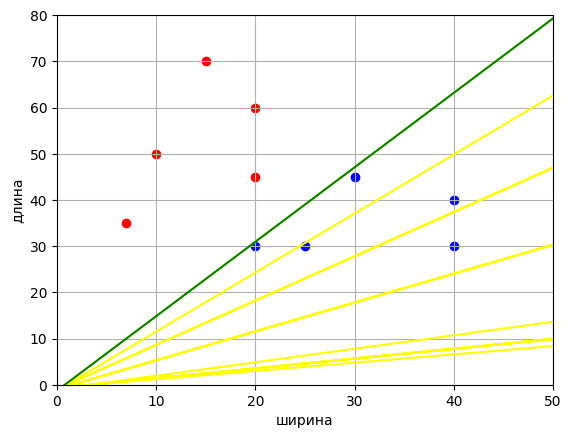
Код создания изображения
# создаем изображение
# Рисование линии
def draw_line(x,w,color):
if w[1]:
line_x = [min(x[:, 0]) - 10, max(x[:, 0]) + 10]
line_y = [-w[0]/w[1]*x - w[2]/w[1] for x in line_x]
plt.plot(line_x, line_y, color=color)
else:
print('w1 = 0')
plt.xlim([0, max(x_train[:, 0]) + 10])
plt.ylim([0, max(x_train[:, 1]) + 10])
plt.scatter(x_0[:, 0], x_0[:, 1], color='blue')
plt.scatter(x_1[:, 0], x_1[:, 1], color='red')
for index, key in enumerate(w_history):
if index:
draw_line(x_train, key, 'yellow')
else:
draw_line(x_train, key, 'grey')
draw_line(x_train, w, 'green')
plt.ylabel("длина")
plt.xlabel("ширина")
plt.grid(True)
plt.show()
if w[1]:
print('y = ' + str(round(-w[0]/w[1],4)) + 'x + ' + str(round(-w[2]/w[1],4)))
else:
print('x = 0')Примечание
Если заметили какие-либо неточности или явные нестыковки – пожалуйста, отметьте это в комментариях.

Автор: AnatolyBelov


