Прочтите эту историю о человеке, создавшем ИИ, прежде чем она обойдётся вам так же дорого, как ему.

В 1943 году идея машины, способной мыслить, показалась бы абсурдной.
Но одна концепция того года зажгла фитиль всего, что мы сейчас называем искусственным интеллектом.
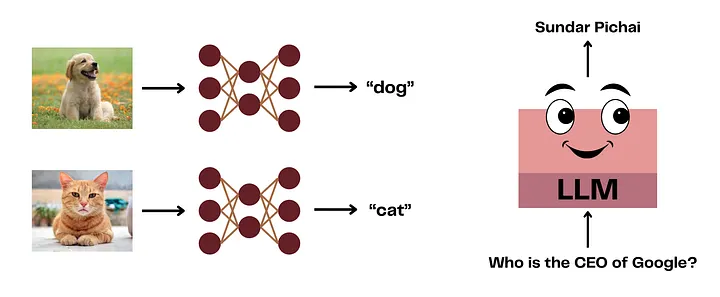
Два молодых учёных в 1943 году вовсе не пытались создать разумные машины. Они преследовали куда более амбициозную цель:
идеальную модель мозга.
Это стремление привело к созданию первого искусственного нейрона – идеи, на которой до сих пор держится весь ИИ. Но оно же уничтожило одного из её создателей.
Он умер в безвестности, убеждённый, что его работа провалилась, потому что не была идеальной.
Это история той ошибки и того, почему она до сих пор отнимает у людей годы жизни.
Невероятное партнёрство
Давайте вернёмся в 1943 год.
Уолтеру Питтсу было 18 лет, и за плечами у него было тяжёлое детство.
Он сбежал из дома и проводил большую часть времени, прячась в библиотеках от хулиганов.
Но, честно говоря, он был исключительно одарённым. К 16 годам он читал сложные книги по математической логике, которые большинство взрослых не смогли бы понять.
Однажды он встретил Уоррена Маккалока, нейробиолога на 25 лет старше его.
Вместе они поставили перед собой смелую цель: доказать, что мозг, несмотря на всю его биологическую сложность, по сути является всего лишь булевой схемой.
Каждый нейрон, как они полагали, выполняет простые логические операции вроде операций AND и OR, знакомых вам по программированию.

Что вдохновило эту идею?
К 1940-м годам учёные уже десятилетиями изучали нейроны на клеточном уровне.
Они обнаружили нечто удивительное: нейроны вели себя по принципу «всё или ничего».
Входные сигналы суммировались, и если они превышали определённый порог, нейрон испускал импульс. Если нет – ничего не происходило. Бинарно. 0 или 1.
Учёные, например, те, кто изучал гигантский нейрон кальмара (да, такое действительно существует), подавали электрическое напряжение непосредственно на нейроны и наблюдали за результатом.
Входные сигналы, называемые пресинаптическими потенциалами, сначала выглядели аналоговыми. Но выходной сигнал всегда был бинарным.
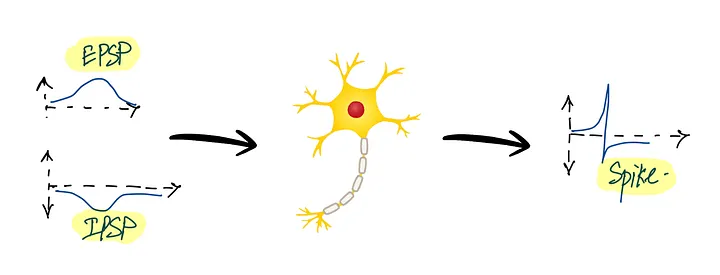
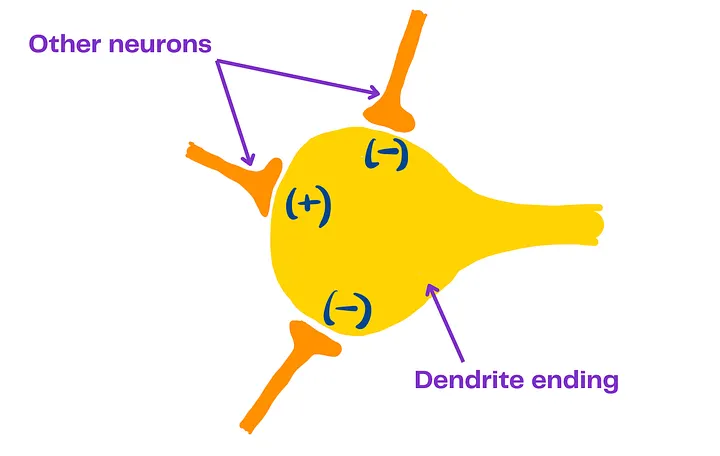
Возбуждающие сигналы – это положительные сигналы (EPSP), а тормозящие – отрицательные.
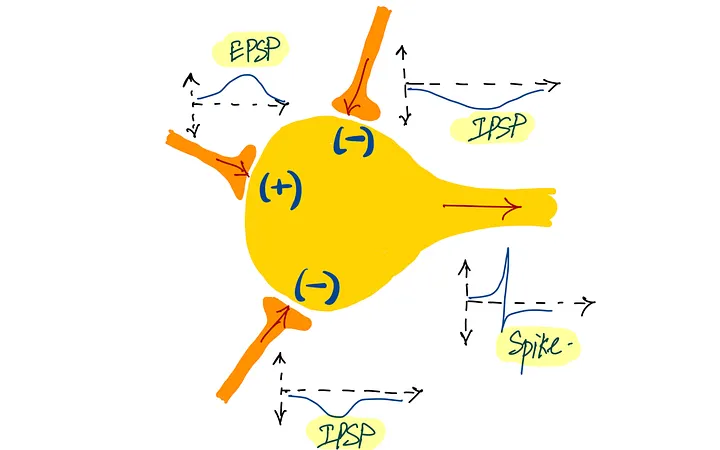
Выходной сигнал всегда бинарный. Он либо выдаёт импульс, либо нет.
Это поведение «включено-выключено» напомнило Питтсу то, о чём он читал: булеву логику.
Что такое булева логика?
Прежде чем продолжить, давайте разберёмся, что такое булева логика на самом деле.
Булева логика оперирует значениями истина и ложь – или единицами и нулями. Всего два числа, способные представить всё что угодно.
Допустим, у вас есть простое условие: x == 2. Это означает «равен ли x двум?» Если да, оно оценивается как истина. Если нет – как ложь.
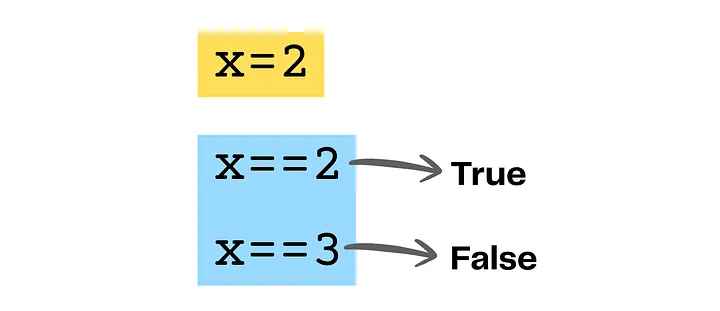
Теперь вы можете комбинировать эти условия с помощью операторов.
Оператор OR: Если вы говорите x == 2 OR y == 3, общее условие истинно, если выполняется хотя бы одно из двух условий. Это как сказать «я держу яблоко или апельсин» – вам нужно держать что-то одно, чтобы это было истиной.
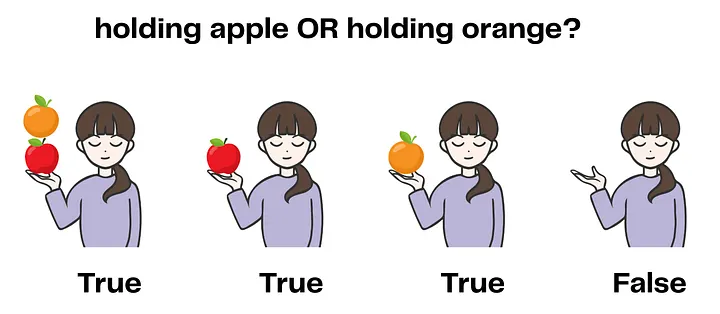
Оператор AND: Если вы говорите x == 2 AND y == 3, оба условия должны быть истинны. Это как сказать «я держу яблоко и апельсин» – вам нужно держать и то, и другое.
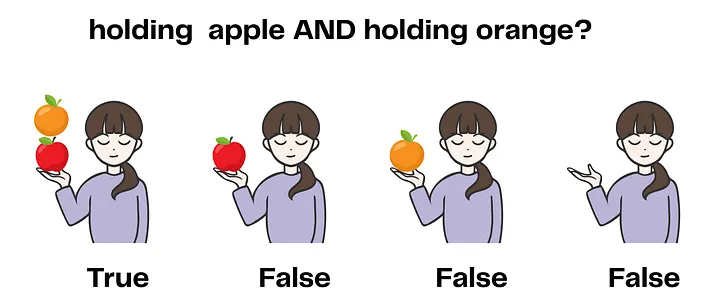
Утверждение истинно только если девушка держит и яблоко, и апельсин
Суммируя все возможные результаты:
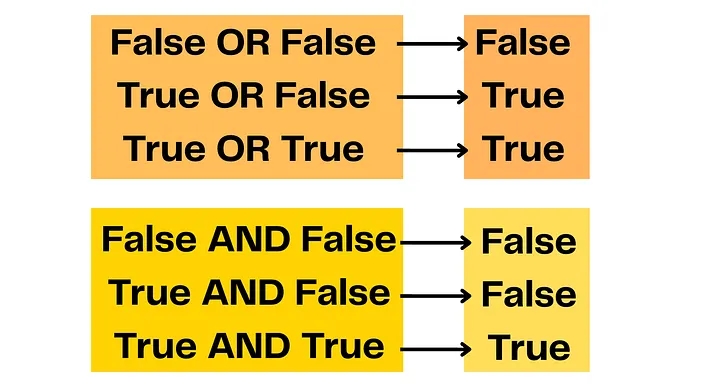
Эти простые операции – основа всех вычислений.
Нейрон Маккалока-Питтса
Маккалок и Питтс хотели создать искусственный «нейрон», способный имитировать эти логические операции.
Любой нейрон Маккалока-Питтса выглядит при��ерно так.
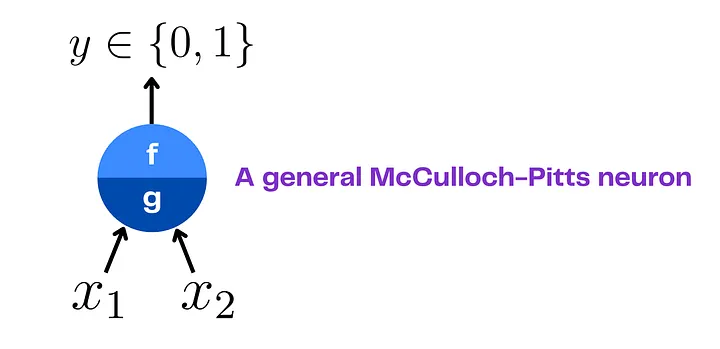
Есть несколько входов, а выход – булево значение (либо 0, либо 1).
Есть две внутренние функции:
-
g, которая используется для объединения входов определённым образом
-
f, которая используется для преобразования комбинации в бинарный 0 или 1 для вывода как y
Как же представить обычные логические операции в виде нейронов?
Начнём с логической операции OR. Мы можем представить её в виде таблицы:
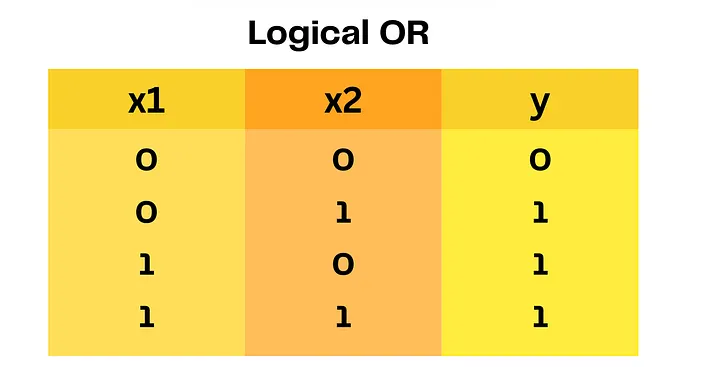
Чтобы построить нейрон, имитирующий это, нам нужны две функции:
-
g(x): Объединяет входы вместе
-
f(x): Определяет выход на основе комбинации
Для операции OR всё просто.
Пусть g(x) = x1 + x2 (просто суммируем входы). И пусть f(x) = 1, если g > 0, иначе f(x) = 0.
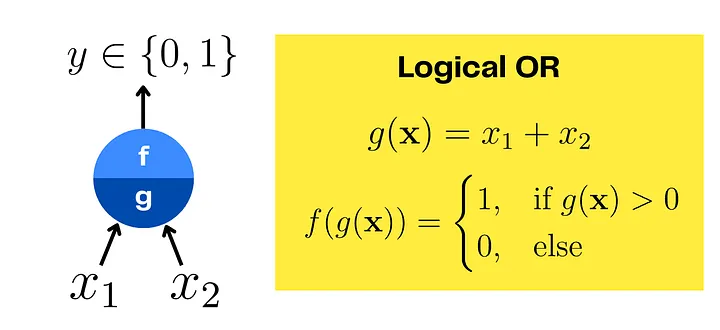
Попробуйте.
Если x1 = 0 и x2 = 1, то g = 1, следовательно f = 1. Если x1 = 0 и x2 = 0, то g = 0, следовательно f = 0. Работает!
Аналогично, операция AND может быть представлена так:
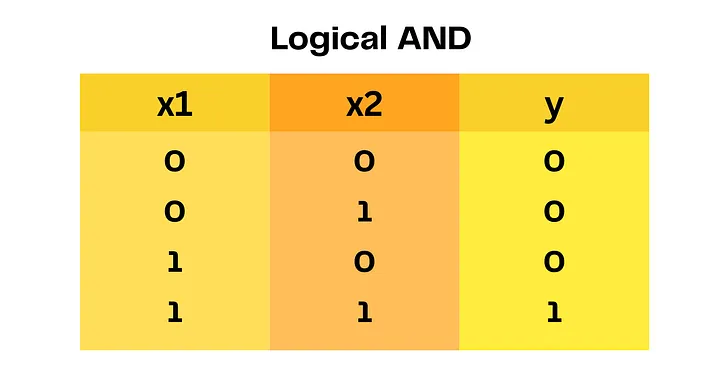
Здесь g(x) = x1 + x2 (как и раньше). Но теперь f(x) = 1, если g = 2, иначе f(x) = 0.
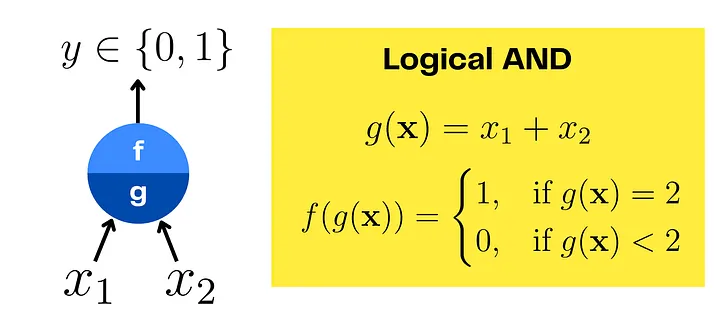
Снова попробуйте. Если оба входа равны 1, g = 2, следовательно f = 1. Иначе f = 0.
Общий МП-нейрон
В общем случае МП-нейрон может принимать любое количество входов и производить бинарный выход.
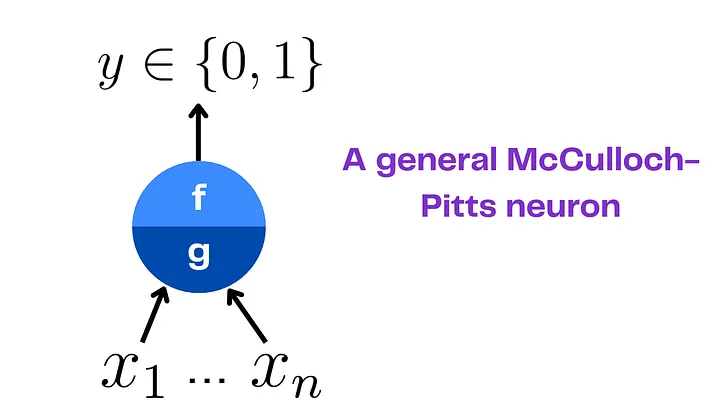
Функция g(x) – это взвешенная сумма: g(x) = Σ wi × xi, где wi представляет вес каждого входа.
Функция f(x) – это то, что мы называем функцией активации в современных нейронных сетях.
Тогда она была простой – ступенчатая функция.
Если g(x) > порога, то f(x) = 1. Иначе f(x) = 0.
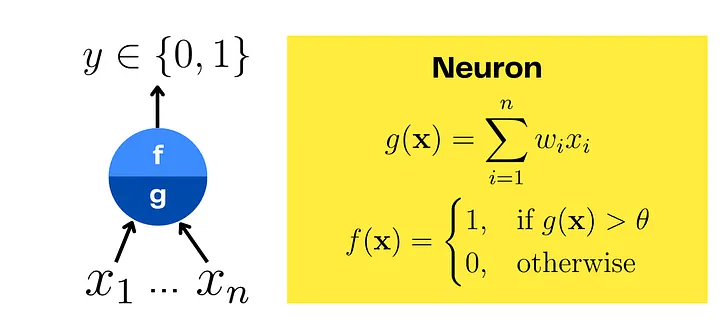
Аналогия с биологическим нейроном, который имеет множество входов и выдаёт импульс, если совокупная сумма входов превышает порог:
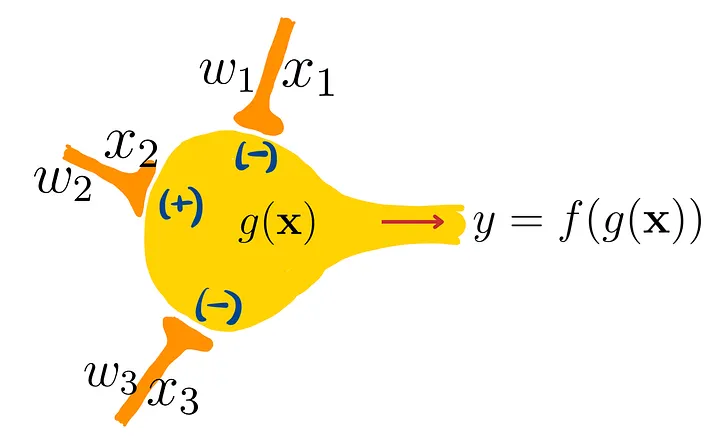
Вот и всё. Математическая абстракция биологического нейрона.
От математической абстракции 1943 года до облачных технологий
Путь от простого МП-нейрона Питтса и Маккалока до современных нейросетей занял 80 лет. Сегодня искусственный интеллект стал настолько доступным, что для работы с ним больше не нужны суперкомпьютеры или специальное оборудование.
Сервисы вроде BotHub предоставляют доступ к самым современным AI-моделям прямо из браузера.
Для доступа не требуется VPN, и можно использовать российскую карту.
По ссылке вы можете получить 100 000 бесплатных токенов для первых задач и приступить к работе прямо сейчас!
То, о чём мечтали Питтс и Маккалок – универсальная вычислительная модель мозга – сегодня доступно каждому. Не привязывайтесь к операционной системе. Привязывайтесь к инструментам, которые решают ваши задачи.
Трагический конец (и прекрасное наследие)
Питтс был перфекционистом.
Он хотел доказать, что мозг – это в точности булева схема, без исключений.
Но позже было обнаружено, что входные сигналы от глаза изначально обрабатываются в аналоговой форме, прежде чем быть преобразованными в цифровые сигналы в мозге. Его модель не была идеальной.
Он был разбит. Фактически, он был настолько разочарован, что сжёг собственную диссертацию.
В конце концов Питтс впал в депрессию и прожил последние годы в безвестности. Его история – напоминание о том, что перфекционизм иногда может стать врагом прогресса.
Вот в чём дело.
Совершенство ≠ Полезность
Нам не нужна идеальная модель, чтобы создать что-то полезное.
Даже сегодня, 80 лет спустя, никто не нашёл идеальной модели мозга, и слишком многое в биологии ещё предстоит понять. Представьте Питтса в 1943 году, предъявляющего к себе такие высокие стандарты.
И всё же работа, которую проделали Питтс и Маккалок, превратилась в эту огромную область ИИ, которая полностью меняет мир.
Иногда исследования идут не туда, куда вы ожидаете.
Вы можете искать одно, а обнаружить совсем другое. И это нормально.
Именно так совершаются прорывы.
Автор: cognitronn


