Marigold-DC

Привет! Сегодня я хочу рассказать про сеточку Marigold-DC решающую задачу Depth Completion.

Пользуясь случаем, оставляю ссылку на свой канал: notmagicneuralnetworks

Задача Depth Completion

Построение 3D мира стало необходимым с появлением автопилотов для построения карт и планирования маршрутов.

Лидар (Light Detection and Ranging) – это устройство, которое измеряет расстояние до объекта с помощью лазера. Устройство выстреливает лазерный луч и ловит его отражение, а по затраченному времени вычисляется расстояние до объекта. Количество таких лучей зависит от разрешения лидара. Их можно увидеть на роботах-пылесосах, беспилотном транспорте.

На видео показан 3D мир беспилотного автомобиля, который он видит с помощью лидара. 

Безусловное преимущество лидаров в том, что они обладают высокой точностью и скоростью, однако, лучи все-таки дискретные и 3D карта мира остается довольно разряженной.

Задачка Depth Completion пытается получить плотную 3D карту по лидарным точкам и изображениям с камер. В результате для каждого пикселя изображения должна быть известна глубина.

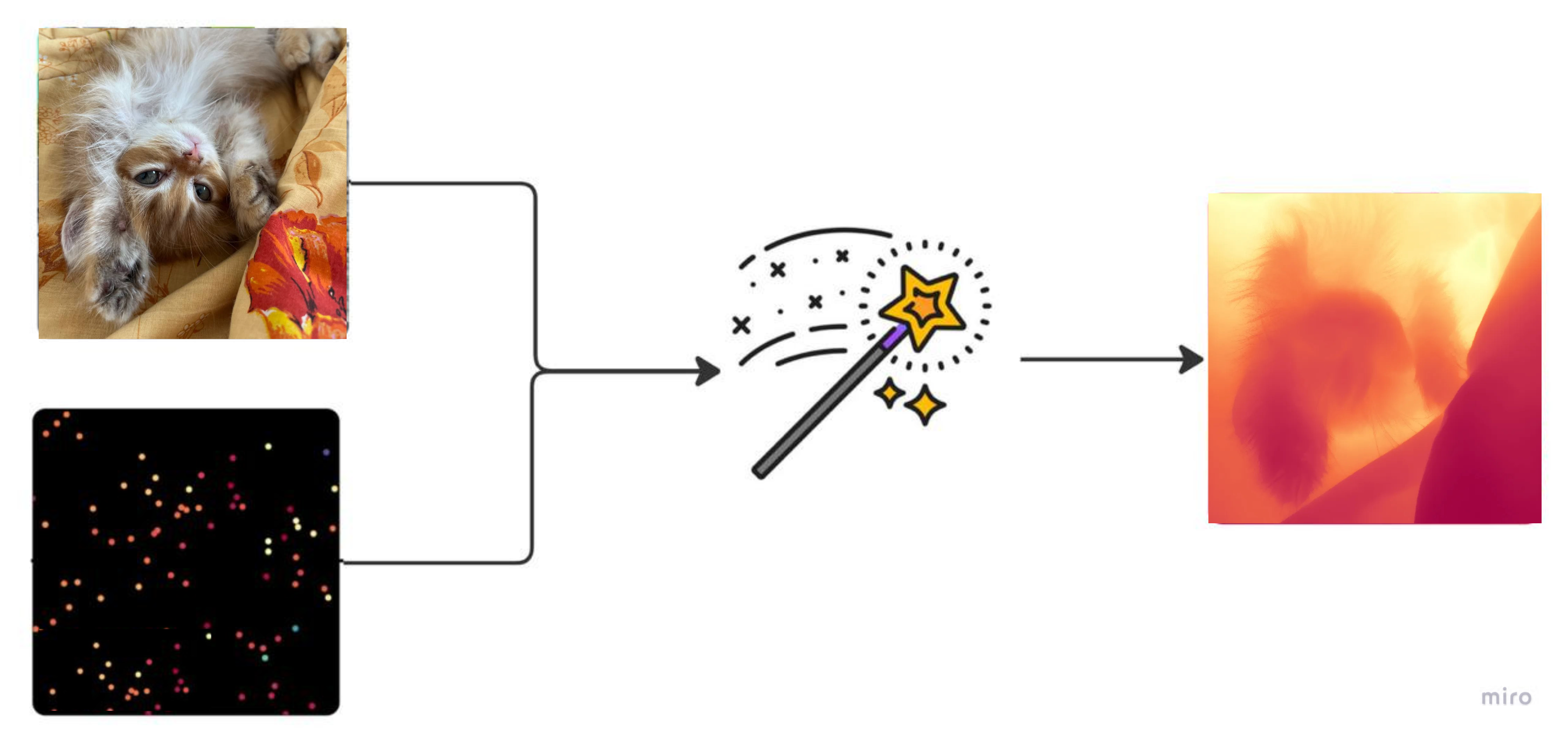
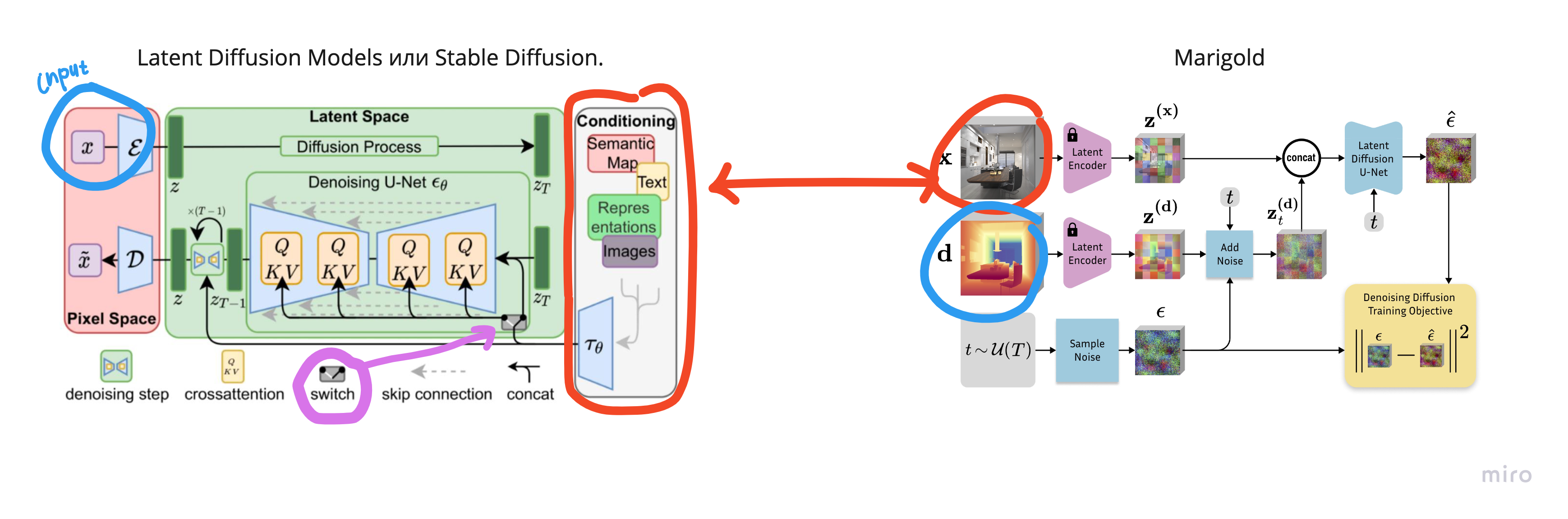
Marigold-DC – это одно из решений такой задачи. Marigold-DC является доработанной моделью Marigold, которая решает задачу Monodepth (построение карты глубины только по изображениям). В свою очередь, Marigold основана на Latent Diffusion Models (Stable Diffusion). А Stable Diffusion использует в своей архитектуре модель U-Net. 

В данной статье я попыталась разобраться в идеях перечисленных выше архитектур.

Marigold-DC -> Marigold -> Stable Diffusion -> U-Net

Marigold-DC

Мотивируют авторы свою работу (Marigold-DC) так, что есть различные сверточные сети, решающие задачу Depth Completion, однако, они плохо обобщают из-за недостатка обучающих данных. В то же время, с куда лучшим качеством, решается задача Monodepth, как раз за счет разнообразия датасетов и хороших знаниях о структуре мира. И вот, авторы решили объединить решение задачи Monodepth с Depth Completion. Кратко как они это сделали:

• Взяли генеративую модель Marigold, которая решает задачу Monodepth и возвращает относительную карту глубины на промежутке .

• По лидарным точкам обучили параметры scale и shift , с помощью которых можно перейти в метрическое пространство по формуле в промежуток .

• вычислили и вернули метрическую карту глубины.

При этом, при попытке подобрать параметры и с помощью метода наименьших квадратов дали значительно хуже результаты. Авторы списывают это на то что ground truth данные тоже не идеальны и недостаточно точные.

Саму же Marigold не обучают, а использую как есть, с ее обширными знаниями о мире. Оптимизируют параметры , и инициализированный шум в латентном пространстве карты глубины о котором будет чуть пониже.

Диффузионоки

Прежде чем разбираться в Marigold надо немного вспомнить как работают диффузионные модели. 

Пусть у нас есть изображение , на котором изображен . На каждой итерации будем зашумлять его каким-то , а саму функцию зашумления обозначим . В конце-концов вместо котика у нас должен остаться чистый шум. 

Обучим нейронную сеть, которая на каждой итерации, наоборот, будет пытаться очистить изображение от шума. Тогда, после такого обучения, когда мы возьмем какое-то и пропустим раз через , то получим нашего котика, но уже не совсем такого, какой он был изначально.

Пусть теперь модель находит шум в момент времени . Тогда процесс очищения будет состоять в том что мы будем вычитать этот шум из изображения, а в качеcтве функции потерь возьмем от реального шума и найденного шума в момент времени .

При этом у диффузионных моделей есть два больших недостатка:

1. Они требуют очень много данных для обучения.

2. Процесс генерации занимает очень много времени.

Эти проблемы пытались решить многие сетки, и одна из них – Latent Diffusion Models (Stable Diffusion).

Stable Diffusion

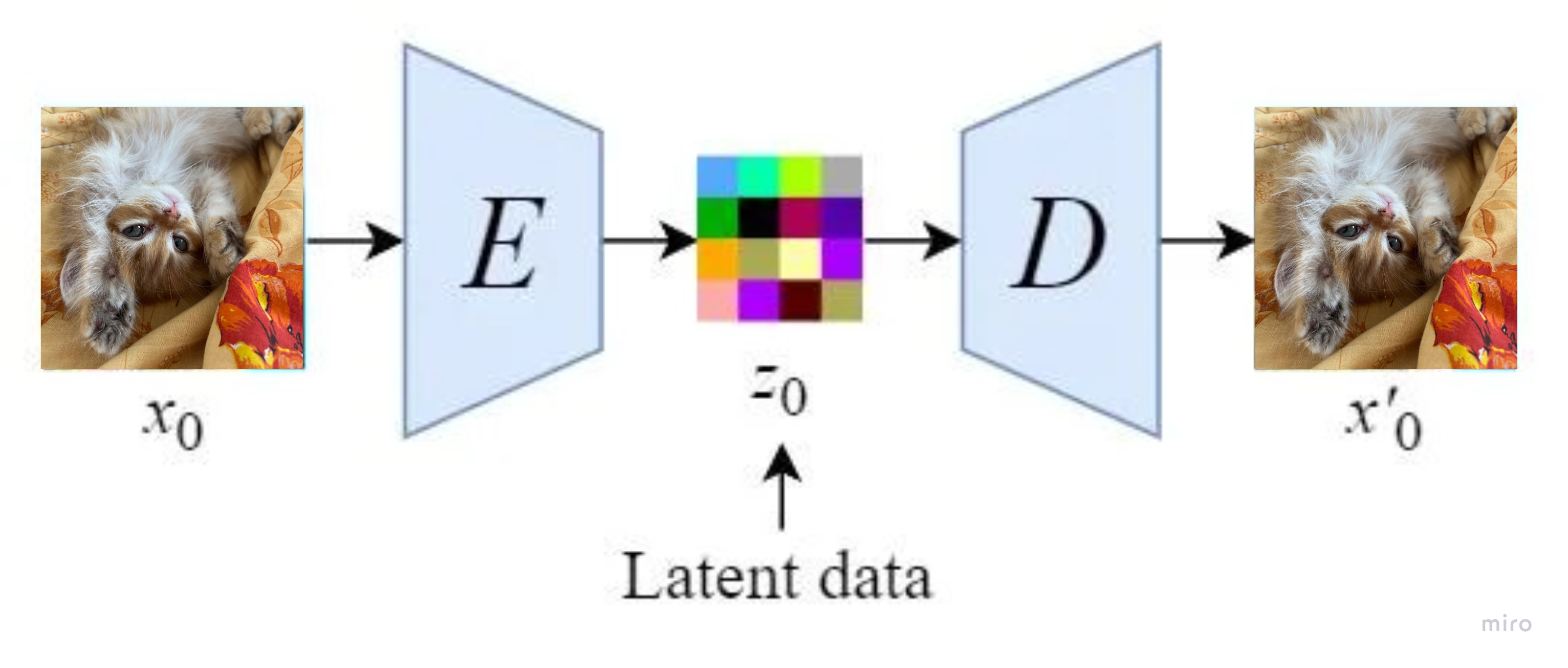
Идея Stable Diffusion заключается в том чтобы перейти от пиксельного пространства в латентное, которое гораздо меньших размерностей. Таким образом мы будем тратить гораздо меньше вычислительных ресурсов и процесс генерации будет происходить быстрее.

Вот как выглядит Latent Diffusion Models. 

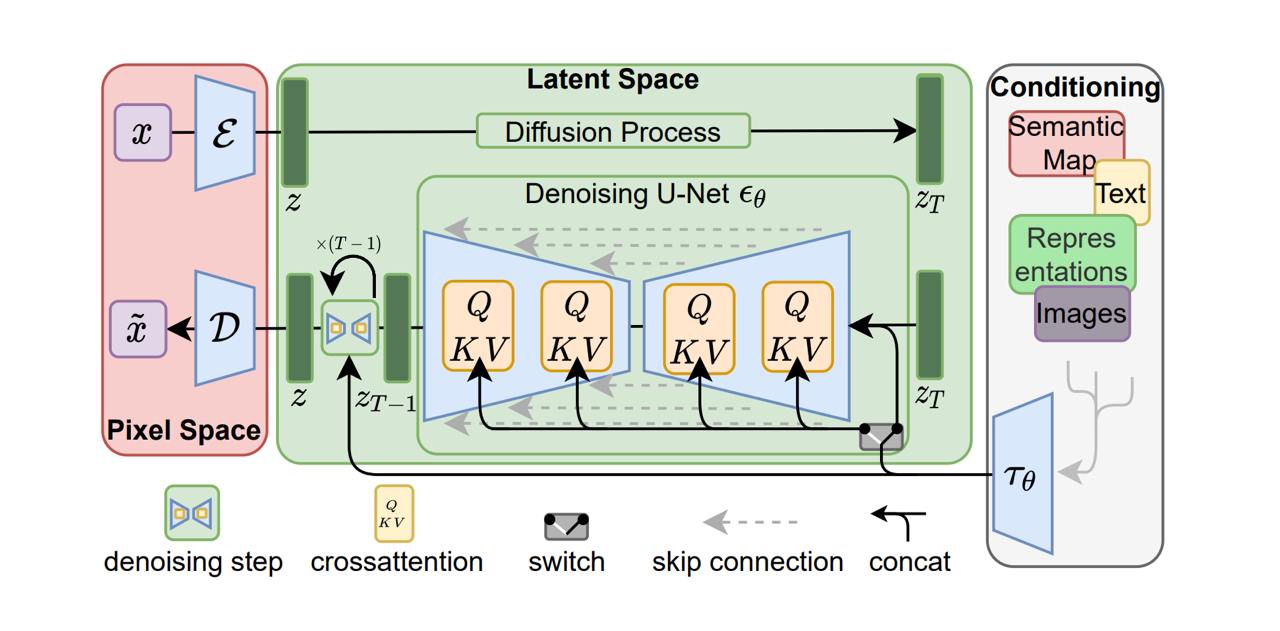
В верхней части входное изображение кодируется с помошью энкодера в латентное пространство (и становится ) и запускается процесс с зашумлением. Ниже, нейронная сеть U-Net, наоборот, пытается восстановить изображение из шума. После, декодируем с помощью и получаем обратно изображение. 

При обучении автокодирощика используется довольно сложная лосс-функция:

– (reconstruction) это между оригинальным изображением и изображением после применения энкодера и декодера – потеря данных автокодировщика. 

– (regularization) это -дивергенция между латентными данными и нормальным распределением (хотим чтобы они были похожи). Этот лосс выступает в форме регуляризации в латентном пространстве. 

– (adversarial manner following) потери генеративно-состязательной сети. Генератор стремится максимизировать вероятность того, что дискриминатор ошибается, а дискриминатор — минимизировать свою ошибку. В идеале, генератор научится создавать такие данные, которые трудно отличить от реальных.

Таким образом у Stable Diffusion два этапа обучения:

1. Обучение энкодера и декодера ( и ) для представления изображения в латентном пространстве и его восстановления.

2. Обучение диффузионной модели . На этом этапе энкодер и декодер уже должны быть обучены.

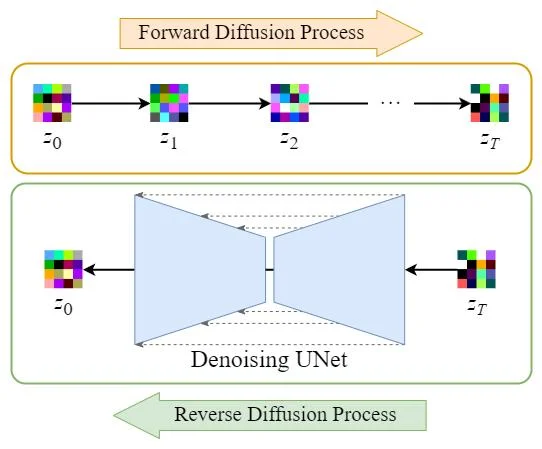
Denoising U-Net

U-Net свое название получила благодаря U-образной форме, где левая и правая часть являются энкодером и декодером соответственно. Появилась она еще в 2015 году в контексте задачи сегментации. 

Эта модель является общепринятой и, наверное, самой ходовой, в контексте диффузионных моделей. 

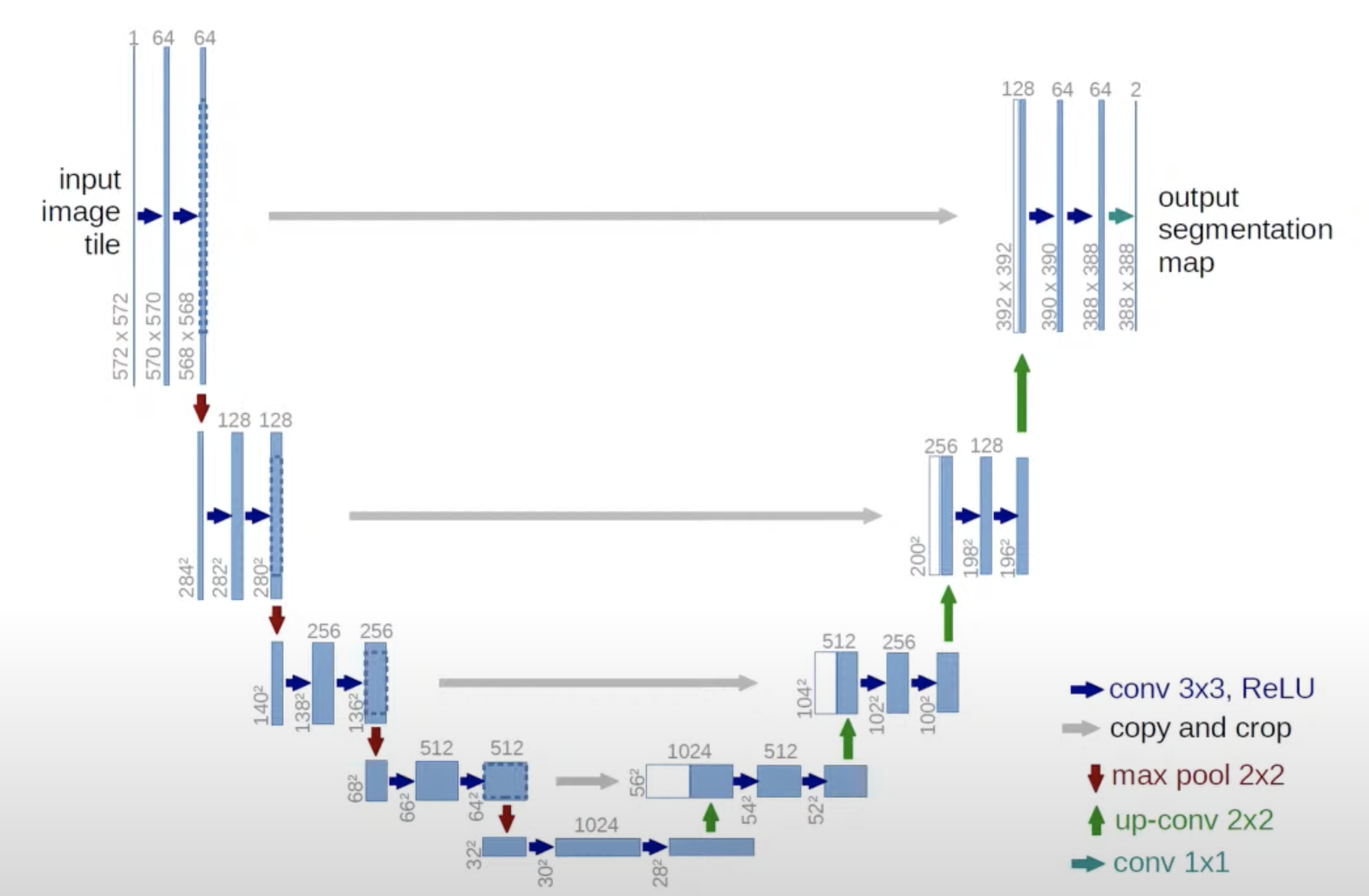
Состоит U-Net из конволюций, Res-блоков, конкатенаций и attention-блоков:

• Конволюции работают на разном разрешении: чем глубже слой, тем меньше изображение, но больше каналов.

• ResBlock-и почти не отличаются от ResNet: они содержат в себе конволюции, активации и нормализации, и это все конкатенируется с необработанной через этот блок частью фичей.

• Concatination соединяет фича-мапы которые не прогонялись в глубокие слои с тем что прогонялись, вдоль каналов. Это делается для лучшей сходимости и работы сети.

• Про attention в блоке сonditioning.

Conditioning

С помощью сonditioning мы говорим модели Stable Diffusion что именно нам нужно сгенерировать. И удобно, что на вход мы можно подавать что угодно: картинки, текст и тд.

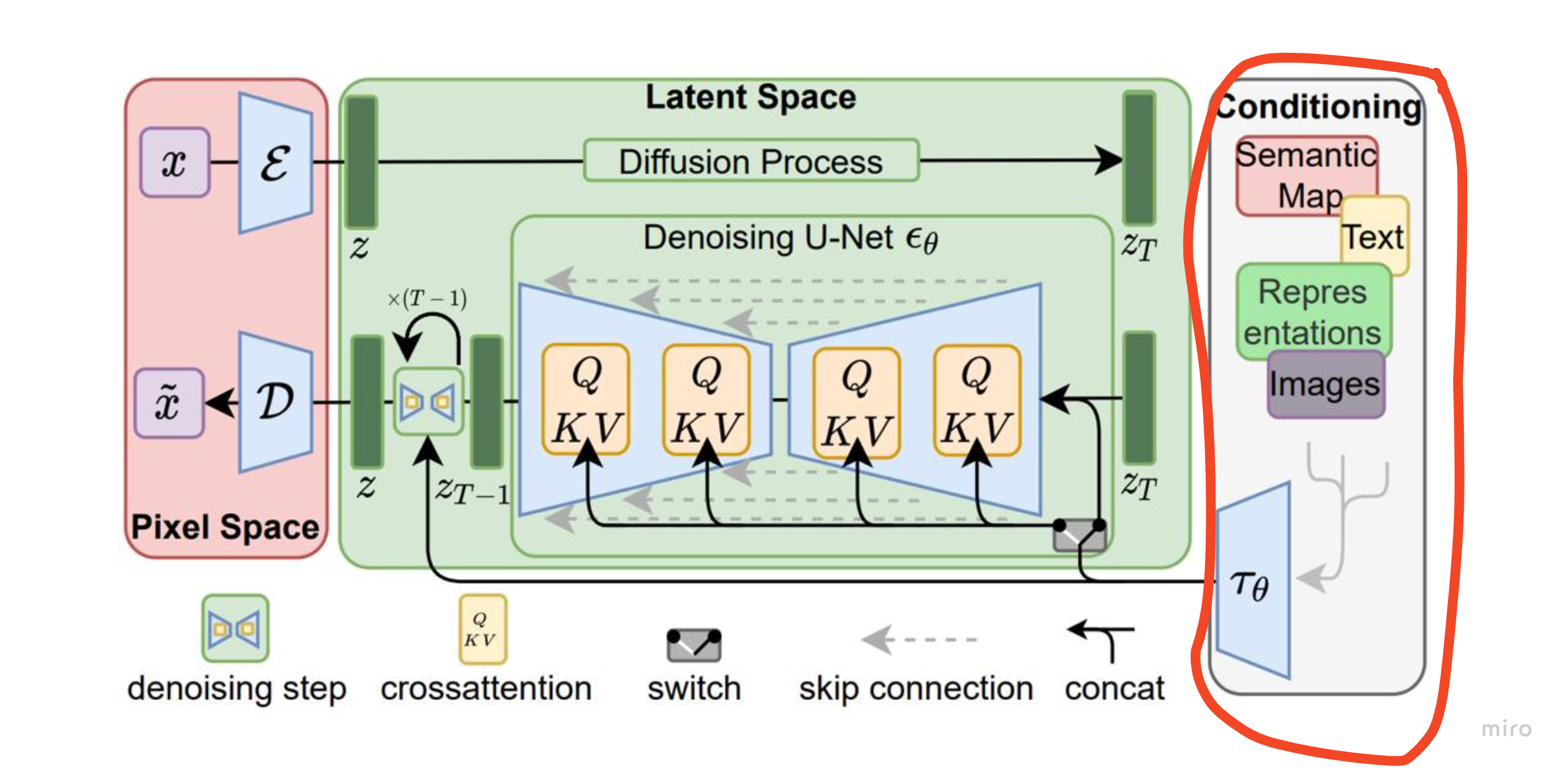
Главное закодировать эту информацию в латентное пространство. Например, можно генерировать изображения по текстовому описанию. В случае Marigold мы генерируем карту глубины по изображению. 

Добавлять при этом информацию можно разными способами с помощью switch: путем простого объединения с изображением, либо используя QKV-attention.

Для Marigold карта глубины выступала бы в качестве запроса Q(query), а изображение в виде набора пар ключ-значение K(key), V (value).

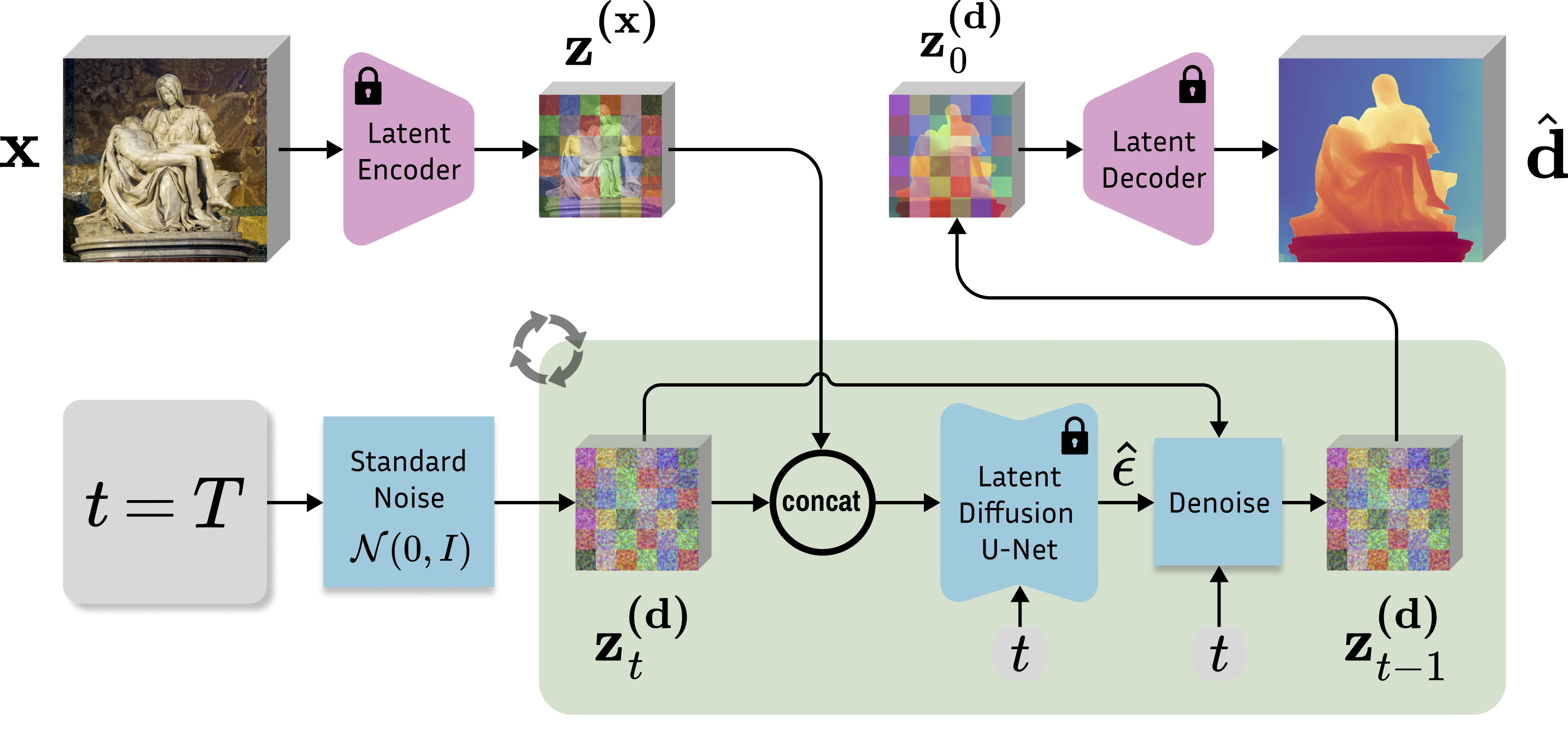
Marigold

Наконец, можно взглянуть на Marigold.

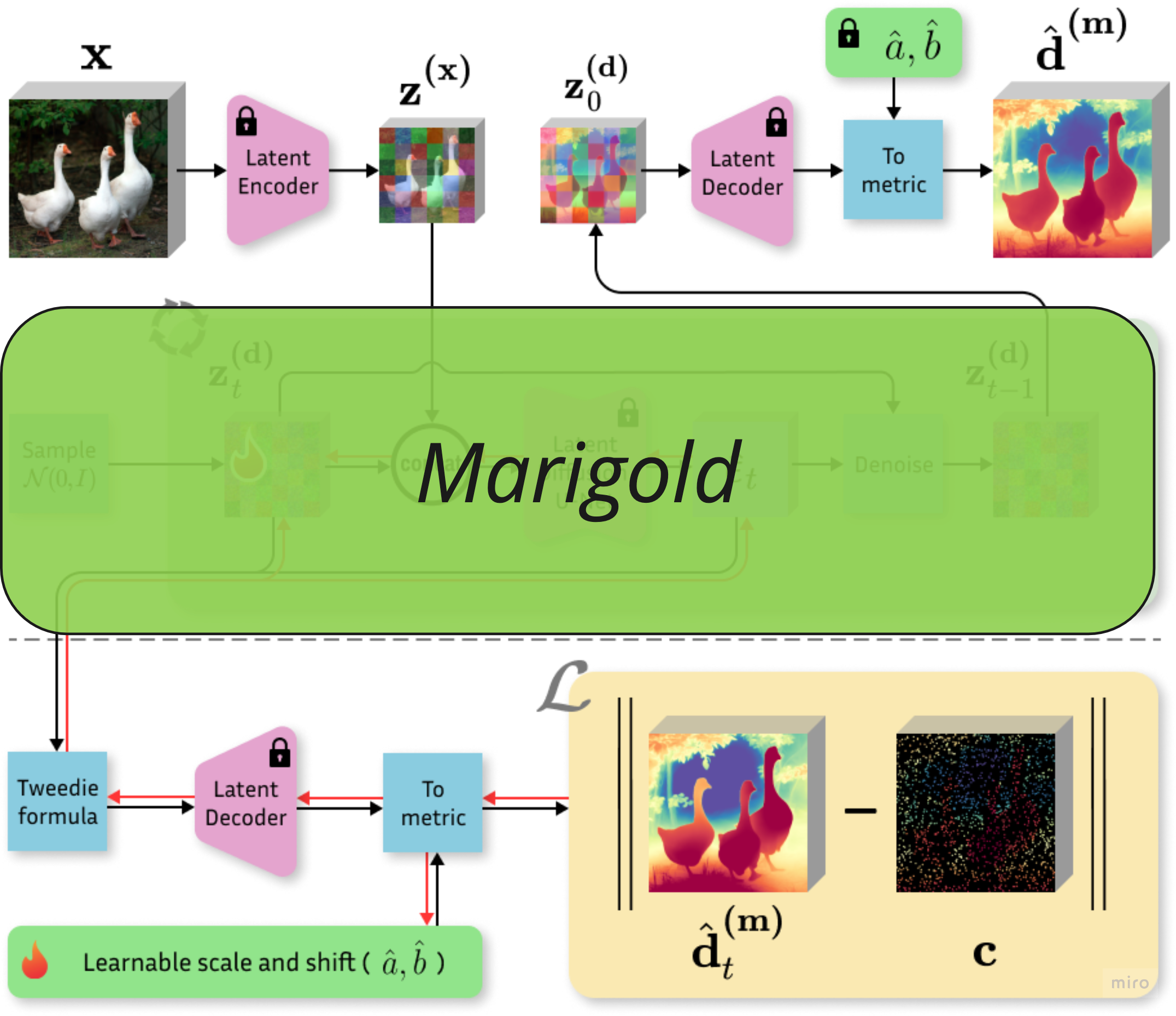
Во время обучения зашумляется и восстанавливается карта глубины, а изображение добавляется как сonditioning. Далее, мы видим всю ту же схему Stable Diffusion: перевод в латентное пространство с помощью энкодеров, добавление случайного шума и восстановление карты глубины.

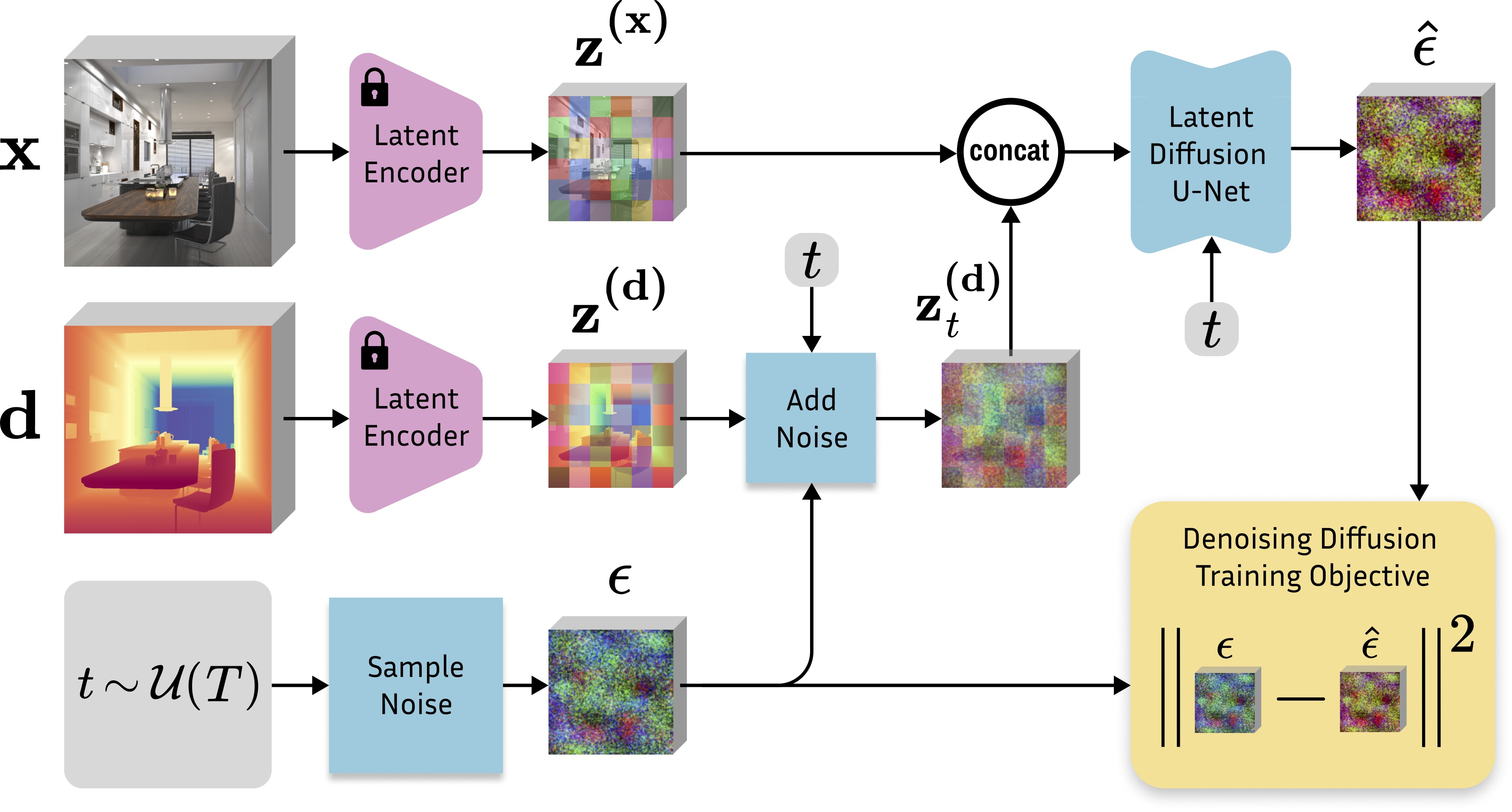
На инференсе же мы подаем только изображение и получаем карту глубины (потому что Marigold решает задачу Monodepth).

Собираем Marigold-DC

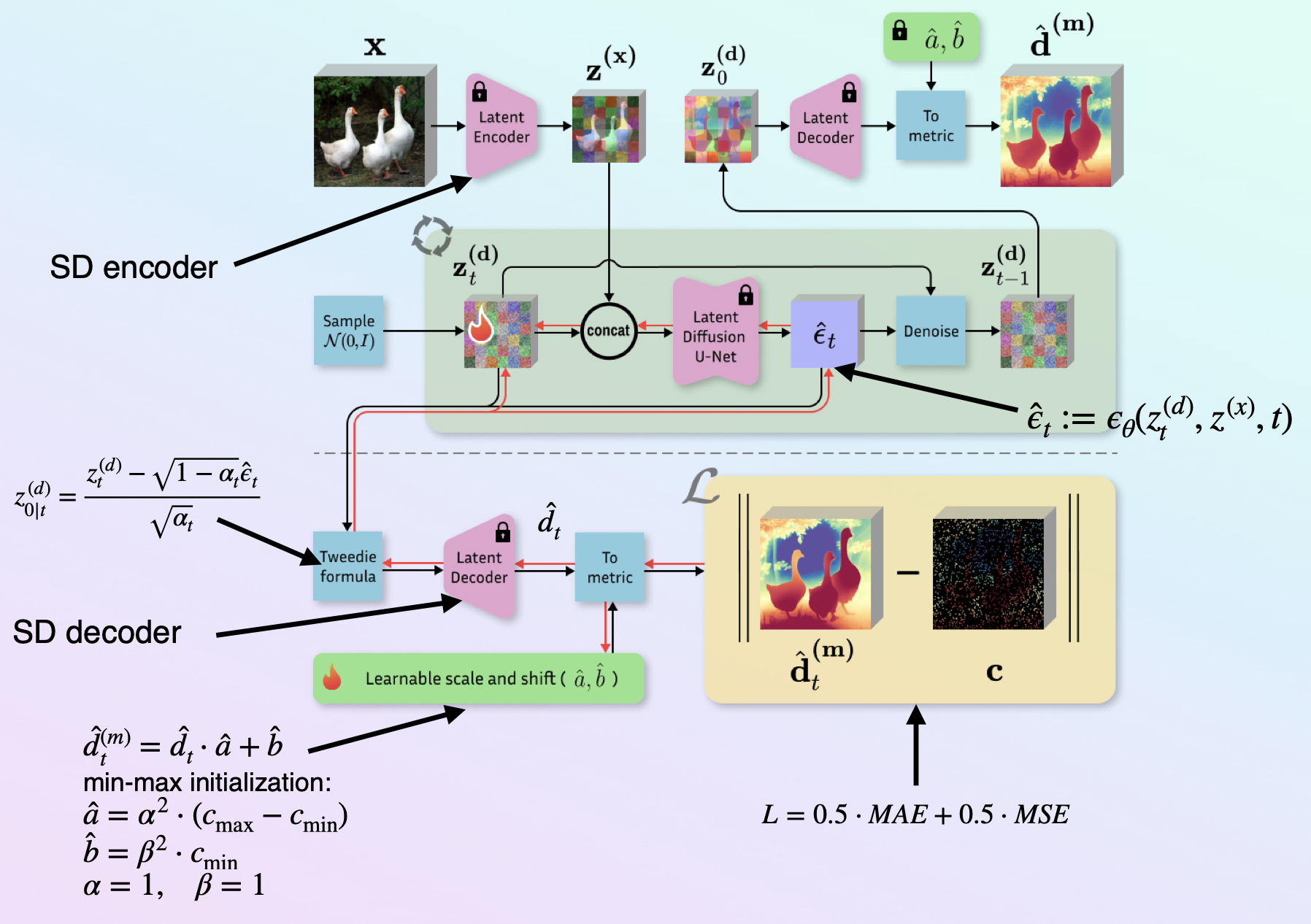
1. Переводим изображение в латентное пространство с помощью Stable Diffusion Encoder, получаем .

2. Инициализируем латентную глубину из нормального распределения .

3. Конкатенируем и .

4. Пропускаем через U-Net для получения оценки уровня шума .

5. Далее, вместо того чтобы делать sheduler step мы применяем формулу Твиди для получения “preview depth map” и пропускаем через Stable Diffusion Decoder. Получаем относительную карту глубины на промежутке [0, 1].

6. Пересчитываем карту глубины в метрическое пространство с помощью параметров(scale) and (shift). Если у нас первая итерация, то инициализируем следующим образом: и , где – лидарные точки.

7. Считаем Loss по полученной карте глубины и лидарным точкам (только там где лидарные точки определены) как равновзвешенные MAE и MSE.

8. Обновляем параметры , и . Сама Marigold при этом не обучается, используется как есть.

9. Делаем sheduler steps.

10. После всех sheduler steps делаем финальную denoising iteration и декодируем Stable Diffusion Decoder, получаем относительную карту глубины.

11. Применяем уже обученные (scale) and (shift).

12. Возвращаем предсказанную карту глубины в метрическом пространстве.

На практике

На практике Marigold-DC действительно показала хорошие результаты. Однако, поскольку сеть генеративная, она может додумывать какие-то атрибуты сцены.

Для настройки предоставлено два гиперпараметра:

• processing_resolution – разрешение, в котором обрабатывается изображение во время генерации (чем меньше processing_resolution, тем больше глюков).

• num_inference_steps – количество шагов, используемых в процессе диффузионной генерации изображения (чем больше шагов, тем больше какой-то ряби).

Оптимальные гиперпараметры указаны в статье Marigold-DC и, в целом, они совпали с теми что я считала для свой задачи (брала чуть меньше num_inference_steps).

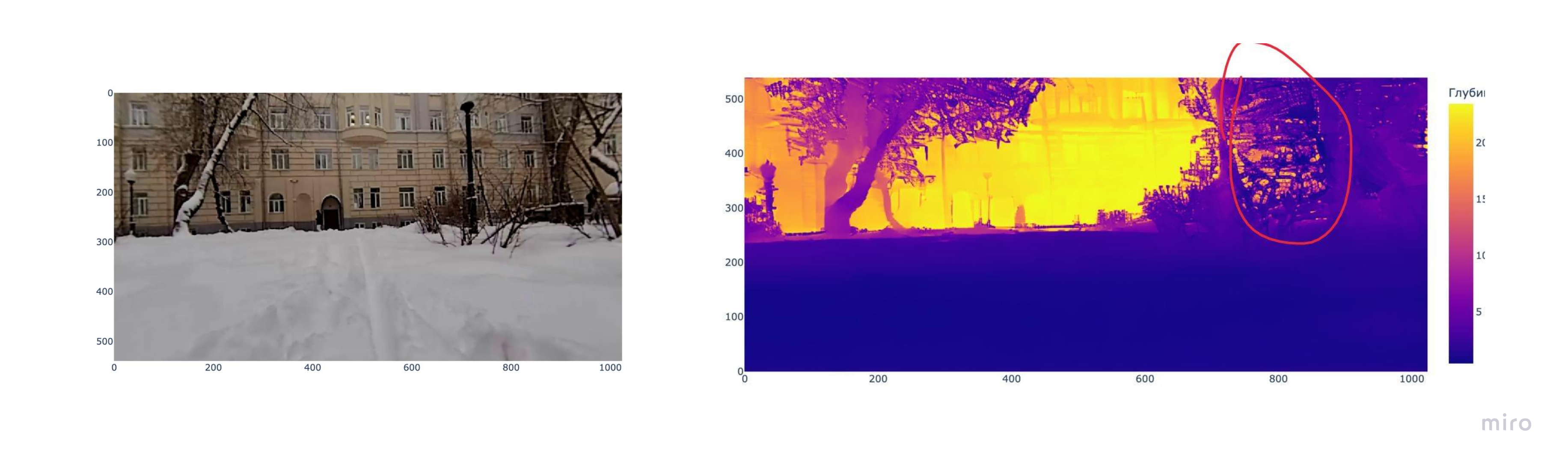
Проблема галлюцинаций часто возникает в областях, где нет лидарных точек. Например, если область очень далекая и лучи лидара оттуда не возвращаются.

И, скорее всего, из-за особенностей датасета, на котором обучалась Marigold, она часто предсказывает лишние датали на растениях или растения в пустых областях.

Полезные ссылки:

1. Marigold-DC: Zero-Shot Monocular Depth Completion with Guided Diffusion

2. Repurposing Diffusion-Based Image Generators for Monocular Depth Estimation

3. High-Resolution Image Synthesis with Latent Diffusion Models

4. U-Net: Convolutional Networks for Biomedical Image Segmentation

5. The KITTI Vision Benchmark Suite

6. CV Week Школы анализа данных

7. Генеративные модели, Хендбук

8. Stable Diffusion Clearly Explained!