RL (RLM): Разбираемся вместе

Всем привет! Недавно я познакомился с курсом по глубокому обучению с подкреплением от HuggingFace Deep Reinforcement Learning Course и захотел сделать выжимку самого интересного. Эта статья — своего рода шпаргалка по основам Reinforcement Learning (RL) и одному из ключевых алгоритмов — PPO, который лежит в основе тонкой настройки современных LLM (Large Language Models).

Вы наверняка слышали про такие модели, как o1 от OpenAI или QwQ от Alibaba. Их “рассуждающие” способности во многом — результат применения RL. Давайте разберемся, как обычный принцип обучения, известный по играм вроде AlphaGo, помогает языковым моделям стать умнее.

RLM – это

RLM (reasoning language model – дословно “рассуждающая языковая модель”) – это языковые модели, способные не только генерировать текст, но и выполнять логические, аналитические и причинно-следственные рассуждения для решения сложных задач.

Эти передовые системы в корне переопределили возможности ИИ по решению проблем, обеспечив тонкие рассуждения, улучшенное контекстное понимание и надежное принятие решений в широком спектре областей.

Рассмотрим 3-м столпа, на которых строится архитектура RLM:

1. Прогресс в LLM

2. RL алгоритмы, такие как AlphaZero

3. Ресурсы высокопроизводительных вычислений (eng. HPC)

На связи первых двух пунктов, я считаю, можно остановиться подробнее, так как для меня они были неочевидные.

Reinforcement Learning

Начну с самого банального – это определение Reinforcement Learning. Reinforcement Learning (RL), или обучение с подкреплением, — это способ машинного обучения, при котором агент учится принимать решения, взаимодействуя с окружающей средой. Проще говоря, это метод проб и ошибок с поощрением за успехи.

• Агент – обучающийся или принимающий решения субъект, который взаимодействует с окружающей средой. Чаще всего в роли агента выступает, например, персонаж игры, определенный робот (например, робот-рука), нейронная сеть и так далее.

• Окружающая среда – внешняя система или мир, внутри которого действует агент.

Процесс обучения представляет собой цикл (Возьмем шаг t =0):

1. Агент видит состояние () среды.

2. Совершает действие ().

3. Получает от среды вознаграждение () — численную оценку своего действия.

4. Переходит в новое состояние ().

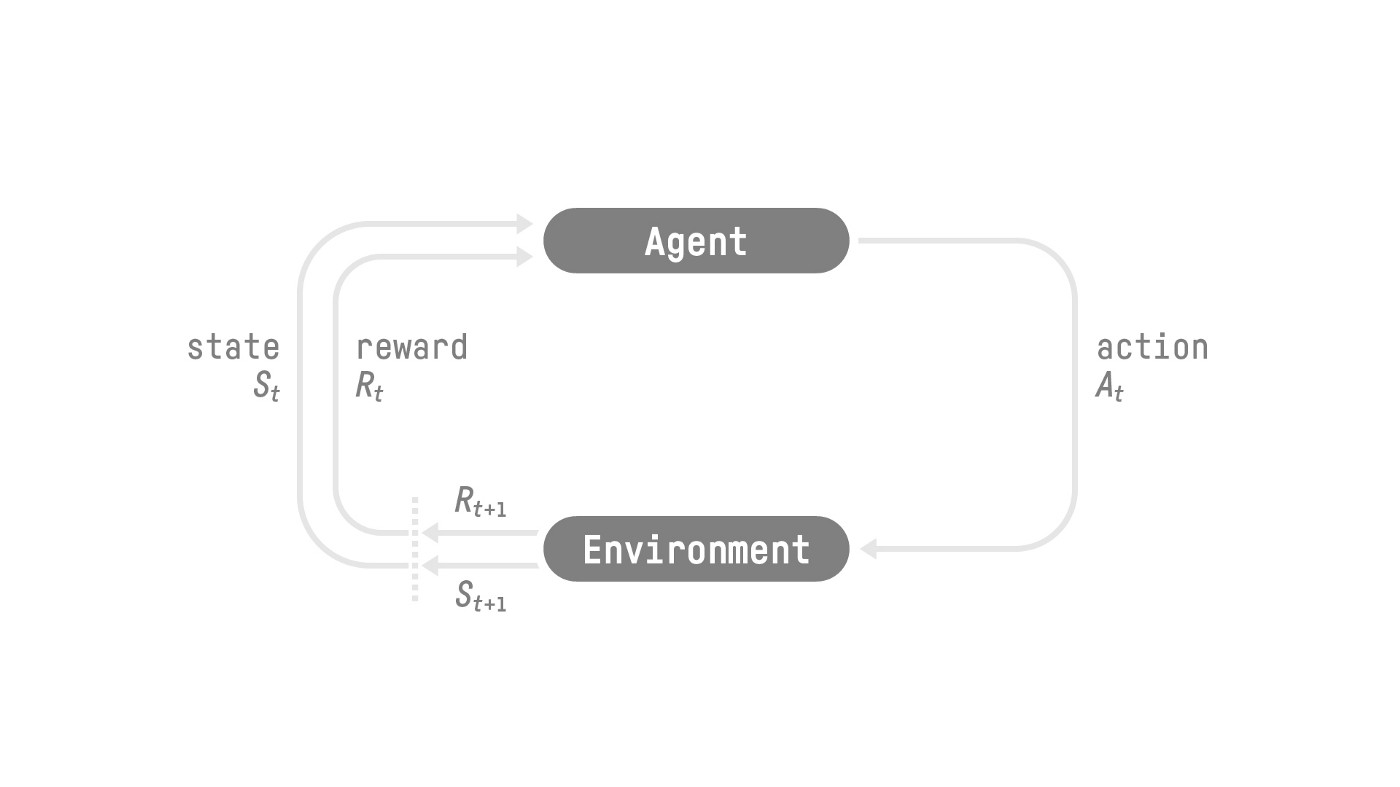
Именно такую схему описывает Марковский процесс принятия решений (MDP) — математическая основа для большинства алгоритмов RL (статья “Reasoning Language Models: A Blueprint” ).

Дадим каждой сущности последовательности определение:

Состояние (S) (или пространство состояний)- это информация, которую агент получает из окружающей среды.

Действия (A)(или пространство действий) – это набор всех возможных действий в среде.

Награды (R) – это по сути, наша обратная связь для агента на предпринятое действие. В плоскости LLM – в процессе рассуждения RLM может перейти из одного ответа в другой – как следствие получить положительное вознаграждение (если ответ от LLM корректный), так и отрицательное (если ответ некорректный).

Накопленное вознаграждение на каждом шаге t можно представить:

где – это последовательность чередующихся состояний и действий

Однако мы не можем просто так их складывать, потому что награды приходят раньше, более вероятны, поскольку они предсказуемы, чем долгосрочные будущие награды. Следовательно, вводим коэффициент дисконтирования такой, что:

• Значения варьируются в диапазоне от 0 до 1 (в большинстве случаев – между 0.95 и 0.99

• Чем больше гамма, тем меньше дисконт => агент заботится о долгосрочном вознаграждении

• Чем меньше гамма, тем больше дисконт => агент заботится больше о краткосрочном вознаграждении

Таким образом, приходим к окончательной формуле вознаграждения с коэффициентом дисконтирования:

Хорошо, мы определили формулу для вознаграждения, но появляется вопрос: как мы можем выбирать действия, которые максимизируют это ожидаемое совокупное вознаграждение агента, иными словами “Решить задачу MDP”? На этот вопрос есть ответ, но сперва дадим определения, которые помогут прийти к ответу:

Политика (policy)

Политика – это функция, присваивающая распределение вероятностей по пространству действий заданному состоянию.

Более формально:

где– набор распределений вероятностей в пространстве действий A (ничего не напоминает? – посматриваю в сторону нейронных сетей и принцип действия LLM)

Таким образом, наша цель для решения задачи MDP – это найти оптимальную политику , которая максимизирует ожидаемую доходность (return), когда агент действует согласно ей. Находим оптимальную политику посредством обучения.

Методы обучения агента по поиску оптимальной политики

Мы все ближе к пониманию как решить задачу MDP, останавливают нас только подходы к обучению. Итак, выделяют 2 вида:

1. Обучение напрямую – заставляем агента понимать, какие действия следует предпринять с учетом текущего состояния (Policy-Based Methods).

2. Косвенно – учим агента узнавать, какое состояние будет более ценно, а затем предпринимать действия, которые ведут к более ценным действиям: методы, основанные на ценностях (Value-Based Methods).

Давайте кратко рассмотрим 2 этих подхода:

Policy-based методы

Агент учит политику () — прямую инструкцию “что делать в состоянии S”. Политика говорит не “делай Х”, а “с вероятностью 70% сделай Х, с вероятностью 30% — Y”. Именно так работают современные LLM, доработанные с помощью RL. Если кратко, то:

• Напрямую обучаем функцию политики выбирать действие, учитывая состояние (или распределение вероятностей по действиям в этом состоянии).

• Нет функции значения (value function)

• Есть 2 типа политик:

  • Детерминированная (политики в заданном состоянии будет возвращать одно и то же действие)

  • Стохастический (выводит распределение вероятностей по действиям) –

Value-Based методы

Агент учит функцию ценности (Q или V), а потом просто выбирает действие, которое ведет в самое “ценное” следующее состояние.

• В данном подходе обучаем функцию значения (Value function), которая сопоставляет состояние (или action-state пары) с ожидаемым значением нахождения в этом состоянии.

• Значение состояния (value state) – это ожидаемая дисконтная доходность (return), которую агент может получить, если начнет из определенного состояния и продолжит действовать в соответствии с политикой. Формально данное высказывание можно записать как:

где – это ожидаемая дисконтная доходность (return)

Разница между 2-мя подходами в следующем (согласно HuggingFace):

• При обучении Policy-Based метода оптимальная политика (обозначаемая ) находится путем непосредственного обучения политики.

• При обучении на основе ценностей  нахождение оптимальной функции ценности (обозначаемой Q* или V*, мы рассмотрим разницу ниже) приводит к появлению оптимальной политики.

• Policy-Based методы более естественны для задач, где действия непрерывны (как генерация текста), а Value-Based часто применяются в играх с дискретным набором ходов

Так как замечаем, что возникают “какие-то” функции Q и V – приходим к выводу, что у нас есть 2 типа value-based functions:

• The state-value function

  • Для каждого состояния функция «состояние-значение» выводит ожидаемый доход, если агент начинает с этого состояния , а затем следует политике вечно

• The action-value function

  • В функции «действие-значение» для каждой пары «состояние-действие» функция «действие-значение»  выводит ожидаемый результат,  если агент начинает в этом состоянии, выполняет это действие, а затем следует политике вечно

где (насколько я могу судить) авторы привели сокращенный вариант формулы и использовали просто замену:

Насколько можно заметить, в данных уравнениях мы повторяем вычисление значений различных состояний, что может быть вычислительно затратно, если вам нужно делать это для каждого значения состояния (state value) или значения состояния-действия (state-action value).

Вместо расчета ожидаемой доходности для каждого состояния или каждой пары состояние-действие  мы можем использовать уравнение Беллмана.

Таким образом, приходим к упрощенным вариантам этих формул:

• The state-value function

• Action-value function

С этой частью разобрались… можно выдохнуть… чуть-чуть… =)

Стратегии обучения

Монте-Карло

Монте-Карло использует целый эпизод перед обучением. То есть сначала ожидание эпизода, вычисление и далее обновление . Более формально:

Temporal Difference learning (TDL)

TDL использует только одно взаимодействие (то есть 1 шаг) для формирования TD цели и обновления , используя и (так как не проходим эпизод полностью и не знаем ).

(На курсе приведен классный пример с мышкой, иллюстрирующий эту формулу)

PPO

Наконец-то добрались до самой интересной части (если вы не устали от формул и не ушли с этой статейки), ради которой я и затевал эту статью – разобрать до полного понимания PPO – Proximal Policy Optimization — это алгоритм градиента политики, который позволяет стабильно обучать policy-based агентов, и именно он используется для тонкой настройки LLM (например, в RLHF).

Хотелки, которые лежали в основе PPO – это повысить стабильность обучения политики.

Идея заключалась в том, что выполняя шаг градиентного подъема по этой функции (эквивалентно выполнению градиентного спуска отрицательной функции), мы подталкиваем нашего агента к совершению действия, которые приведут к более высокому вознаграждению и избежанию вредных действий.

В чем была проблема?

Представьте, что вы учитесь ходить по канату. Если делать слишком маленькие шаги, вы никуда не дойдете. Если сделать слишком резкий и большой шаг — вы упадете. Так же и в RL:

1. Слишком маленький шаг – процесс обучения медленный

2. Слишком большой шаг – слишком мало вариаций в обучении

Идея PPO: “Доверяй, но проверяй”

Таким образом, приходим к идеи PPO – ограничить обновление политики с помощью новой целевой функции (Clipped), которая будет ограничивать изменения политики в небольшом диапазоне с помощью “клипа”, иначе она не позволит новой политике () слишком сильно отклоняться от старой ().

Таким образом, получим формулу для PPO с Clipped Surrogate Objective:

•  (Probability Ratio): Отношение вероятностей действия по новой и старой политике. .

  • : Действие стало более вероятным.

  • : Действие стало менее вероятным.

• (Advantage): Насколько действие в данном состоянии лучше, чем “среднее” действие по текущей политике. . Положительное преимущество означает, что действие стоит поощрять, отрицательное — что его следует избегать.

• Clipping (Обрезка): Самая важная часть PPO. Мы “обрезаем” значение  не позволяя ему выходить за пределы диапазона 

•  (Clip Range): Гиперпараметр, обычно равный 0.2. Он определяет диапазон  (т.е. ), за пределами которого функция “обрезается”

Отлично! Мы рассмотрели ключевые механизмы PPO и теперь стоит задуматься – где нам применять эти знания в плоскости LLM? Далеко ходить не надо – одно из самых значимых применений PPO сегодня — обучение с подкреплением на основе человеческих предпочтений (Reinforcement Learning from Human Feedback, RLHF) для согласования LLM, таких как ChatGPT и Llama 2.

Процесс RLHF состоит из нескольких этапов, и PPO является ядром этого процесса:

• Шаг 1: Начальная тонкая настройка с учителем (SFT)

  • Модель обучается на наборе высококачественных данных “вопрос-ответ”, чтобы научиться следовать инструкциям

• Шаг 2: Обучение Модели Вознаграждения (Reward Model, RM)

  • Создается отдельная модель, которая учится предсказывать, какой из двух ответов на один вопрос человек оценит выше. Эта модель заменяет человека в цикле обучения и выдает скалярную оценку (reward) для любого сгенерированного текста

• Шаг 3: Fine-Tuning с помощью PPO

  • На этом этапе SFT-модель становится агентом, политику () которого нужно оптимизировать.

Архитектура обучения в этот момент включает несколько моделей:

1. Актор (Actor): Текущая политика (LLM), которую мы обновляем с помощью PPO.

2. Критик (Critic): Сеть, которая оценивает value-function (), чтобы снизить дисперсию Advantage-функции. (в курсе HuggingaFace есть классный раздел про Actor-Critic)

3. Модель вознаграждения (Reward Model): Выдает основное вознаграждение.

4. Референсная модель (Reference Model): Замороженная копия исходной SFT-модели, используемая для расчета KL-штрафа

И в конце – давайте порисуем!

Для понимания как работает PPO – создадим пару простых примеров на python и визуализируем:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

def plot_ppo_clipping_mechanism():
    """График 1: Механизм клиппинга"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))

    # Левый график - функция потерь PPO
    r_theta = np.linspace(0.1, 3, 100)
    advantage = 1.0  # Положительное преимущество
    epsilon = 0.2

    # PPO clipped objective
    clip_min = 1 - epsilon
    clip_max = 1 + epsilon

    unclipped = r_theta * advantage
    clipped = np.clip(r_theta, clip_min, clip_max) * advantage
    ppo_loss = np.minimum(unclipped, clipped)

    ax1.plot(r_theta, unclipped, 'r--', alpha=0.7, label='Без клиппинга')
    ax1.plot(r_theta, clipped, 'g--', alpha=0.7, label='Clipped')
    ax1.plot(r_theta, ppo_loss, 'b-', linewidth=2, label='PPO Loss')
    ax1.axvline(x=1, color='k', linestyle=':', alpha=0.5)
    ax1.axvspan(clip_min, clip_max, alpha=0.2, color='green', label='Область клиппинга')
    ax1.set_xlabel('r(θ) = π_new/π_old')
    ax1.set_ylabel('Loss')
    ax1.set_title('Функция потерь PPO с клиппингом')
    ax1.legend()
    ax1.grid(True, alpha=0.3)

    # Правый график - сравнение стабильности
    episodes = np.arange(1000)

    # Имитация обучения разных алгоритмов
    np.random.seed(42)

    # PPO - плавный рост
    ppo_reward = np.cumsum(np.random.normal(0.1, 0.3, 1000))
    ppo_reward = np.maximum(ppo_reward, 0)

    # TRPO - возможны резкие падения
    trpo_reward = np.cumsum(np.random.normal(0.15, 0.8, 1000))
    trpo_reward = np.maximum(trpo_reward, 0)

    ax2.plot(episodes, ppo_reward, 'b-', label='PPO', linewidth=2)
    ax2.plot(episodes, trpo_reward, 'r-', label='TRPO', alpha=0.7)
    ax2.set_xlabel('Эпизоды')
    ax2.set_ylabel('Награда')
    ax2.set_title('Сравнение стабильности обучения')
    ax2.legend()
    ax2.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.show()

def plot_kl_control_in_rlhf():
    """График 4: KL-контроль в RLHF"""
    iterations = np.arange(200)

    # Имитация различных стратегий контроля KL
    np.random.seed(42)

    # Без KL-штрафа
    no_kl = np.cumsum(np.random.normal(0.2, 0.3, 200))

    # С фиксированным KL-штрафом
    with_kl = 2 + np.sin(iterations * 0.1) + np.random.normal(0, 0.1, 200)

    # Адаптивный KL
    adaptive_kl = 1.5 + 0.5 * np.sin(iterations * 0.05) + np.random.normal(0, 0.05, 200)

    plt.figure(figsize=(12, 6))
    plt.plot(iterations, no_kl, 'r-', label='Без KL-штрафа', linewidth=2)
    plt.plot(iterations, with_kl, 'g-', label='С KL-штрафом', linewidth=2)
    plt.plot(iterations, adaptive_kl, 'b-', label='Адаптивный PPO', linewidth=2)

    # Целевой диапазон
    plt.axhspan(1.0, 2.0, alpha=0.2, color='green', label='Целевой диапазон KL')

    plt.xlabel('Итерации PPO')
    plt.ylabel('KL-дивергенция')
    plt.title('Контроль KL-дивергенции в RLHF для LLM')
    plt.legend()
    plt.grid(True, alpha=0.3)
    plt.show()

# Запуск визуализаций
plot_ppo_clipping_mechanism()
plot_kl_control_in_rlhf()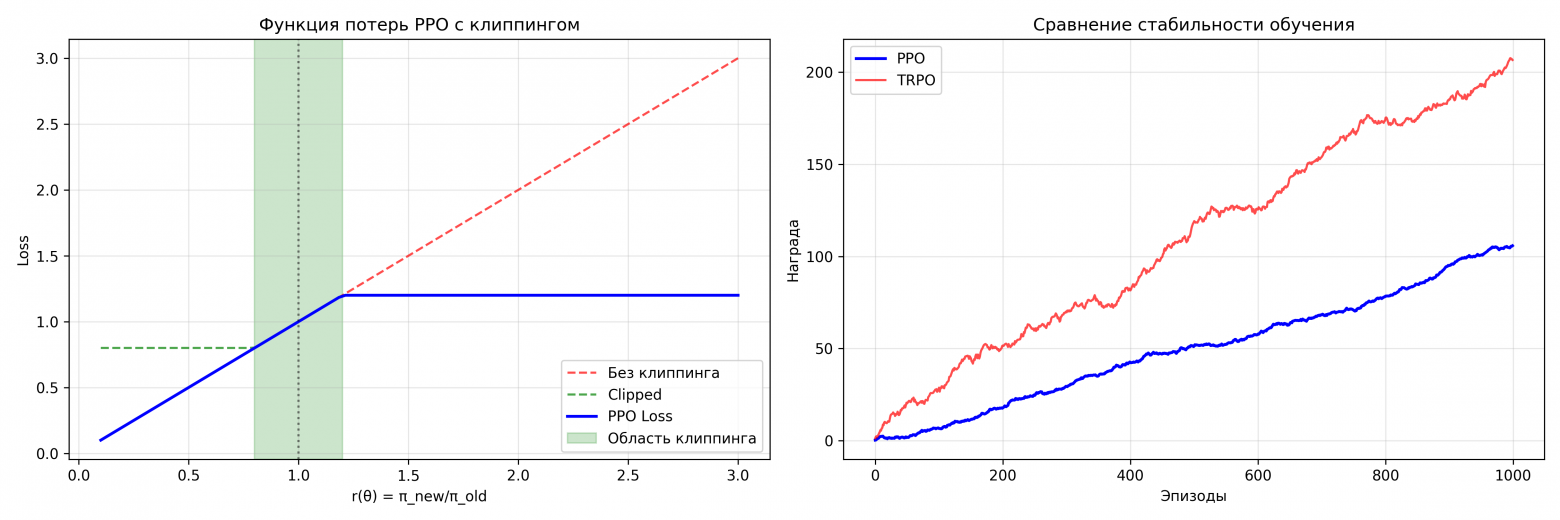

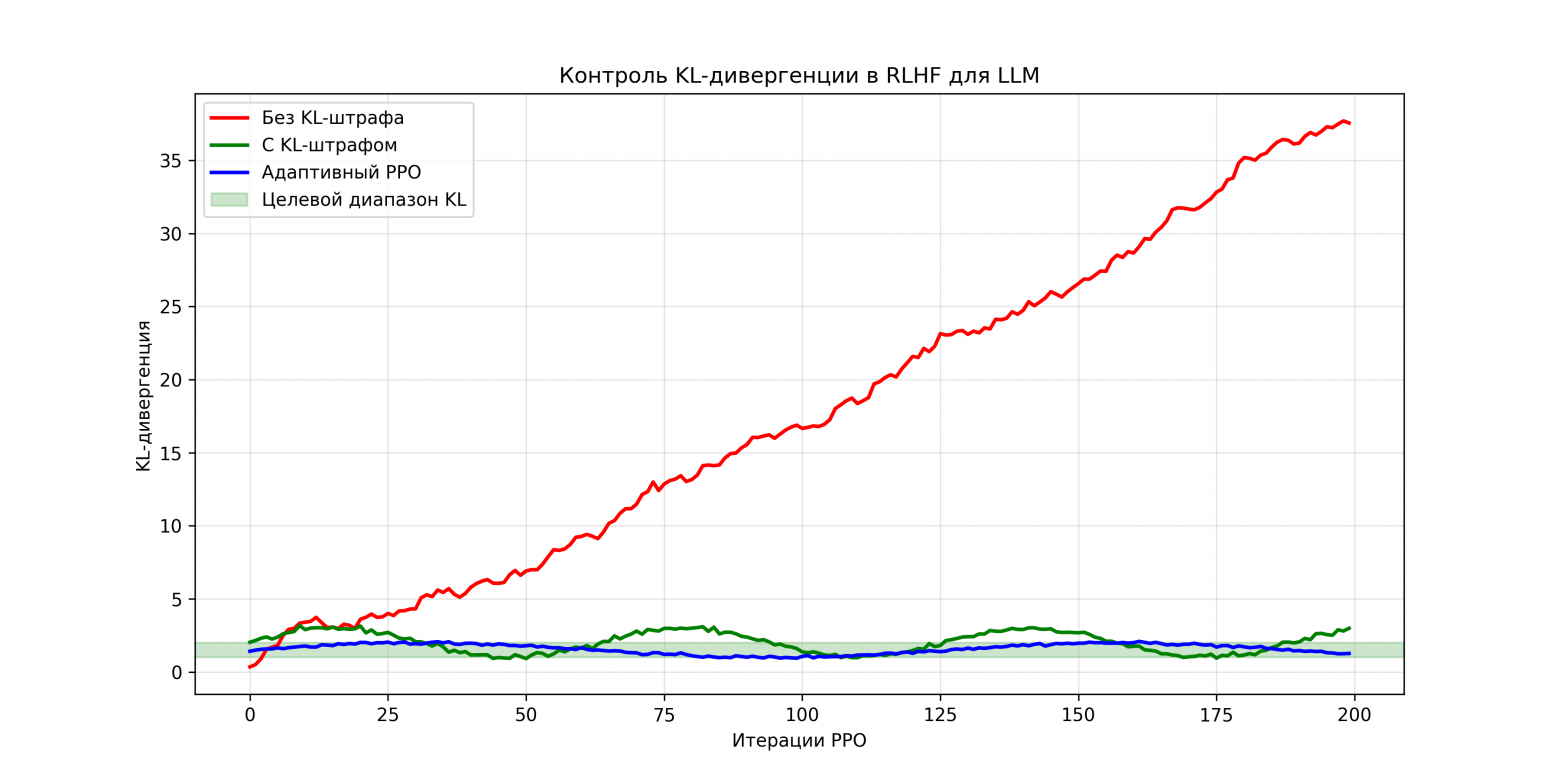
Главные выводы из графиков:

1. График 1: PPO создает “песочницу” для обновлений политики – внутри зеленой зоны алгоритм свободно экспериментирует, но не может выйти за безопасные границы.

2. График 2: По сравнению с TRPO (предшественник PPO), PPO показывает более плавную и предсказуемую динамику обучения без резких катастрофических падений.

3. График 3:

   1. По мере стабилизации политики клиппинг применяется реже.

   2. В RLHF критически важно контролировать KL-дивергенцию, иначе модель может “убежать” в странные области пространства политик.

Именно благодаря Probability Ratio и механизму клиппинга PPO стал таким эффективным для RLHF — он находит баланс между обучением новому поведению и сохранением существующих capabilities модели

Обязательно оставляйте комментарии!

Будут неточности – пишите, если понравилась статья и она Вам помогла понять аспекты RL/RLHF – тоже пишите!

Всех обнял приподнял!!!