Представьте себе нейрон в человеческом мозге. Или ветвь старого дерева. Или тончайшую сеть капилляров под кожей. На первый взгляд — совершенно разные вещи, рожденные разными законами и эпохами эволюции. Но современная физика все чаще показывает: природа любит повторять удачные решения. Иногда — с почти математической точностью.
Недавно ученые сделали шаг, который еще пару десятилетий назад показался бы эксцентричным: они взяли инструменты теории струн — одной из самых абстрактных областей теоретической физики — и применили их к… биологии. Результат оказался неожиданно наглядным.
Более ста лет господствовала простая и интуитивная гипотеза: живые системы формируют свои сети так, чтобы минимизировать длину. Меньше длина — меньше материала, меньше энергии, выше эффективность. В математике такие сети описывались как тонкие линии или провода, соединяющие точки кратчайшим путем. Эта идея выглядела красиво, но при сравнении с реальными биологическими структурами она регулярно давала сбои: тройные и четверные разветвления, тонкие боковые отростки, ветви, растущие почти под прямым углом.Согласитесь, с точки зрения минимизации длины — странно и невыгодно. С точки зрения живых систем — повсеместно.
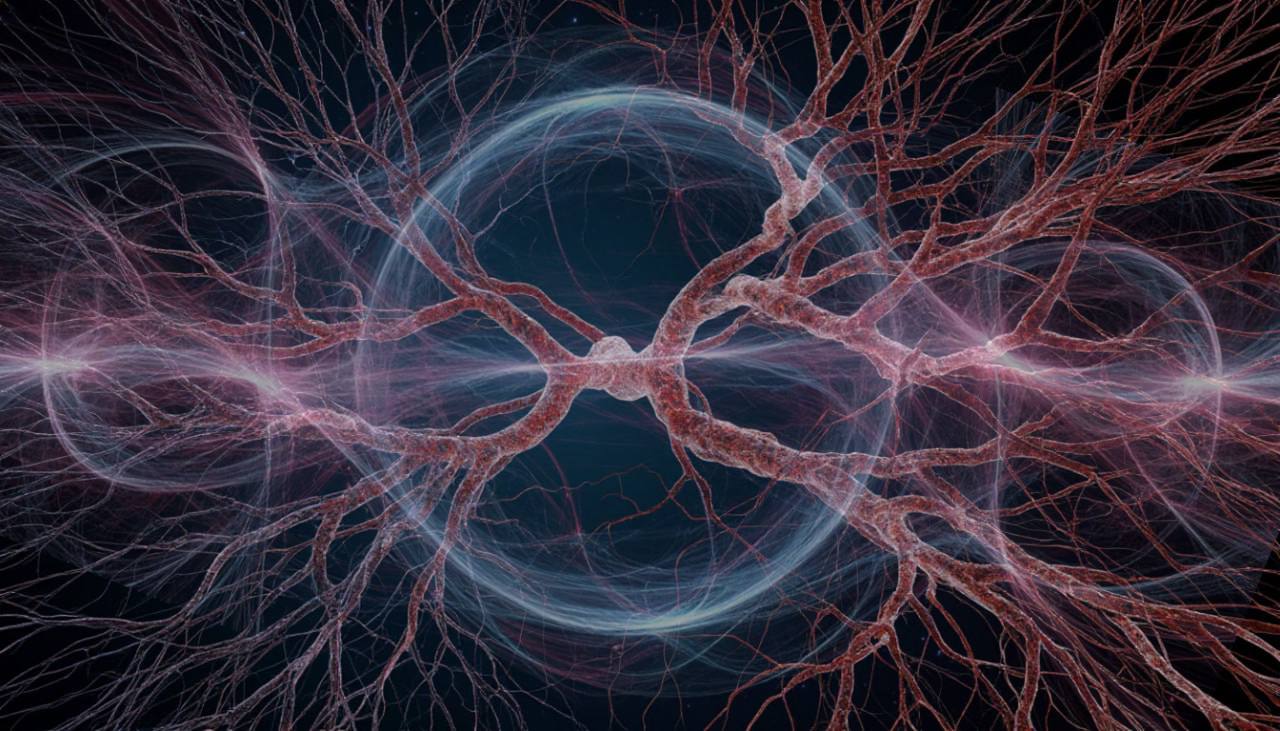
Тогда физики из Политехнического института Ренсселера обратили внимание на принципиальный (хоть и очень очевидный) момент: биологические сети — это не одномерные линии, а непрерывные трехмерные объекты. У них есть толщина, объем и — главное — поверхность. Именно здесь неожиданно пригодился математический аппарат теории струн.
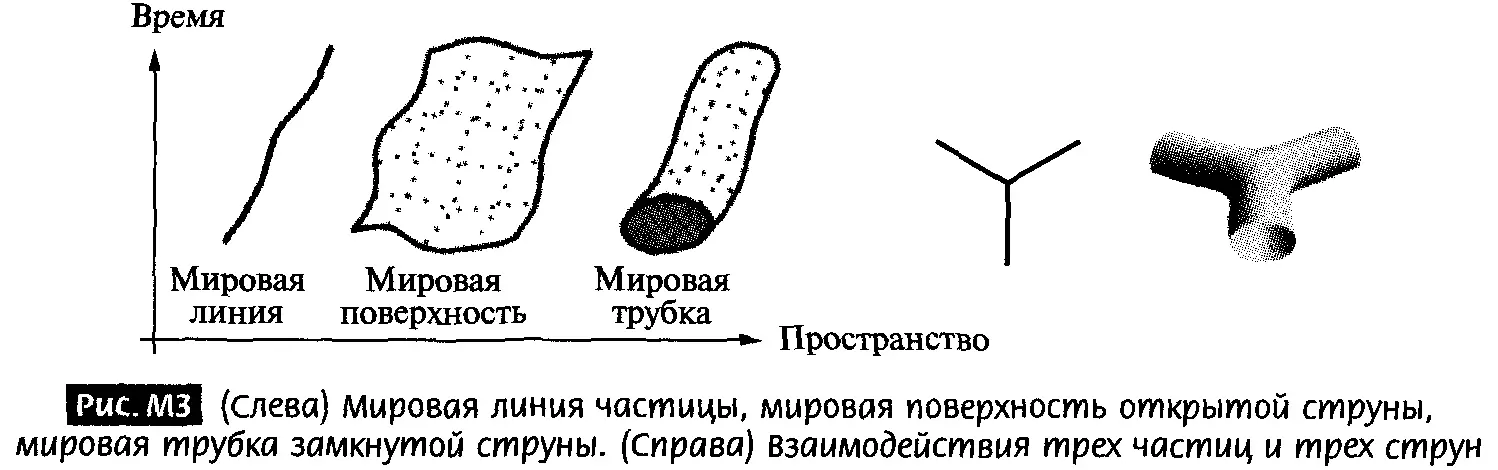
Небольшое отступление по теории струн и минимальным поверхностям: теория струн — это попытка описать все фундаментальные частицы и силы природы в рамках единой модели. В ней предполагается, что элементарные частицы — это не точки, а крошечные колеблющиеся струны. Хотя экспериментального подтверждения у теории пока нет, в ходе ее развития физики создали чрезвычайно мощный математический инструментарий.
Одним из ключевых объектов этой математики стали минимальные поверхности — формы, которые при заданных границах имеют наименьшую возможную площадь. Это поверхности, которые образуются в ходе движения тех самых струн. Если струна замкнута в окружность, то, двигаясь во времени, она заметает мировую поверхность — подобно тому как мыльная плёнка рождается из проволочного кольца.
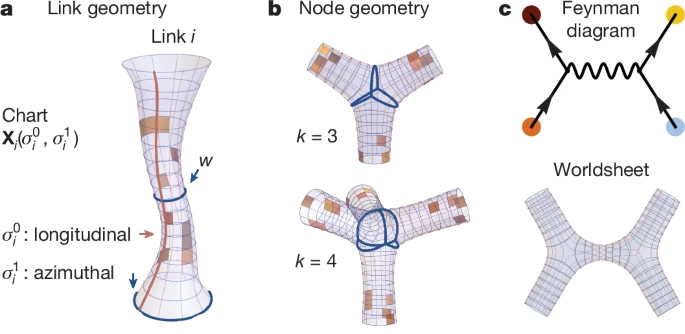
В новой работе, ученые показали, что формы биологических сетей почти идеально описываются уравнениями минимальных поверхностей, заимствованными из теории струн. То есть природа оптимизирует не длину, а площадь поверхности. Такой подход сразу объяснил то, что раньше считалось аномалиями: тройные и четверные узлы возникают естественно при соединении нескольких поверхностей; тонкие боковые отростки оказываются геометрически выгодными; почти перпендикулярные побеги минимизируют локальные напряжения поверхности.
Особенно выразительно это проявляется в нейронах мозга, где боковые отростки часто заканчиваются синапсами, а также в корнях растений, исследующих почву во всех направлениях с минимальными затратами ресурсов.
Чтобы проверить теорию, исследователи проанализировали высокоточные трехмерные сканы шести принципиально разных сетей: нейронов человека, нейронов плодовой мушки, кровеносных сосудов человека, тропических деревьев, кораллов, растения Arabidopsis thaliana. Во всех случаях реальная геометрия разветвлений лучше соответствовала принципу минимизации поверхности, чем классической модели минимальной длины.
Биологические системы, разумеется, не являются чистыми математическими объектами. На их форму влияют гены, механические нагрузки, химические сигналы и случайности развития. Поэтому они не достигают абсолютного геометрического идеала. Но, как подчеркивают авторы исследования, общий принцип остается универсальным: жизнь снова и снова подчиняется принципу минимальной энергии.
P.S. Есть в этой истории особая ирония. Теорию струн часто упрекали в оторванности от реальности. И вдруг именно ее математика помогает понять, почему нейроны, ветви и сосуды так похожи. Порой самые абстрактные идеи оказываются ключом к самым живым формам.
Больше интересного читай в моем Telegram канале.
Автор: Zarifa


