Введение
Одна из проблем при проектировании сверточных сетей (CNN) – несоответствие размеров тензоров. Неправильно заданные padding, stride или dilation могут замедлить разработку модели.
Этот туториал – шпаргалка по формулам расчета размерности преобразованного изображения. Мы разберем, как каждый параметр свертки влияет на ширину и высоту выходного тензора. Материал будет полезен как новичкам, так и опытным разработчикам, желающим освежить ключевые формулы.
Операция свертки
Пропустим вступление про то, что такое сверточный слой (подробнее можно посмотреть здесь). Скажем лишь, что это такой слой, который преобразует входное изображение, выделяя некоторые локальные свойства. Выделение тех или иных свойств зависит от ядра свертки. Ядро свертки – это тензор, который последовательно накладывается на разные участки входного изображения. На выходе, после применения ядра мы получаем новое преобразованное изображение. Чуть более формальней, свертка – математическая операция, которая по двум входным последовательностям выдает третью последовательность, которая показывает влияние этих двух последовательностей друг на друга.
Рассмотрим двумерное изображение , то есть матрицу размерности
, где
высота в пикселях, а
– ширина. Ядро обозначим через
. Будем предполагать, что
меньше размера изображения, чаще всего
или
. Тогда операцию свертки можно записать как
где . То есть для фиксированной пары пикселей
мы проходимся по квадрату, двигаясь при помощи индексов
. Если начинать нумерацию с нуля, то последняя позиция преобразованного изображения будет
, то есть мы возьмем последний пиксель
исходного изображения (граница изображения) и дальше уже двигаться не будем, поскольку изображение закончилось. Пиксели изображения
мы взвешиваем при помощи ядра
и суммируем результат. Схематично это выглядит следующим образом.
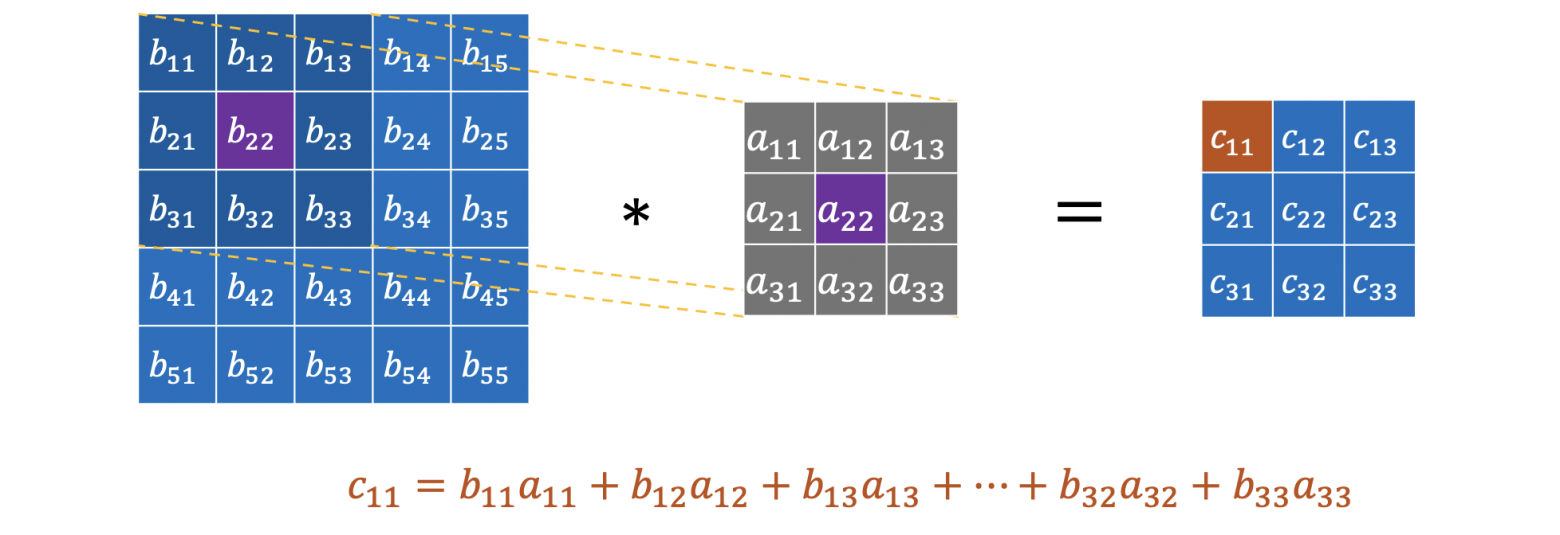
На самом деле это операция не свертки, а кросс-корреляции. В настоящей же свертки мы бы еще получили перевернутое изображение, что вообще говоря не удобно и несет иной смысл, но несмотря на это, термин свертка закрепился в литературе и используется в замен кросс-корреляции. Стоит также отметить, что в общем случае, ядро может быть не квадратным. Однако здесь мы рассмотрим случай именно квадратного ядра .
В случае, когда изображение состоит из каналов, то есть имеется тензор
, и мы хотим получить изображение из
каналов, необходимо использовать совокупность ядер
.
То есть, для каждого нового канала у нас отдельное ядро, которое в свою очередь применяется ко всем каналам исходного изображения. Количество каналов в ядре должно совпадать с количеством каналов в исходном изображении. На картинке ниже к изображению 5 на 5 с тремя каналами применяется два ядра 3 на 3 с тремя каналами и получается изображение 3 на 3 с двумя каналами.
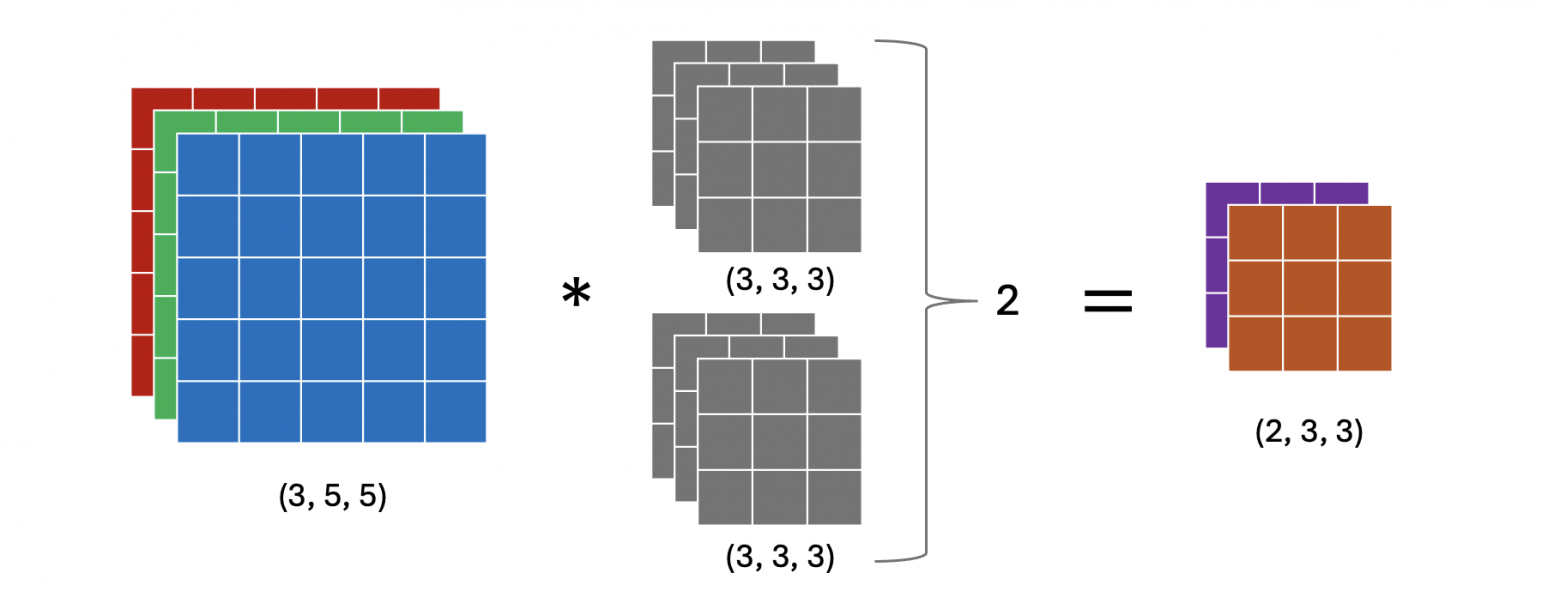
С учетом смещения (bias) мы получим финальную формулу
Давайте для удобства переобозначим входное количество каналов и выходное
. Тогда мы получим нашу первую полезную формулу – количество обучаемых параметров в одной свертки, которое равно
. Мы должны взять
ядер, каждое размера
, а затем прибавить вектор смещение, размерность которого есть выходное число каналов
.
Пример: преобразуем изображение с 3-х каналов до 64, тогда количество параметров будет равно .
Вычисление размера изображения без параметров
Давайте теперь разберем, как изменится размер изображения если применить к нему операцию свертки. Для начала рассмотрим самый простой случай, когда применяется обычное ядро размера . Также для упрощения мы рассмотрим только движение ядра по горизонтали, по вертикали будет тоже самое, все формулы останутся верны.
Сперва, мы ставим наше ядро в левый верхний угол – это стартовая позиция. Затем смещаем ядро до тех пор, пока оно не достигнет правой границы изображения. Дальше двигать ядро мы не можем (пока что). Соответственно, если мы стартовали с позиции (левый верхний угол), то конкретно в данном примере первый пиксель ядра встанет на позицию
.
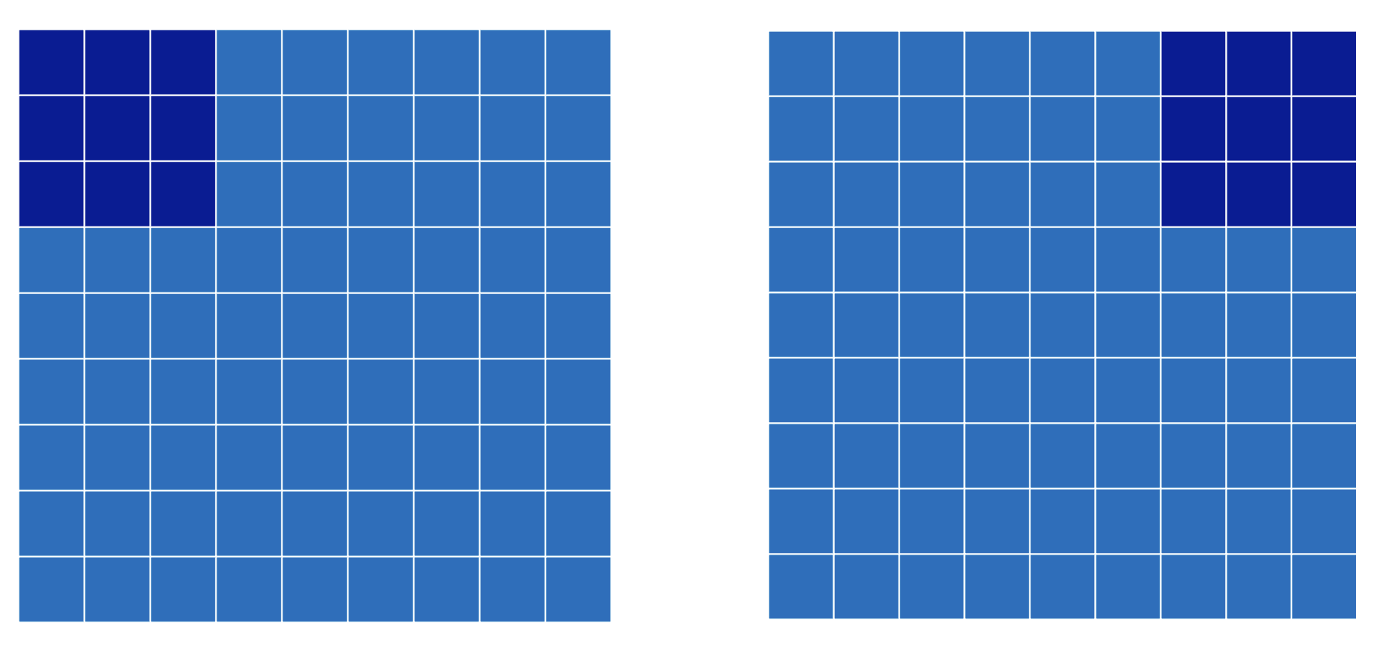
Именно семь позиций мы можем занять в случае ядра для изображения
. Не сложно увидеть закономерность. Всего позиций которые мы сможем занять не должно превышать ширину исходного изображения
, то есть
. То есть если мы на позиции
, то дальше может поместиться только
пиксель. Откуда можно получить равенство
, поскольку нас интересует максимально возможное число позиций. Максимальная позиция
и будет новая ширина
нашего преобразованного изображения.
Stride (шаг, смещение)
Перейдем к вычислению размера изображений с применением некоторых параметров свертки. Сперва разберем случай страйда (шаг). В классическом случае ядро шагает на каждый следующий пиксель, то есть по умолчанию . Если же мы хотим вычислять признаки не на каждом шаге, а через пиксель, то есть позиция ядра будет скакать на два пикселя, то страйд необходимо задать равным двум,
.
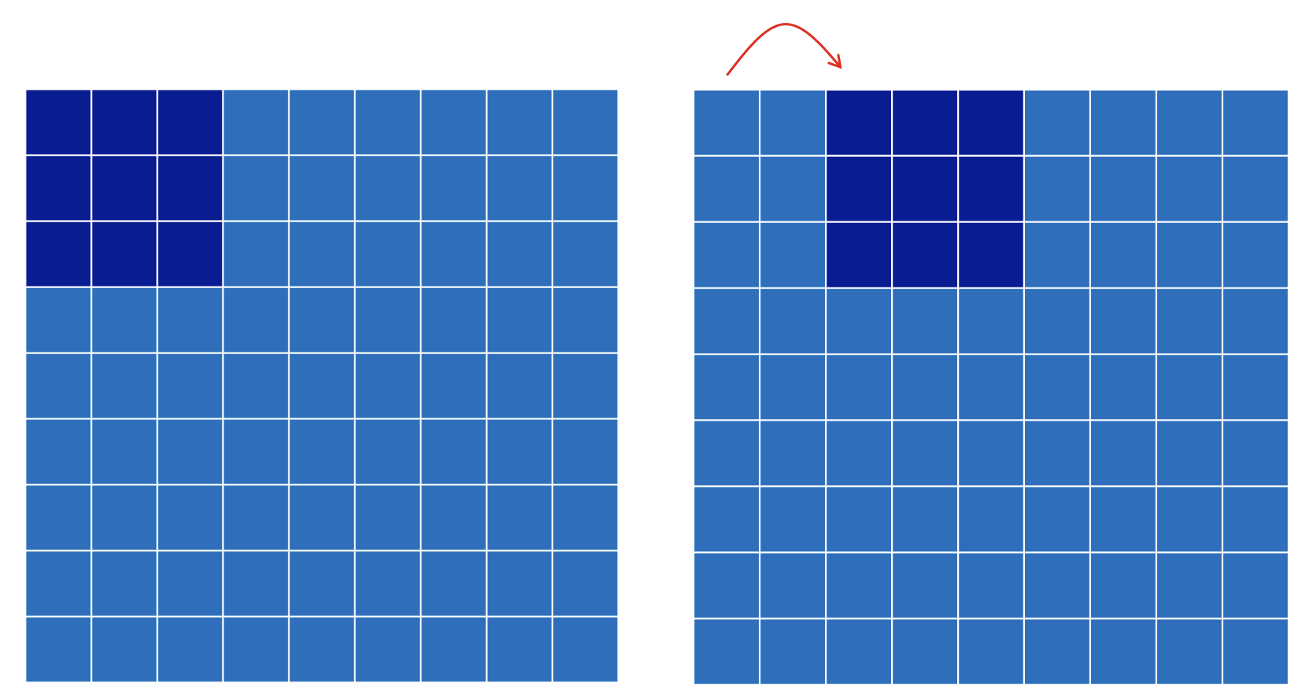
Рассмотрим опять наш случай с изображением и возьмем
. Тогда, ядро сможет прыгнуть только один раз, поскольку тут же достигнет правой границы исходного изображения. Наш индекс позиции ядра будет меняться как
. При
индексы будут
. Так как 13, уже за пределами нашего изображения, то этот шаг уже не выполняется.
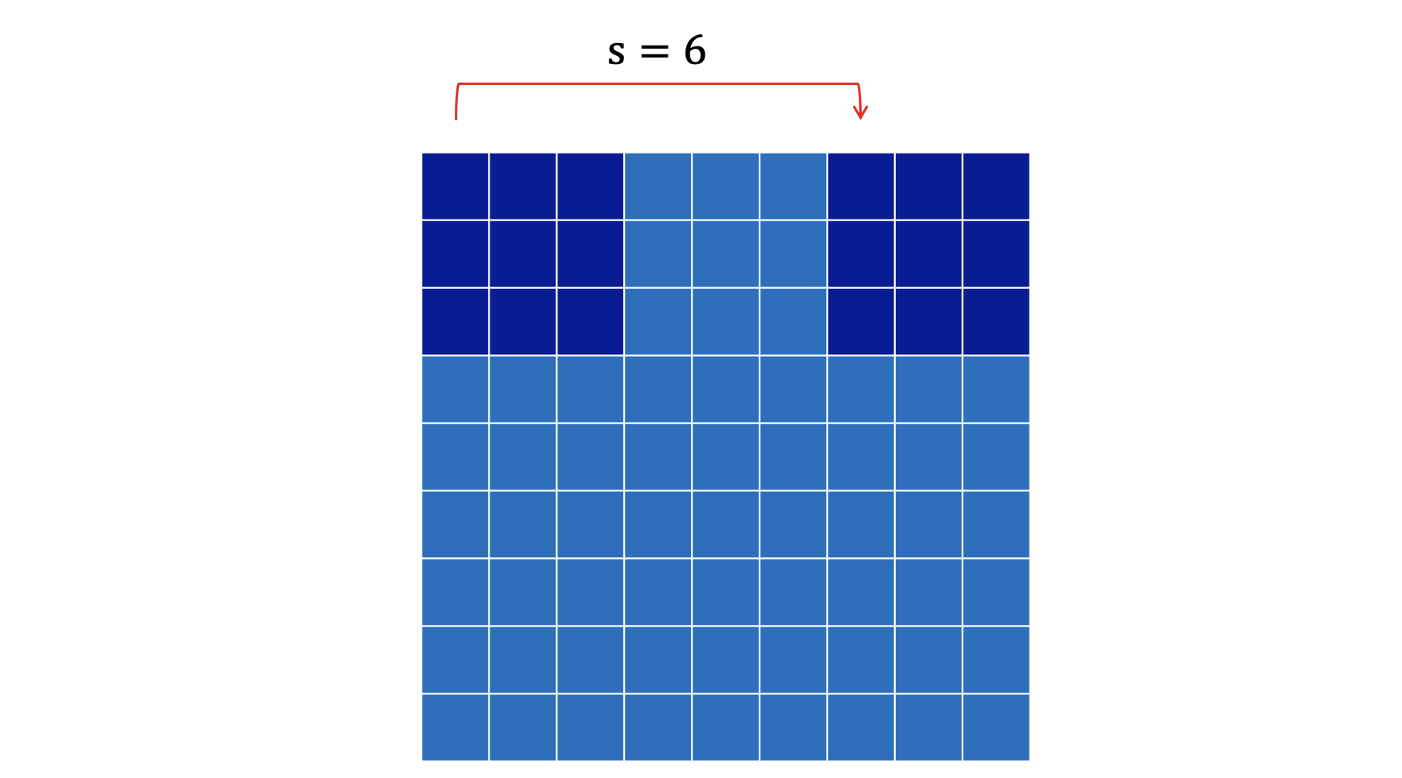
Из наблюдений выше можно понять, что общая формула для позиции ядра будет равна , где
некоторый множитель, который отвечает за то, сколько раз мы можем прыгнуть. Наша задача как раз определить како��
максимально возможен при размере изображения
.
Мы уже знаем, что должно выполняться условие . Давайте подставим наше выражение для
:
Нижняя граница берется лишь потому, что нам необходимо найти минимально возможный прыжок, поскольку следующий шаг будет за пределами изображения и конечно он должен быть целым числом.
Поскольку множитель менялся от нуля до
, то всего допустимых значений будет
. Финальная формула для вычисления размера преобразованного изображения с учетом страйда равна
Padding (дополнение, отступ)
Следующий параметр свертки называется дополнением или паддингом (padding). Здесь мы как раз возвращаемся к тому, что ядро не может двигаться дальше исходного размера изображения, поскольку просто нет возможных дополнительных пикселей. Однако часто, нам может быть интересно значение на границе изображения или же нам необходимо сохранить размер изображения не тронутым. Для этого можно использовать паддинг.
В классической свертки по умолчанию паддинг равен нулю, . По факту мы просто добавляем
пикселей с каждой стороны изображения. Таким образом, всего добавляется
пикселей,
пикселей слева и
пикселей справа. Аналогично, пиксели добавляются снизу и сверху. Конкретные значения добавленных пикселей не влияют на размер, обычно они просто равны нулю.
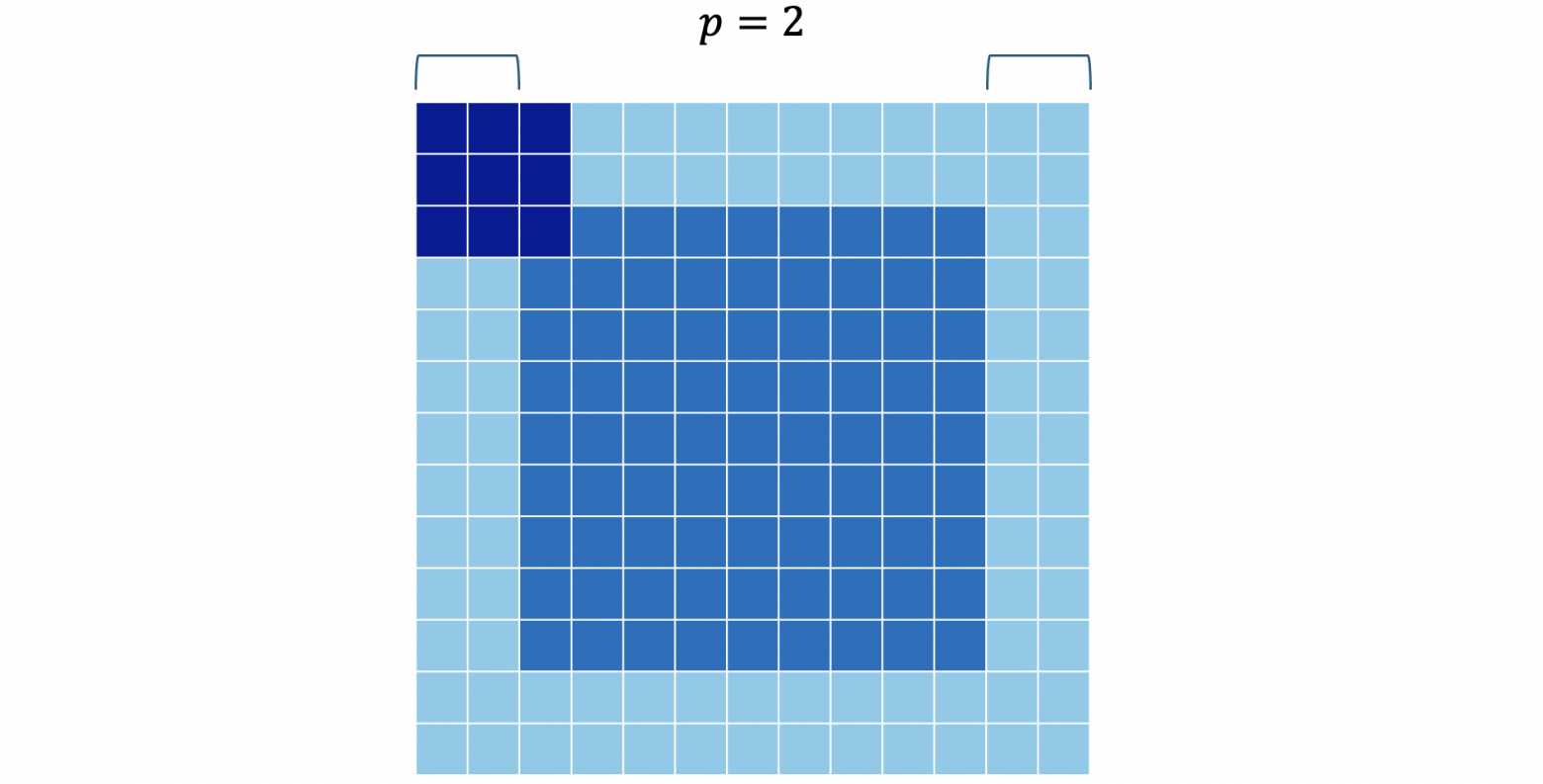
Итак, раз мы добавляем суммарно пикселей, то размер исходного изображения изменится на
. Откуда, сразу получим размер нового изображения с учетом паддинга
Dilation (дилатация, растяжение)
Последний параметр свертки который мы разберем называется дилатацией или растяжением (от англ. dilation). Дилатация позволяет растянуть ядро, то есть сделать его менее плотным. Например, когда мы не хотим смотреть только соседние пиксели, а хотим охватить более широкую область вокруг данных пикселей. По умолчанию, все пиксели ядра стоят рядом с друг другом, то есть дилатация равна 1, . На рисунке ниже, приведен пример с дилатацией равной трем, то есть между соседними пикселями ядра появился зазор в два пикселя.

Здесь нам понадобится новый термин – эффективный размер ядра, а именно размер области на изображении, которую покрывает ядро. Давайте найдем формулу для эффективного размера ядра.
Рассмотрим конкретный пример, когда ядро имеет размер и дилатация равна 3. Это означает, что между соседними пикселями ядра есть 2 пропуска. Обобщая, между соседними пикселями всегда
пропуск. Это следует просто из определения данного параметра.
Далее, давайте посмотрим сколько пикселей занимает ядро с дилатацией. Само ядро состоит из пикселей по горизонтали. В данном случае 3. А теперь посмотрим сколько у нас пропусков в ядре помещается. При ядре
, таких пропусков будет два, при ядре
таких пропусков будет 4, и так далее. Поэтому, для ядра
, всего
пропуск.
Итого, у нас есть пикселей ядра и
пропуск по
пикселю. То есть эффективный размер ядра равен
Возвращаясь к формуле со страйдом и паддингом, , заменим в ней размер ядра
на эффективный размер ядра
. Тогда, получим
.
Финальная формула со всеми тремя параметрами имеет вид
Как я говорил ранее, все те же самые вычисления верны и для движения ядра по вертикали, поэтому высота в пикселях будет вычисляться как
Заключение
Таким образом, мы рассмотрели с вами арифметику сверточных слоев и научились вычислять размер изображения ��осле применения операции свертки с учетом таких параметров, как страйд, паддинг и дилатация. Данные формулы будут вам полезны при композиции нескольких сверточных слоев, когда необходимо уравнивать размерности тензоров.
Еще больше интересного в моем тг канале, где я пишу про ИИ и не только.
Автор: kirillzx


